Sangat umum untuk merepresentasikan fungsi agar dapat menganalisis secara grafis hubungan antara berbagai variabel yang membentuk fungsi ini. Atau terkadang jenis representasi ini bahkan digunakan untuk membeli banyak fitur. Hal ini terutama digunakan ketika melakukan studi statistik. Karena itu, hari ini kami akan menjelaskan kepada Anda metode yang sangat sederhana yang hanya terdiri dari 3 langkah untuk membuat grafik fungsi apa pun. Selain itu, kami juga akan membahas cara menganalisis hasil grafis untuk menarik kesimpulan.
Jenis fungsi
Pertama, kita perlu memahami karakteristik berbagai jenis fungsi dan perbedaan apa yang harus dipertimbangkan saat merepresentasikannya. Dengan cara ini akan lebih mudah bagi kita untuk melakukan representasi grafis, oleh karena itu sekarang kami akan mengomentari secara singkat setiap jenisnya. Perlu dicatat bahwa ada banyak jenis fungsi, jadi kita akan fokus pada dua jenis fungsi polinomial dan fungsi piecewise yang paling penting.
fungsi linier
Fungsi linier atau fungsi polinomial derajat pertama adalah fungsi yang ekspresinya merupakan polinomial berderajat 1. Kemudian ekspresinya mengikuti model f(x) = mx + n , dengan m adalah kemiringan dan n adalah ordinatnya. Pada dasarnya fungsi-fungsi tersebut memiliki bentuk grafik yang setara dengan garis. Di bawah ini Anda dapat melihat contohnya:
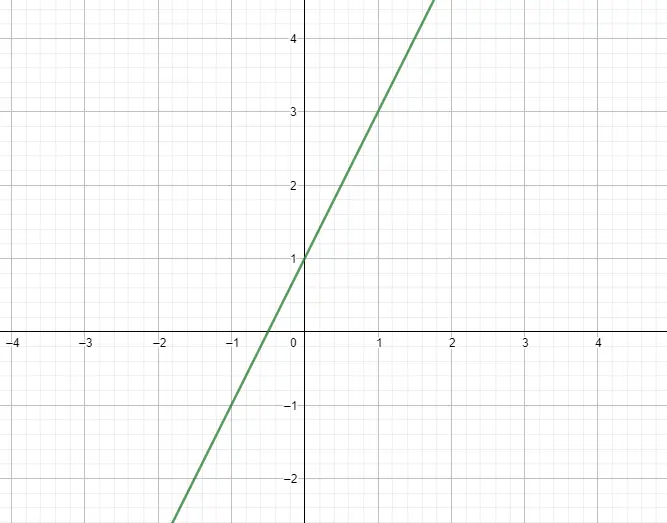
fungsi kuadrat
Fungsi kuadrat atau fungsi parabola dinyatakan dengan polinomial derajat kedua dan oleh karena itu berbentuk parabola. Sebagai model yang harus diikuti, kita akan memperhitungkan persamaan berikut: f(x) = ax² + bx + c, dengan a ≠ 0. Selain itu, ada dua karakteristik penting lainnya dari fungsi ini, amplitudo dan pertumbuhan. Di bawah ini Anda dapat melihat contohnya:
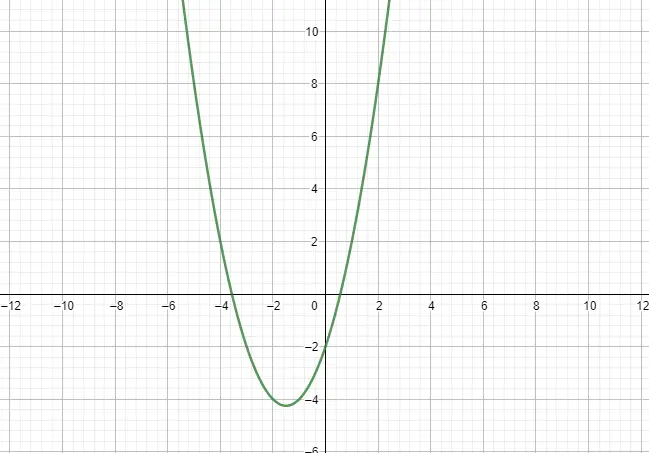
Fungsi sedikit demi sedikit
Fungsi terdefinisi sepotong-sepotong adalah fungsi yang definisinya berbeda-beda bergantung pada nilai x. Jadi ketika x menempati rentang nilai tertentu, kita perlu mencoba sebuah ekspresi. Sedangkan ketika x menempati nilai lain, ekspresi berbeda harus diproses. Di sinilah kita menemukan diskontinuitas dan juga batasan. Karena, ketika satu fungsi berakhir, fungsi lain dapat dimulai, tetapi tanpa menghubungkan secara langsung. Di bawah ini Anda dapat melihat contohnya:
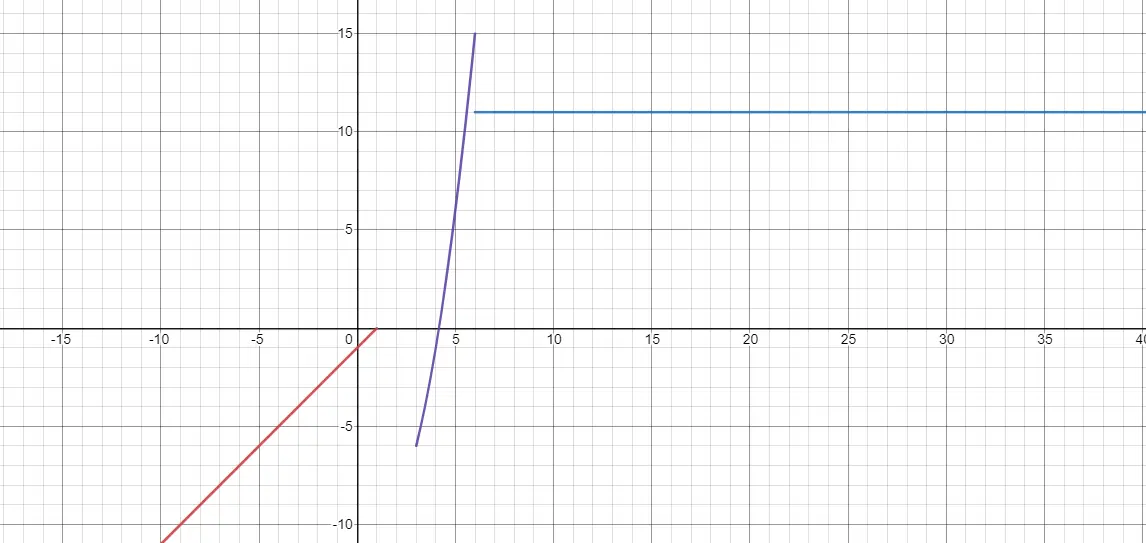
Bagaimana cara merepresentasikan fungsi linier?
Untuk membuat grafik fungsi linier, kita perlu mengikuti tiga langkah yang sangat sederhana. Selanjutnya kami akan menjelaskan prosedurnya, meskipun jika Anda ingin mempelajari cara membuat grafik fungsi parabola kami sarankan untuk membaca bagian selanjutnya.
Buat tabel nilai
Untuk dapat membuat grafik suatu fungsi, kita perlu membuat tabel nilai yang di dalamnya kita akan menuliskan semua nilai variabelnya. Pada dasarnya ini akan memungkinkan kita untuk membangun hubungan antara dua variabel dan dengan cara ini kita dapat menelusuri jalur fungsinya. Jika Anda belum mengetahui cara membuat tabel nilai, Anda dapat melihat tautan terakhir ini. Meskipun secara ringkas, ini terdiri dari memberi nilai pada variabel independen dan mensubstitusikan yang tidak diketahui ke dalam fungsi yang berhubungan dengannya. Jadi kita akan memiliki dua angka yang terkait, tabel berikut menunjukkan contohnya:
Dari fungsi f(x) = 2x+1:
| X | f(x) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
Gambarlah titik-titik pada grafik dan gabungkan dengan menggambar fungsinya
Setelah kita membuat tabelnya, kita bisa mulai menggambar titik-titik pada grafik. Kita melakukannya dengan mengasosiasikan variabel independen ke sumbu x dan variabel lainnya ke sumbu y, dan dengan cara ini kita akan mendapatkan poinnya. Anda dapat menggambar titik sebanyak yang Anda suka, meskipun untuk merepresentasikan fungsi gaya ini biasanya cukup menghitung lima poin. Sejak itu, mereka mengikuti jalan yang lurus dan, oleh karena itu, tetap sama tidak peduli seberapa jauh Anda maju.
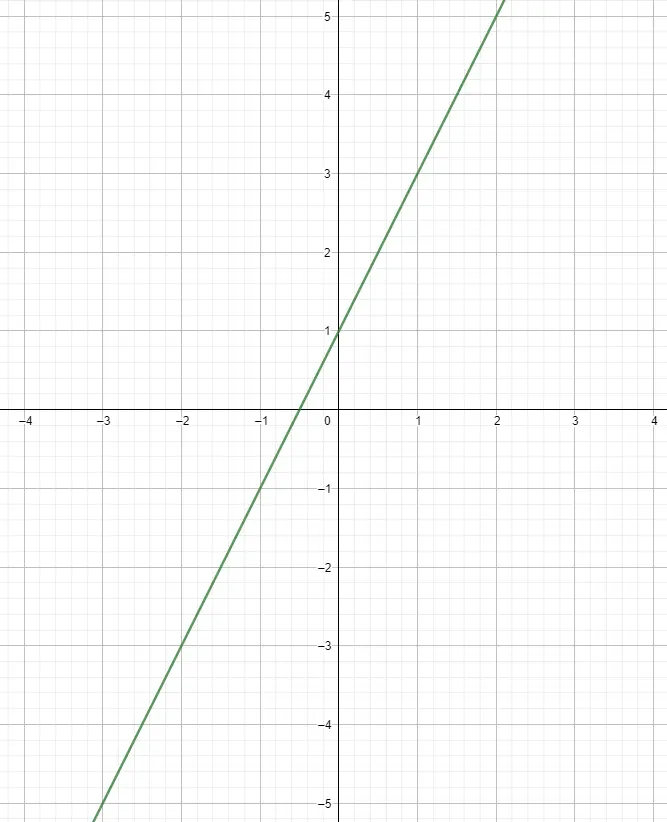
Menggunakan Kemiringan untuk Membuat Grafik Fungsi Linier
Ada metode kedua untuk dapat merepresentasikan fungsi linier secara grafis tanpa tabel nilai, yaitu dengan menghitung kemiringan fungsi: m = (variasi vertikal / variasi horizontal). Jadi setelah kita menghitung kemiringannya, kita perlu melihat titik awalnya. Kembali ke contoh sebelumnya f(x) = 2x+1, kita mengetahui bahwa titik awalnya adalah (0, 1), karena pada x = 0, komputer = 1 (kita menyimpulkannya dari +1 pada ekspresi) . Lalu tambahkan saja kemiringannya, yang dalam hal ini sama dengan +2 vertikal untuk 1 horizontal. Maka kita akan mengetahui bahwa poin selanjutnya adalah (1,3).
Bagaimana cara merepresentasikan fungsi kuadrat?
Untuk merepresentasikan fungsi kuadrat, kita dapat mengikuti dua metode, yang pertama melibatkan tabel nilai. Dan yang kedua terdiri dari menghitung serangkaian titik-titik penting: titik sudut, titik potong dengan sumbu X, dan titik potong dengan sumbu Y. Yang terakhir inilah yang akan kami jelaskan di bawah ini:
Hitung titik puncak parabola
Ada dua rumus yang memungkinkan kita menghitung titik puncak fungsi parabola, pada dasarnya rumus yang satu memberi kita titik puncak sumbu X dan rumus lainnya memberi kita titik puncak sumbu Y. Anda dapat menemukan kedua rumus di bawah, namun keduanya memiliki struktur yang serupa.
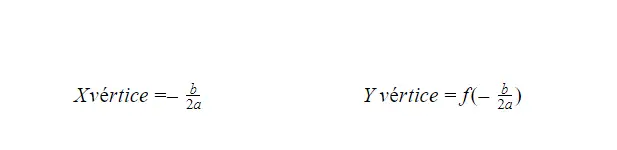
Hitung titik potong dengan sumbu X suatu fungsi kuadrat
Untuk mendapatkan titik potong dari persamaan tersebut, yang harus kita lakukan hanyalah menyelesaikan persamaan tersebut dan kita sudah mendapatkan nilai X yang kita cari. Perlu dicatat bahwa sebagai fungsi kuadrat kita akan mendapatkan dua hasil, bukan hanya satu.
Hitung titik potong dengan sumbu Y suatu fungsi kuadrat
Terakhir, untuk mendapatkan titik potong dengan sumbu Y, cukup hitung c = f(0). Dan karena parabola selalu memotong sumbu vertikal (ordinat) pada x = 0, maka titik potong sumbu Y adalah (0,c). Setelah kita memiliki semua titik tersebut, kita dapat menggambarnya pada grafik dan kita tinggal menggabungkannya dengan menggambar parabola seperti ini.
Bagaimana cara merepresentasikan fungsi secara sepotong-sepotong?
Untuk dapat merepresentasikan fungsi secara berkeping-keping, Anda dapat menggabungkan semua cara yang telah kami jelaskan sebelumnya. Karena fungsi gaya ini terdiri dari semua jenis fungsi yang kita bicarakan. Oleh karena itu, ada beberapa yang harus Anda hitung melalui tabel nilai dan ada pula yang harus Anda hitung dengan metode lain. Namun, setelah Anda menguasai apa yang telah kami jelaskan di artikel ini, Anda tidak akan lagi mengalami masalah saat merepresentasikan fungsi dalam beberapa bagian.
Di sisi lain, karena ketika mewakili mereka Anda harus melakukan studi kontinuitas, kami menyarankan Anda mempelajari cara mengatasi batasan tersebut , jika Anda belum mengetahui caranya. Ini akan membantu Anda merepresentasikan titik akhir setiap fungsi dengan benar. Karena itu, Anda kini siap membuat grafik fungsi sepotong-sepotong dan jenis fungsi lainnya juga. Kami sekarang meninggalkan Anda dengan serangkaian tip grafik dan penjelasan yang sangat berguna tentang kemampuan kalkulator untuk membuat grafik.
Bagaimana cara membuat grafik dengan kalkulator?
Jika Anda memiliki kalkulator grafik , ia akan memiliki kemampuan untuk membuat grafik. Hal ini bisa sangat mudah dilakukan setelah Anda mengetahui prosedurnya, namun jika Anda masih belum tahu cara melakukannya, sekarang kami akan menjelaskannya kepada Anda.
- Akses mode grafis: langkah pertama adalah mengakses opsi grafik atau representasi grafis dari menu. Opsi ini mungkin diberi label dengan nama berbeda untuk kalkulator Anda, namun opsi ini akan berisi kata-kata yang mirip dengan grafik atau kata-kata yang telah kita bicarakan.
- Sesuaikan opsi grafik: setelah kita berada di editor grafik, kita harus memberi nama pada file, memberi label pada sumbu, memilih jumlah elemen yang akan dibuat grafiknya, dan mengonfigurasi opsi estetika representasi. Ini adalah langkah yang sangat cepat untuk dilakukan.
- Tambahkan titik-titik fungsi: Anda kemudian dapat mulai menambahkan titik-titik yang akan membentuk gambar. Caranya dengan menuliskan titik-titik dengan notasi berikut: (0,1), (3,2)… Dan Anda akan terus menjumlahkan titik-titik tersebut hingga Anda menyelesaikan grafiknya.
- Gunakan fungsi “Pratinjau”: setelah Anda menyelesaikan proyek, Anda dapat melihat pratinjau hasilnya dan melihat apakah hasilnya sesuai yang diharapkan. Ditambah lagi, banyak templat yang memiliki opsi pengeditan dengan pratinjau ini, sehingga Anda dapat mengubah hasilnya hingga sempurna.
- Simpan proyek: Setelah seluruh prosedur pengeditan selesai, ingatlah untuk menyimpannya di lokasi yang mudah diingat. Dengan cara ini, kapan pun diperlukan, Anda dapat mengakses proyek lagi untuk melihatnya atau melakukan perbaikan yang diinginkan.
Kalkulator terbaik untuk merepresentasikan fungsi
Jika Anda tertarik untuk membeli model grafis agar dapat merepresentasikan fungsi pada kalkulator yang sama, kami merekomendasikan dua model: HP 50G dan HP Prime . Ini adalah dua model dengan kualitas terbaik, meskipun harganya mahal, jadi Anda perlu bertanya pada diri sendiri apakah investasi tersebut sepadan untuk Anda. Misalnya, jika Anda akan mempelajari karir seperti teknik yang sangat kompleks dari segi matematika, maka sangat disarankan untuk membeli salah satu dari dua model ini. Namun, jika Anda tidak membutuhkan banyak daya komputasi atau grafis, mungkin Casio FX-9750GII sudah cukup untuk Anda.
Bagaimana cara membuat grafik fungsi secara online?
Anda selalu dapat memilih opsi untuk menggunakan program grafis online, seperti: Desmos , Geogebra dan banyak lainnya. Dengan cara ini Anda akan mendapatkan grafik yang sangat akurat dengan cepat. Bentuk bilangan dapat dikatakan digunakan ketika ingin membuat grafik fungsi dengan mudah dan cepat. Di sisi lain, jika Anda ingin membuat grafik fungsi sehingga Anda dapat mengeditnya (mengubah semua atributnya) dan memiliki sumber daya analisis fungsi berkualitas tinggi di ujung jari Anda, kami sarankan untuk membeli kalkulator ilmiah.