Binomial Newton adalah rumus matematika yang digunakan untuk menyatakan jumlah dua suku yang dipangkatkan . Rumus ini, dinamai menurut nama ahli matematika Inggris Isaac Newton, digunakan di banyak bidang matematika.
Misalnya, ia mempunyai kegunaan dalam statistik, teori probabilitas, dan kalkulus diferensial dan integral. Teorema binomial memungkinkan kita menghitung pangkat binomial dengan cara yang sederhana.
Sederhananya, binomial Newton didasarkan pada rumus yang dapat menyelesaikan ekspresi aljabar apa pun dalam bentuk (a+b) n . Terlepas dari kenyataan bahwa rumus ini dinamai Isaac Newton, perlu disebutkan bahwa ada kontroversi mengenai asal usulnya.
Artinya, beberapa penelitian menyarankan penggunaan teorema binomial di Timur Tengah.
Kapan binomial Newton dikembangkan?
Teorema binomial Newton, juga dikenal sebagai binomial Newton, dikembangkan pada tahun 1665 dan pertama kali dikomunikasikan dalam dua surat dari pejabat Royal Society pada tahun 1676 .
Surat-surat ini merupakan tanggapan terhadap matematikawan Jerman Gottfried Wilhelm von Leibniz, yang berusaha untuk lebih memahami penyelidikan matematika terhadap deret tak hingga. Newton membagikan hasil teoremanya dan Leibniz mengakui bahwa itu adalah teknik yang berguna untuk memperoleh hasil dalam kuadrat atau deret.
Pengamatan ini memungkinkan Newton untuk menyimpulkan bahwa pengoperasian deret tak hingga dapat dilakukan dengan cara yang sama seperti ekspresi polinomial hingga . Meskipun Newton tidak pernah menerbitkan teoremanya, matematikawan Inggris John Wallis menerbitkannya dalam Aljabar pada tahun 1685 dan mengaitkan penciptaannya dengan Newton.
Mengapa disebut binomial Newton?
Nama binomial Newton diambil dari nama ahli matematika dan fisikawan Inggris Isaac Newton, yang mengembangkannya pada abad ke-17 . Newton bukanlah orang pertama yang menemukan teorema ini, namun ia adalah orang pertama yang membuktikan validitasnya untuk bilangan bulat positif n.
Binomial Newton adalah alat matematika yang sangat berguna dalam aljabar dan kalkulus, dan banyak digunakan dalam bidang-bidang seperti fisika, statistik, teknik, dan ilmu komputer.
Apa rumus binomial Newton?
Seperti yang kami sebutkan sebelumnya, binomial Newton adalah rumus yang dapat digunakan untuk mencari pangkat binomial . Untuk mencari pangkat binomial tersebut, digunakan “koefisien binomial”. Istilah sebelumnya mengacu pada urutan kombinasi.
Dengan mengingat hal ini, kita dapat menguraikan rumus binomial Newton sebagai berikut:
- (a + b) 2 = a 2 + 2ab + b 2
- (a – b) 2 = a 2 – 2ab + b 2
- (a + b) 3 = a 3 + 3a 2 b + 3 ab 2 + b 3
Ekspresi matematika yang mengacu pada perkembangan (a+b) n disebut entitas penting, dan memungkinkan diperolehnya rumus umum yang mewakili operasi ini untuk bilangan asli “n”.
Dengan memeriksa koefisien setiap polinomial yang dihasilkan, kita dapat melihat barisan yang mengikuti apa yang disebut Segitiga Pascal .
Barisan segitiga Pascal diawali dengan angka 1, dan pada setiap baris berikutnya angka akhirnya selalu 1. Nilai antara diperoleh dengan menjumlahkan dua angka dari baris sebelumnya yang berada tepat di atas nilai yang akan dihitung.
Bagaimana cara mencari suku dalam binomial Newton?
Untuk mencari suku tertentu dalam binomial Newton digunakan rumus umum:
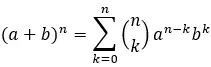
Emas:
a dan b adalah koefisien binomial.
n adalah eksponen binomial.
k adalah istilah spesifik yang ingin kita temukan.
Σ mewakili jumlah k=0 hingga n.
[nk] adalah koefisien binomial yang dihitung dengan rumus berikut:
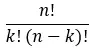
Oleh karena itu, rumus yang diperluas sepenuhnya adalah:
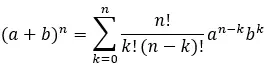
Contoh binomial Newton terselesaikan
Setelah nilai-nilai ini ditemukan, nilai-nilai tersebut disubstitusikan ke dalam rumus dan ekspresi diselesaikan untuk mendapatkan suku tertentu. Misalnya, jika kita ingin mencari suku kelima binomial (2x + 3) 6 , kita akan mendapatkan:
satu = 2x
b = 3
n=6
k = 5
Jadi, menggunakan rumus:
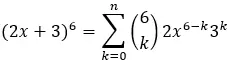
Suku kelima berhubungan dengan k=5, oleh karena itu kita mempunyai:
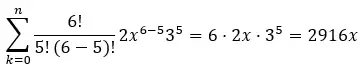
Jadi suku kelima binomial (2x + 3) 6 adalah 2916x.
Apa yang dimaksud dengan binomial Newton derajat 5?
Binomial Newton derajat 5 adalah ekspresi aljabar dalam bentuk (a + b) 5 , di mana “a” dan “b” adalah variabel dan eksponen 5 menunjukkan derajat binomial tersebut . Memperluas ekspresi ini, kita memperoleh polinomial kuadrat yang memiliki enam suku:
(a + b) 5 = a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5
Setiap suku polinomial ini diperoleh dengan menggabungkan koefisien binomial dengan pangkat “a” dan “b”. Misalnya, suku kedua (5a 4 b) diperoleh dengan mengalikan koefisien binomial (5 pilih 1 = 5) dengan “a” dipangkatkan keempat dan b dipangkatkan pertama.
Binomial Newton derajat 5 berguna dalam berbagai cabang matematika dan fisika, seperti statistik, teori probabilitas, dan mekanika kuantum.
Apa penerapan binomial Newton?
Binomial Newton memiliki beragam penerapan di berbagai bidang, antara lain:
- Menghitung probabilitas : Teorema binomial digunakan untuk menghitung probabilitas kejadian binomial, seperti pelemparan koin atau keberhasilan atau kegagalan serangkaian tes.
- Teori Bilangan – Binomial Newton digunakan untuk memperluas polinomial dan menyederhanakan persamaan dalam teori bilangan.
- Statistik : Binomial Newton digunakan untuk menghitung distribusi binomial dan membangun interval kepercayaan.
- Fisika – Dalam fisika, teorema binomial digunakan antara lain dalam teori relativitas dan mekanika kuantum.
- Ekonomi dan Keuangan : Binomial Newton digunakan untuk menghitung nilai arus kas saat ini dan masa depan dari waktu ke waktu dan dalam penilaian opsi keuangan.
- Pemrograman dan ilmu komputer : Binomial Newton digunakan dalam pengembangan algoritma dan pemrograman komputer.
Mengapa binomial Newton penting?
Binomial Newton relevan karena merupakan alat matematika mendasar untuk pengembangan aljabar dan teori bilangan . Ini memungkinkan Anda menghitung hasil kuadrat atau pangkat binomial lainnya, yang sangat berguna untuk menyelesaikan persamaan dan menyederhanakan ekspresi aljabar.
Selain itu, ia memiliki aplikasi di berbagai bidang seperti statistik, probabilitas dan fisika , antara lain. Singkatnya, binomial Newton adalah konsep penting dalam matematika dan pemahamannya sangat penting untuk kemajuan dalam banyak bidang studi.
Apakah ada cara lain untuk menyatakan binomial Newton?
Ya, ada cara lain untuk menyatakan binomial Newton. Misalnya, dapat dinyatakan dalam koefisien binomial menggunakan notasi kombinatorial.
Selain itu, dapat dinyatakan dalam fungsi eksponensial dan fungsi trigonometri menggunakan rumus Euler. Begitu pula dari segi fungsi gamma menggunakan rumus Legendre. Ekspresi alternatif ini dapat berguna dalam konteks dan masalah matematika yang berbeda.
Contoh Binomial Newton
Mari kita lihat beberapa contoh sederhana penerapan binomial Newton.
Contoh 1: Hitung suku orde 3 pada perluasan (x + y) 5 .
Penyelesaian: Pada perluasan (x + y) 5 , koefisien suku pertama adalah 1, koefisien suku kedua adalah 5, koefisien suku ketiga adalah 10, koefisien suku keempat adalah 10, koefisien suku keempat adalah 10, koefisien suku kelima adalah 5 dan koefisien suku keenam adalah 1.
Oleh karena itu, suku orde 3 adalah:
10x 2 dan 3
Contoh 2: Tentukan suku bebas pada perluasan (2x – 1) 4 .
Penyelesaian: Pada perluasan (2x – 1) 4 , suku bebasnya terdapat pada kombinasi (2x) p (-1) (4-p) , dengan p adalah nilai yang menjadikan pangkat dari (2x) p dan (-1) (4-p) dijumlahkan menjadi 4.
Oleh karena itu, istilah independennya adalah:
(2x) 2 (-1) 2 = 4
Contoh 3: Tentukan suku derajat tertinggi pada perluasan (3x – 2y) 6 .
Penyelesaian: Suku pangkat tertinggi pada perluasan (3x – 2y) 6 terdapat pada kombinasi (3x) p (-2y) (6-p) , dimana p adalah nilai yang menjadikan pangkat dari (3x) p dan (-2y) (6-p) sama dengan derajat binomialnya, yaitu 6.
Oleh karena itu, istilah derajat tertinggi adalah:
(3x) 3 (-2y) 3 = -216x 3 dan 3