Binomial - Mathoritas

Di halaman ini Anda akan menemukan penjelasan tentang apa itu binomial dan selain itu Anda juga dapat melihat contoh masing-masing jenis binomial. Kami juga menunjukkan rumus yang digunakan untuk menyelesaikan operasi binomial: perkalian binomial, kuadrat binomial, pangkat tiga binomial,…

Apa itu pasangan?

Dalam aljabar, definisi binomial adalah:

Binomial adalah polinomial yang hanya terdiri dari dua monomial . Dengan kata lain, binomial terdiri dari ekspresi aljabar yang hanya terdiri dari 2 suku berbeda yang digabungkan dengan tanda plus (+) atau tanda minus (-).

Kata binomial berasal dari bahasa Yunani dan terdiri dari dua komponen leksikal ( bi dan nomos ), yang artinya sebagai berikut:

bi : arti awalan 2.
nomos : artinya bagian.

Oleh karena itu kita dapat menyimpulkan arti binomial: polinomial dengan dua bagian (atau 2 monomial).

Di sisi lain, konsep berpasangan mempunyai arti lain selain makna matematis, yaitu bahwa berpasangan juga dapat menunjuk pada sekumpulan dua kepribadian yang mempunyai peran utama dalam kehidupan politik, dalam disiplin olahraga tertentu atau bahkan dalam dunia hiburan. . Namun yang jelas, di sini kita akan fokus pada definisi matematis binomial.

Contoh binomial

Untuk menyelesaikan pemahaman tentang pengertian binomial, kita akan melihat beberapa contoh polinomial jenis ini:

Contoh binomial kuadrat:

$x^2+4x$

Contoh binomial derajat ketiga:

$x^3+5$

Contoh binomial derajat keempat:

$3x^4+8x^2$

Sekarang setelah kita mengetahui apa itu binomial, kita akan melihat berbagai jenis binomial yang ada dan cara penyelesaian operasi dengan binomial.

kuadrat binomial

Binomial kuadrat adalah identitas luar biasa, disebut juga produk luar biasa atau persamaan luar biasa. Menyelesaikan pangkat binomial yang dipangkatkan menjadi 2 bergantung pada apakah binomial tersebut merupakan binomial penjumlahan atau binomial selisih.

Binomial jumlah mengacu pada binomial yang kedua sukunya positif, artinya binomial jumlah kuadrat adalah:

$(a+b)^2$

Sebaliknya, binomial selisih (atau pengurangan) adalah konjugasi dari binomial penjumlahan, artinya salah satu monomialnya bertanda negatif. Oleh karena itu, ekspresi aljabar untuk selisih binomial kuadrat adalah:

$(a-b)^2$

Untuk menghitung binomial kuadrat, Anda harus menerapkan rumus yang, seperti telah kita lihat, bervariasi bergantung pada penjumlahan atau pengurangan. Cari tahu bagaimana hal ini dilakukan dalam rumus persamaan penting , di mana Anda dapat melihat semua penjelasan langkah demi langkah serta contoh dan latihan yang diselesaikan, dan bukan hanya 2 persamaan penting ini tetapi juga semuanya.

binomial potong dadu

Meskipun lebih jarang digunakan, binomial kubus juga dianggap sebagai produk terkenal. Atau dengan kata lain, ada aturan matematika yang memungkinkan Anda menemukan pangkat tiga binomial dengan cepat (Anda dapat melihatnya di tautan di atas untuk rumus identitas terkenal ).

Seperti sebelumnya, hasil potensiasi ini bergantung pada apakah ia merupakan pangkat tiga dari suatu penjumlahan:

$(a+b)^3$

Atau jika, sebaliknya, pangkatnya didasari oleh pangkat tiga selisih atau pengurangan:

$(a-b)^3$

Logikanya, perbedaan utama antara binomial kuadrat dan binomial pangkat tiga adalah eksponen pangkatnya. Namun, rumus binomial pangkat tiga jauh lebih rumit dibandingkan rumus binomial kuadrat.

perjanjian penting

Ada jenis binomial tertentu yang agak khusus karena karakteristiknya, karena binomial tersebut berhubungan dengan identitas terkenal (atau produk terkenal) yang kurang dikenal.

Jumlah kuadrat:
$a^2+b^2$
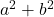
Selisih (atau pengurangan) kuadrat:
$a^2-b^2$
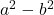
Jumlah kubus:
$a^3+b^3$
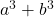
Selisih (atau pengurangan) kubus:
$a^3-b^3$

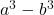
Emas

$a$

Dan

$b$

adalah dua monomial.

Meskipun ekspresi binomial ini sangat mirip dengan yang kita lihat di atas (binomial kuadrat dan binomial pangkat tiga), jika Anda perhatikan lebih dekat keduanya berbeda. Dalam pengertian ini, Anda juga dapat melihat rumus binomial terkenal dan pengurangannya dengan mengklik tautan di atas ⬆ rumus identitas terkenal.⬆

perkalian binomial

Salah satu operasi binomial yang paling umum adalah perkalian. Nah selanjutnya kita akan melihat contoh cara menghitung perkalian antar binomial.

$(x^2+2x)\cdot (x-5)$

Untuk menghitung perkalian binomial, pertama-tama kita harus mengalikan setiap suku pada binomial pertama dengan setiap suku pada binomial kedua:

$x^2\cdot x+x^2\cdot (-5)+2x\cdot x +2x\cdot (-5)$

$x^3-5x^2+2x^2 -10x$

Selanjutnya, kita mengelompokkan istilah-istilah serupa, yaitu istilah-istilah tersebut memiliki bagian literal yang sama:

$\bm{x^3-3x^2 -10x}$

Dan dengan cara ini kami berhasil menemukan hasil perkalian antar pasangan.

Hasil kali dua binomial dengan suku yang sama

Jika binomial yang ikut dalam perkalian memiliki suku yang sama dengan variabelnya

$x,$

Ada rumus untuk menghitung operasi binomial ini dengan cepat:

$(x+a)(x+b) = x^2+(a+b)x+ab$

Di sini kami tunjukkan latihan yang terselesaikan sehingga Anda dapat melihat cara menerapkan rumus ini:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

binomial Newton

Binomial Newton , juga disebut teorema binomial, adalah rumus yang digunakan untuk menghitung pangkat binomial.

Rumus matematika binomial Newton adalah sebagai berikut:

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}x^{n-k}y^k$

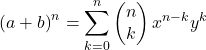
Atau setara:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

Seperti yang Anda lihat, rumus ini agak rumit untuk dipahami. Inilah sebabnya kami membuat pangkat binomial dengan derajat terendah di bawah ini agar Anda dapat memahaminya dengan lebih baik:

Rumus ini mungkin agak membosankan untuk menghitung binomial kuadrat atau pangkat tiga, karena seperti yang kita lihat di atas, ada rumus yang lebih sederhana. Namun binomial Newton sangat berguna untuk mencari pangkat yang derajatnya lebih tinggi, misalnya banyak digunakan untuk menentukan binomial ke empat.

Namun untuk menerapkan rumus ini, Anda harus mengetahui cara menghitung bilangan kombinatorial, yaitu ekspresi aljabar dari tipenya

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

, perhitungannya tidak mudah. 🔍 Inilah sebabnya kami menyarankan Anda mencari cara melakukannya di mesin pencari kami di kanan atas 🔎, Anda akan menemukan artikel kami di mana kami menjelaskan operasi ini kepada Anda langkah demi langkah.