Anda mungkin pernah mendengar tentang bilangan kompleks . Mereka mungkin merupakan kumpulan angka yang paling sulit untuk ditangani, karena mereka menggabungkan angka nyata dan imajiner. Penyatuannya memungkinkan untuk mempelajari perilaku numerik yang tidak dapat ditangani dengan menggunakan semua bilangan real.
Apa itu bilangan kompleks?
Bilangan kompleks adalah gabungan bilangan riil dan bilangan imajiner . Misalnya, 4 + 5i adalah bilangan kompleks yang mempunyai bagian real sama dengan 4 dan bagian imajiner sama dengan 5i. Secara umum kita dapat menyatakannya dengan rumus berikut:
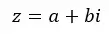
Dimana Re(z) = a dan Im(z) = b
Seperti yang telah kami katakan, kompleks adalah himpunan terbesar atau himpunan global , yang mencakup bilangan real dan bilangan imajiner. Selanjutnya, kami tunjukkan diagram kecil struktur hierarki semua himpunan:

Oleh karena itu, jika kita mempunyai kombinasi bilangan real dan bilangan imajiner, kita mempunyai bilangan kompleks. Namun, ada kalanya salah satu dari dua bagian tersebut sama dengan nol. Apa yang terjadi dalam kasus ini? Ya, kita masih berurusan dengan kompleks, karena himpunan kompleks mencakup semua himpunan numerik lainnya. Namun, kami memasukkan subkategori lain:
| bilangan kompleks | pesta kerajaan | bagian imajinasi | Subkategori |
| 2+5i | 2 | 5i | Kompleks |
| 4 | 4 | 0 | kerajaan murni |
| 3i | 0 | 3i | Imajinasi Murni |
Jika kita mempunyai bilangan real murni, karena nilai imajiner b sama dengan nol, bilangan kompleks yang tersisa ekuivalen dengan:
z = a + 0i = a
Sebaliknya, jika kita mempunyai imajinasi murni, a sama dengan nol dan, akibatnya, bilangan kompleksnya tetap sebagai berikut:
z = 0 + dua = dua
Representasi grafis dari bilangan kompleks
Untuk merepresentasikan bilangan kompleks, kita menggunakan bidang kompleks . Yang terdiri dari dua garis yaitu garis nyata dan garis khayal. Kedua garis bilangan ini digunakan untuk menemukan secara grafis angka-angka dalam setiap himpunan dan jika kita menggabungkannya, kita memperoleh sebuah rencana, seperti:

Sumbu X disebut sumbu nyata karena disitulah letak nilai bagian sebenarnya. Sedangkan sumbu Y disebut sumbu imajiner, di sinilah nilai imajiner ditulis. Mari kita lihat contohnya, kita akan menempatkan bilangan 3 + 2i pada bidang kompleks.

Seperti yang Anda lihat pada gambar, kami menemukan nomor tersebut menggunakan angka 3 dan 2 sebagai koordinat, masing-masing sebagai sumbu. Jika Anda ingin mempelajari lebih lanjut tentang merepresentasikan bilangan kompleks, kami sarankan membaca artikel ini.
Apa saja jenis-jenis bilangan kompleks?
Sekarang kita akan melihat cara kita menyatakan bilangan kompleks. Selama ini kita hanya melihat bentuk dasarnya (disebut bentuk binomial), yang ditulis sebagai penjumlahan: bagian real ditambah bagian imajiner.
Namun kenyataannya, kita memiliki tiga bentuk: binomial, polar, dan trigonometri . Setiap jenis ekspresi memiliki propertinya sendiri dan digunakan dalam situasi tertentu. Jadi kami akan menjelaskan semuanya dan menunjukkan cara berpindah dari satu ke yang lain.
1. Bentuk binomial
Bilangan kompleks dalam bentuk binomial dituliskan sebagai penjumlahan bagian real dan bagian imajiner: a + bi. Misalnya bilangan 6 + i merupakan bilangan kompleks yang dinyatakan dalam notasi binomial. Dalam hal ini, rumusnya selalu sama:

Oleh karena itu, untuk menyatakan bilangan kompleks dalam bentuk binomial, Anda hanya perlu mengetahui nilai sebenarnya dan nilai imajinernya.
Misalnya, nilai 3 + 2i berbentuk binomial dan, seperti yang kita lihat sebelumnya, direpresentasikan sebagai berikut:

Bentuk binomial terutama digunakan untuk menyelesaikan penjumlahan dan pengurangan bilangan kompleks.
2. Bentuk kutub
Untuk menyatakan bilangan kompleks dalam bentuk polar , kita harus menghitung modulnya |z| dan argumennya. Bentuk polar terutama digunakan ketika kita perlu menyelesaikan perkalian dan pembagian bilangan kompleks.
Untuk menghitung modulus bilangan kompleks, cukup lakukan modulus a dan b, seperti dijelaskan pada rumus berikut:

Dan untuk menghitung argumen atau sudut z, kita perlu menghitung garis singgung busur b antara a:

Penting untuk diperhatikan bahwa untuk menentukan secara tepat nilai sudut α, perlu diketahui di kuadran mana letaknya. Memang benar, fungsi tangen busur hanya menghitung sudut antara π/2 dan -π/2. Untuk menentukan di kuadran mana bilangan kompleks berada, kita harus melihat nilai a dan b (jika positif atau negatif):
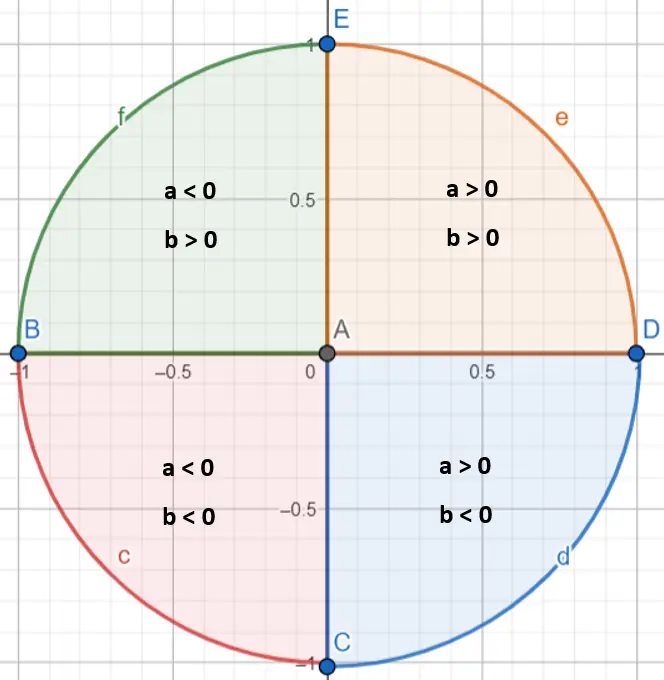
Setelah kita mengetahui di kuadran mana angka kita berada, kita perlu mengikuti beberapa aturan:
- Jika bilangan kompleks berada di kuadran pertama (a > 0 dan b > 0), argumennya akan dibiarkan apa adanya.
- Jika bilangan kompleks berada di kuadran kedua (a < 0 dan b > 0), kita akan menambahkan π ke argumennya.
- Jika bilangan kompleks berada di kuadran ketiga (a < 0 dan b < 0), kita kurangi π dari argumennya.
- Jika bilangan kompleks berada di kuadran keempat (a > 0 dan b < 0), kita akan menambahkan 2π pada argumennya.
Jika Anda tidak tahu apa yang kami bicarakan ketika kami mengatakan kuadran, kami menyarankan Anda untuk membaca artikel kami tentang rasio trigonometri .
Setelah kita mengetahui besaran dan argumen z, kita dapat menyatakan bilangan kompleks dalam bentuk polar. Meskipun formulir ini mempunyai beberapa nomenklatur, dua nomenklatur utamanya adalah:

Misalnya kita ingin mengubah bilangan 3 + 5i menjadi polar, kita cukup mengikuti prosedur berikut ini.
Kita hitung dulu modulnya:
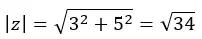
Lalu kita hitung argumennya yang ada di kuadran pertama, jadi tetap seperti yang kita hitung.
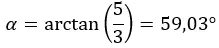
Dan kami menyatakan bilangan tersebut dalam bentuk kutub:
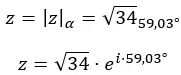
Representasi grafisnya adalah sebagai berikut:
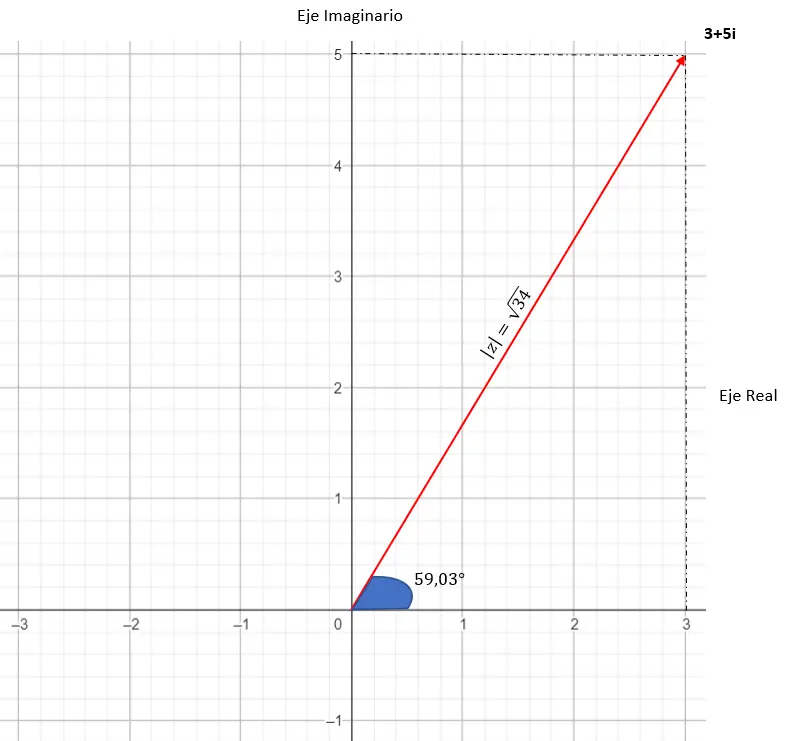
3. Bentuk trigonometri
Terakhir, kita memiliki notasi trigonometri , yang dihitung dari rumus Euler :

Misalnya untuk menyatakan bilangan 4 – 3i dalam bentuk trigonometri, kita mengikuti prosedur berikut:
Kita mulai dengan menghitung modulus dan argumen dengan rumus yang kita gunakan di bagian bentuk polar.
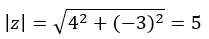
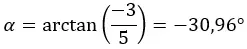
PERHATIAN : Argumen tersebut berada pada kuadran keempat, karena (a > 0 dan b < 0).
Kami menambahkan data ke dalam persamaan dalam bentuk trigonometri.
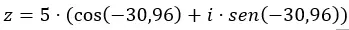
Dan kita sudah memiliki bilangan yang dinyatakan dalam bentuk trigonometri. Representasi grafisnya adalah sebagai berikut.
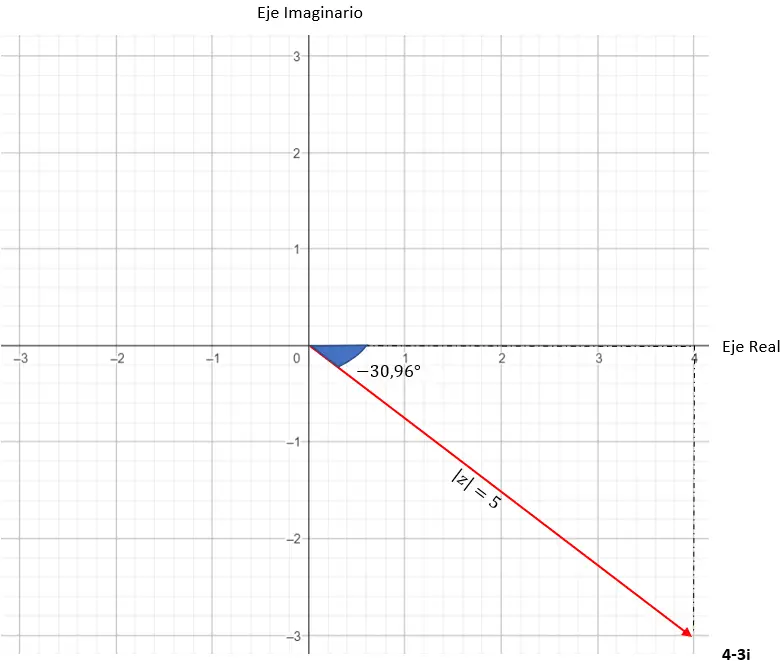
Bagaimana cara beralih dari satu tipe ke tipe lainnya?
Anda sekarang mengetahui semua cara untuk menyatakan bilangan kompleks. Dan sepanjang bagian terakhir Anda dapat melihat cara mengakses masing-masing formulir, namun sebelum kami menyelesaikannya, kami ingin memberikan ringkasan singkat tentang cara berpindah dari satu formulir ke formulir lainnya. Hanya Anda yang harus menggunakan rumus yang kita lihat di bagian sebelumnya.
Dari bentuk binomial ke polar dan sebaliknya
Untuk beralih dari binomial ke polar, kami mengusulkan diagram berikut:
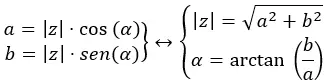
Kita telah melihat contoh sebelumnya dimana kita beralih dari binomial ke polar, jadi sekarang kita akan beralih dari polar ke binomial menggunakan diagram di atas. Kita perlu mengubah √41 38,66 menjadi binomial.
Kita hitung dulu a.
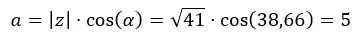
Lalu kita hitung b.
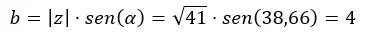
Dan kami menyatakannya dalam bentuk binomial.
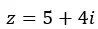
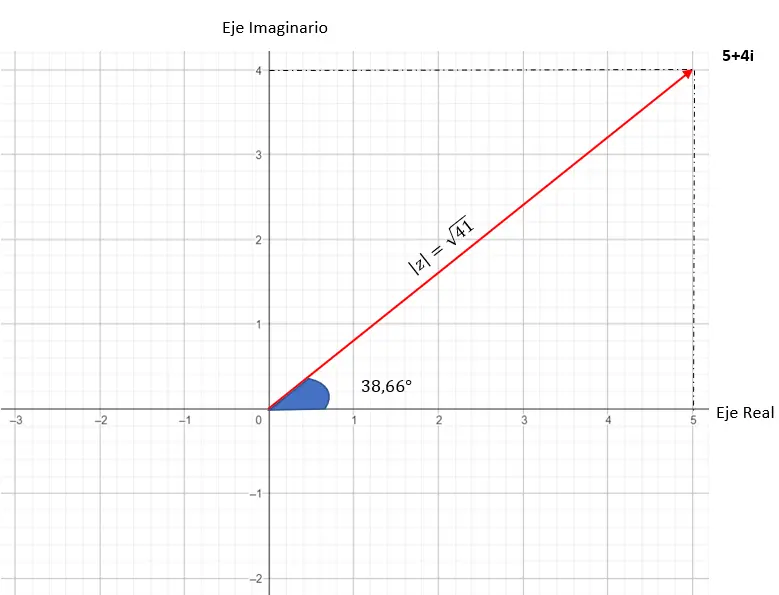
Representasi grafis dari angka ini terlihat seperti ini:
Dari bentuk binomial ke bentuk trigonometri dan sebaliknya
Untuk beralih dari binomial ke trigonometri, Anda juga harus menerapkan rumus yang telah kita bahas di bagian sebelumnya. Dengan cara ini, kita hitung dulu modulus dan argumennya, lalu kita masukkan datanya ke dalam persamaan bentuk trigonometri. Sebagai contoh, kita akan melewatkan bilangan z = 3 + 2i secara trigonometri.
Pertama-tama kita menghitung modulus dan argumennya.
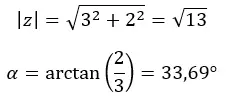
PERHATIAN : Argumennya berada pada kuadran I, karena (a > 0 dan b > 0).
Kemudian kita lengkapi persamaan bentuk trigonometrinya dengan data ini.
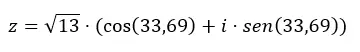
Dan jika kita ingin beralih dari trigonometri ke binomial, yang harus kita lakukan hanyalah menyelesaikan persamaan sebelumnya.
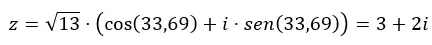
Dari bentuk polar ke bentuk trigonometri dan sebaliknya
Terakhir, kita akan beralih dari bentuk polar ke bentuk trigonometri. Ini cukup sederhana, karena kedua bentuk ini dinyatakan dengan dua nilai yang sama: modulo dan argument . Jadi, Anda hanya perlu mengisi formulir dan selesai.
Mari kita beri contoh, kita akan mengubah bilangan z = √85 12,53 ke dalam bentuk trigonometri.
Kedua variabel (modul dan argumen) kita rumuskan kembali ke dalam persamaan bentuk trigonometri:
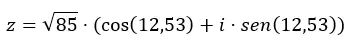
Jadi, sekarang setelah Anda mengetahui cara bertransisi dari satu bentuk ke bentuk lainnya, kami sarankan untuk berlatih sedikit dengan beberapa latihan . Dengan cara ini Anda akan mengkonsolidasikan pengetahuan yang dipelajari dalam artikel ini. Jika Anda memiliki pertanyaan mengenai topik ini, silakan tinggalkan di komentar. Dan jika Anda ingin mempelajari lebih lanjut tentang bilangan kompleks, lihat tautan di bawah.