Sejak zaman kuno, himpunan bilangan asli telah menjadi fondasi banyak cabang matematika dibangun. Misalnya, aritmatika dan geometri didasarkan pada angka-angka ini. Oleh karena itu, pada artikel singkat kali ini kita akan melihat pengertian bilangan asli dan segala konsep yang berhubungan dengan himpunan tersebut.
Berapakah bilangan asli?
Bilangan asli adalah sekumpulan elemen abstrak yang kita gunakan untuk menghitung dan mengurutkan objek di dunia fisik. Dalam matematika, himpunan bilangan asli umumnya dilambangkan dengan huruf ℕ. Ini terdiri dari semua bilangan bulat positif tanpa desimal dan bukan pecahan: ℕ = {1, 2, 3, 4, 5, 6…}.
Dengan kata lain, bilangan asli adalah bilangan bulat positif yang dapat digunakan untuk menghitung benda nyata. Dengan demikian kita dapat mengatakan bahwa bilangan 1 adalah bilangan asli karena kita dapat menggunakannya untuk menghitung benda nyata. Misalnya, kita dapat memiliki sebuah apel dan dua buah pir, sehingga totalnya menjadi 3 buah.
Pada gambar berikut, kami akan menampilkan diagram yang merangkum semua himpunan bilangan, sehingga Anda dapat melihat di mana letak himpunan tersebut. Dan hubungan apa yang dimilikinya dengan yang lain, untuk lebih mengasimilasi gagasan bilangan asli. Sebaiknya, sebelum melanjutkan penjelasan, Anda mencermati peta konsep dengan baik dan mencoba memahaminya.

Bagaimana cara mengetahui suatu bilangan natural atau bukan?
Seperti yang telah kami katakan, bilangan asli adalah bilangan yang kita gunakan untuk menghitung dan mengurutkan. Untuk mengetahui suatu nilai natural atau tidak, kita harus memperhatikan hal-hal berikut : bilangan ℕ tidak mempunyai tanda negatif, tidak mempunyai tempat desimal, tidak mempunyai satuan imajiner dan bukan pecahan. Selanjutnya, kami tunjukkan daftar 100 bilangan asli pertama:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 6 4, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75 , 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 dan 100 .
Bagaimana bilangan asli dibaca dan ditulis?
Bilangan asli mengikuti sistem bilangan desimal , artinya nilainya mempunyai bilangan sepuluh sebagai basis aritmatikanya. Semua bilangan terdiri dari setidaknya satu dari sembilan digit berikut: 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Dan ingat, bilangan asli tidak pernah memiliki koma desimal atau tanda negatif .
Sejauh menyangkut semua operasi aritmatika, angka-angka ini ditulis mengikuti notasi matematika . Jika Anda memiliki keraguan tentang suatu simbol atau ekspresi , kami menyarankan Anda mengakses tautan terakhir ini dan membaca artikelnya. Di sana Anda akan menemukan semua informasi yang berkaitan dengan bahasa matematika dan semua notasinya.
Ciri-ciri bilangan asli
Beberapa ciri terpenting bilangan asli adalah:
- Bilangan asli pertama adalah 1, karena 0 bukanlah bilangan asli.
- Mereka digunakan untuk mengukur, mengontrol dan menghitung: mereka dapat digunakan untuk mengukur panjang, berat, kapasitas, dll.
- Mereka dapat dibandingkan satu sama lain: kita dapat menentukan mana yang lebih besar atau lebih kecil dari bilangan asli lainnya.
- Mereka memiliki urutan: bilangan asli mengikuti urutan logis, dimulai dengan 1 dan berakhir di tak terhingga.
- Dua sifat alami tidak dapat memiliki penerus yang sama, atau pendahulu yang sama.
- Semua bilangan asli adalah bilangan bulat, karena bilangan asli adalah bilangan bulat positif, bukan desimal atau pecahan.
Sebagai penutup bagian ini, kami tinggalkan serangkaian klarifikasi tentang himpunan ini yang sering menimbulkan keraguan di kalangan siswa: bilangan nol bukanlah bilangan asli, bilangan asli adalah bilangan bulat, bilangan asli tidak boleh bilangan negatif , bilangan asli tidak memiliki desimal tempat, dan bilangan asli tidak terhingga.
Representasi bilangan asli
Himpunan bilangan asli disebut juga ℕ, dibentuk oleh bilangan bulat positif: 1, 2, 3, 4… dan seterusnya. Himpunan ini diwakili oleh notasi berikut: ℕ = {1, 2, 3, 4, 5…}. Namun, angka-angka tersebut juga dapat direpresentasikan secara lebih grafis, dengan menempatkannya pada garis bilangan .
Cara kedua ini dilakukan dengan menggambar garis lurus mendatar dan menuliskan nilai bilangan asli secara teratur di sepanjang garis tersebut. Agar Anda dapat dengan mudah memvisualisasikan urutan himpunan , sistem ini sangat baik bagi mereka yang mempelajari himpunan numerik ini. Pada gambar berikut Anda dapat melihat seperti apa tata letak barisnya.
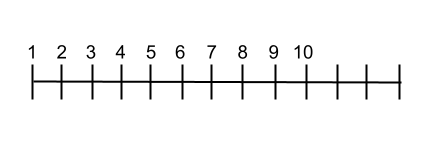
Operasi dengan bilangan asli
Sekarang setelah Anda mengetahui semua karakteristik dan properti himpunan ℕ, sekarang saatnya menerapkannya pada operasi aritmatika , yang merupakan penerapan utama bilangan-bilangan ini. Selanjutnya akan dijelaskan secara detail keempat operasi dasar (penjumlahan, pengurangan, perkalian dan pembagian).
Saat kita menjumlahkan nilai natural, kita mendapatkan bilangan lain ℕ: 3 + 6 = 9 . Namun jika kita mengurangkan bilangan asli, hasilnya bisa berupa bilangan positif atau negatif. Yang terakhir ini tidak termasuk dalam himpunan yang sedang kita bicarakan, jadi hanya pengurangan yang mempunyai hasil positif yang merupakan bagian dari himpunan ℕ: 4 – 2 = 2 .
Perkalian bilangan asli sama dengan perkalian bilangan asli, karena hanya dapat menghasilkan bilangan positif. Misalnya, jika kita ingin mengalikan 3 dan 8, hasilnya adalah 3 · 8 = 24 . Namun, jika kita membagi angka-angka dalam himpunan ℕ, dalam kasus tertentu kita dapat memperoleh angka desimal . Dalam situasi ini, hasil bukanlah bagian dari keseluruhan yang alami.
Oleh karena itu, dalam himpunan bilangan asli, hanya penjumlahan dan perkalian yang didefinisikan. Kedua operasi ini memeriksa sifat komutatif dan asosiatif . Oleh karena itu, jika bilangan awalnya asli, maka hasilnya selalu bilangan asli. Dengan cara ini, ini adalah operasi yang selalu menghormati properti himpunan ℕ.
Penerapan bilangan asli
Bilangan asli sering digunakan dalam kehidupan sehari-hari . Misalnya, mereka dapat digunakan untuk mengukur panjang meja atau waktu yang dibutuhkan seseorang untuk berjalan ke toko. Mereka juga dapat digunakan untuk melakukan perhitungan matematis, seperti penjumlahan atau pengurangan. Bilangan bulat juga dapat digunakan untuk menentukan posisi benda dalam suatu ruang, seperti meletakkan buku di rak.