Bilangan kompleks adalah himpunan yang terdiri dari bilangan real dan bilangan imajiner . Dua himpunan numerik terakhir ini dapat direpresentasikan secara grafis menggunakan garis nyata dan garis imajiner. Dan ketika kita menempatkan kedua garis pada bidang yang sama, bidang kompleks yang terkenal akan terbentuk.
Apa rencana rumitnya?
Bidang kompleks dibentuk oleh sumbu nyata (sumbu X), yang ekuivalen dengan garis nyata, dan sebaliknya, sumbu imajiner (sumbu Y), yang mengkonsep garis imajiner.
Perlu dicatat bahwa rencana ini mencakup semua bilangan kompleks. Oleh karena itu, tidak peduli seberapa kecil atau kecilnya, atau dalam bentuk apa bilangan kompleks dituliskan, bilangan tersebut dapat direpresentasikan secara grafis pada denah. Jadi mari kita lihat bagaimana angka-angka ini direpresentasikan dalam bidang kompleks.
Bagaimana cara membuat grafik bilangan kompleks pada bidang kompleks?
Seperti yang telah kita ketahui (atau jika Anda belum mengetahuinya, kami sarankan Anda membaca artikel kami tentang bilangan kompleks ), ada tiga cara untuk menulis bilangan kompleks: bentuk binomial, bentuk polar, dan bentuk trigonometri. Masing-masing menyatakan nilai kompleks menurut struktur yang berbeda, sehingga metode yang diikuti untuk membuat representasi grafis berbeda.
Selanjutnya, kami menjelaskan prosedur yang harus diikuti dalam tiga kasus:
Representasi dalam bentuk binomial
Jika kita memiliki bilangan kompleks dalam notasi binomial , yang merupakan notasi paling umum, kita harus melihat struktur bilangan tersebut:

dimana a adalah bagian nyata dan b adalah bagian imajiner.
Mengetahui hal tersebut, kita menyimpulkan bahwa nilai a adalah nilai yang kita gunakan untuk absis (sumbu nyata) dan nilai b adalah nilai yang kita gunakan untuk komputer (sumbu imajiner). Dengan contoh berikut Anda akan memahaminya dengan lebih baik.
Kita akan mencoba merepresentasikan bilangan: 3 + 2i.
Hal pertama yang dilakukan adalah menggambar grafiknya (perhatikan bahwa sumbu horizontal adalah sumbu nyata dan sumbu vertikal adalah sumbu imajiner):

Kemudian, kita cari titik grafiknya dalam koordinat Cartesian (x, y), yang kita simpulkan dari bilangan kompleksnya. Dalam contoh praktis ini, maksud kita adalah (3, 2).
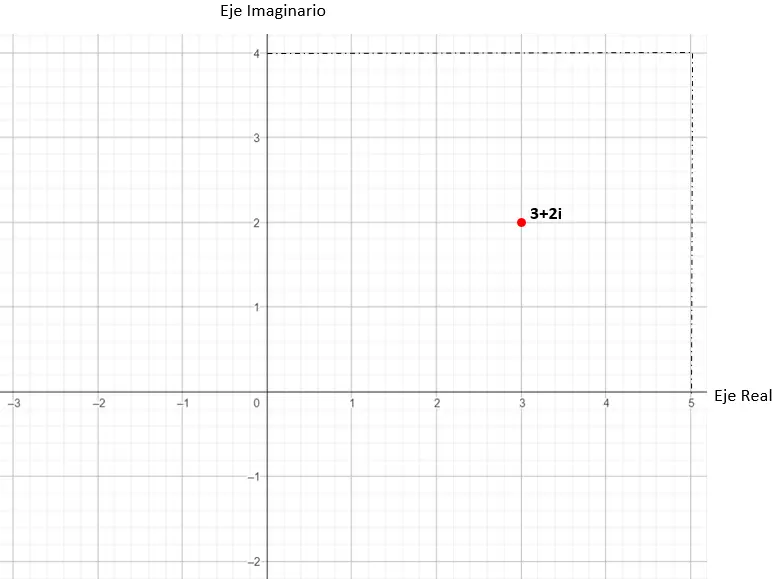
Jadi nilai 3 + 2i akan direpresentasikan dalam bidang kompleks.
Representasi dalam bentuk kutub
Sekarang kita akan melihat bagaimana bilangan kompleks direpresentasikan dalam bentuk polar . Untuk memahami metode ini sepenuhnya, Anda perlu mengetahui bahwa notasi polar mendefinisikan bilangan kompleks berdasarkan modul dan argumennya. Yang digunakan dalam representasi grafis sebagai koordinat kutub (dan bukan sebagai koordinat Cartesian!).
Dan ciri utama sistem koordinat kutub adalah letak suatu titik digambarkan melalui vektor dan sudut (tidak seperti cara sebelumnya). Yang sesuai dengan modul dan argumen bilangan kompleks. Selanjutnya, kami tunjukkan rumus universal bentuk polar bilangan kompleks:

Dimana |z| adalah modulusnya dan α adalah argumennya. Kedua variabel ini diterjemahkan dalam rencana dengan:
- Modul: itu adalah panjang yang mendefinisikan sebuah vektor (antara titik asal dan titik yang setara dengan bilangan kita).
- Argumen: adalah sudut yang dibentuk vektor terhadap sumbu X.
Oleh karena itu, modulus bilangan kompleks sesuai dengan panjang vektor yang kita gunakan untuk membuat grafik. Sedangkan argumen atau sudut bilangan kompleks adalah sudut antara vektor dan sumbu X. Di bawah ini Anda dapat melihat diagram yang menempatkan semua variabel :
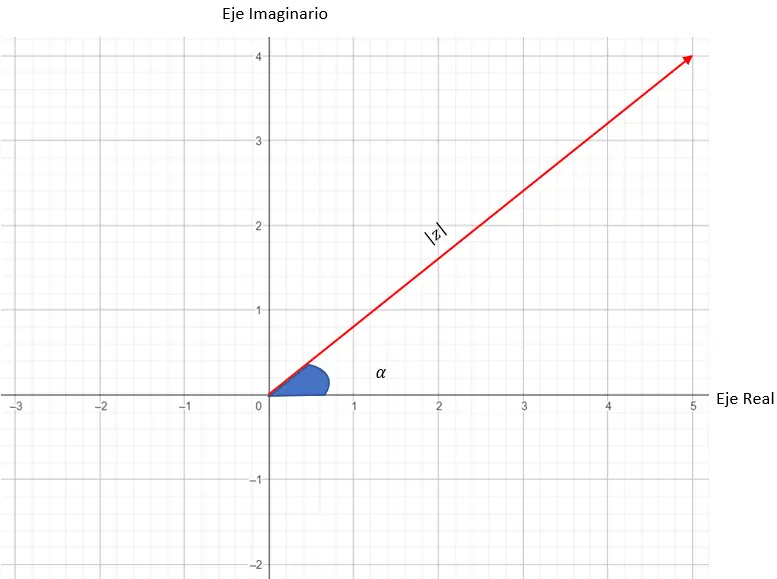
Sekarang kita akan mencoba merepresentasikan bilangan tersebut: 3 45 .
Pertama, kita perlu mengidentifikasi modul dan argumennya:
- Modul: 3.
- Argumen: 45 derajat.
Selanjutnya kita perlu mencari titik-titik pada grafik yang memiliki modulus sama dengan 3, dalam hal ini titik mana pun pada lingkaran berjari-jari 3 dapat digunakan.
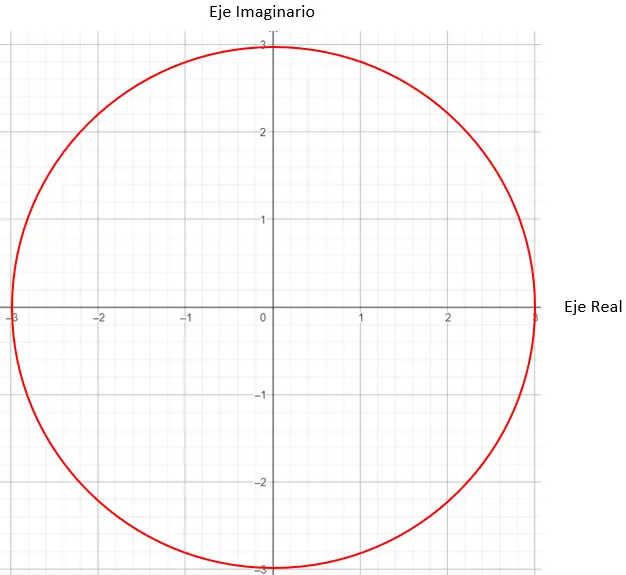
Dan untuk menyelesaikan penentuan titik pastinya, kita harus memberikan syarat bahwa vektor yang dihasilkan modul dan titik asal harus membentuk sudut 45 derajat dengan sumbu X.
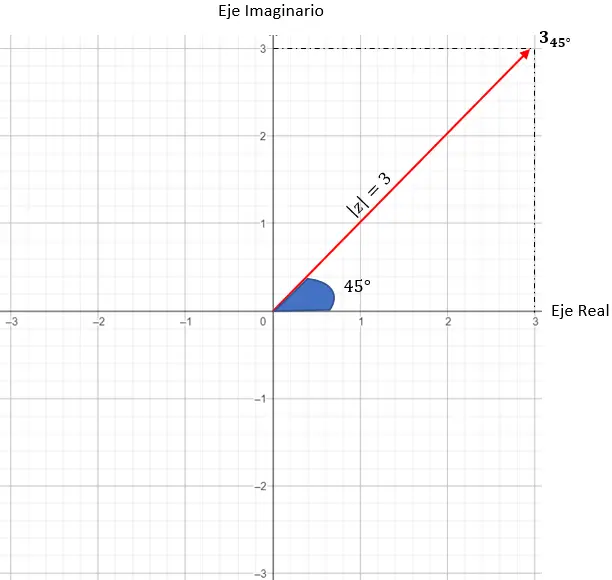
Dan kita sudah memiliki bilangan kompleks yang direpresentasikan dalam notasi kutub.
Representasi dalam bentuk trigonometri
Terakhir, kita masih harus menjelaskan bagaimana bilangan kompleks direpresentasikan dalam bentuk trigonometri . Kasus ini dan kasus sebelumnya pada dasarnya sama, karena bentuk polar dan bentuk trigonometri menggunakan data yang sama untuk menyatakan bilangan kompleks: modulus dan argumen. Ini hanya mengubah struktur ekspresi:

Dimana, |z| adalah modulusnya dan α adalah argumennya.
Oleh karena itu kita harus memanfaatkan metode yang sama seperti pada kasus sebelumnya: gunakan modul sebagai “panjang” dan argumen sebagai sudut. Dengan melihat contoh berikut ini, Anda akan lebih memahaminya.
Kita akan menyatakan z = 4 · (cos (45) + i · sin(45)).
Hal pertama adalah mengidentifikasi modul dan sudutnya:
- Modul: 4.
- Argumen: 45 derajat.
Selanjutnya kita perlu mencari titik-titik pada grafik yang memiliki modulus sama dengan 4, dalam hal ini titik mana pun pada lingkaran berjari-jari 4 dapat digunakan.
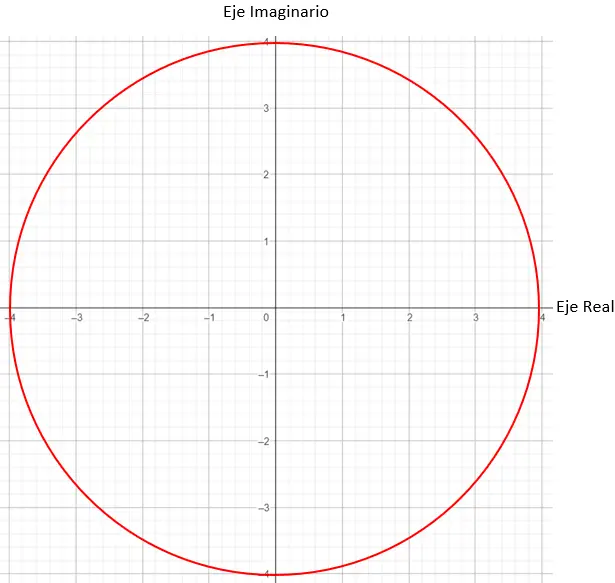
Dan terakhir, kita menemukan titik tepatnya, yang mengharuskan sudut yang terbentuk antara vektor modulus dan sumbu X adalah 45 derajat, seperti yang dijelaskan dalam argumen tersebut.
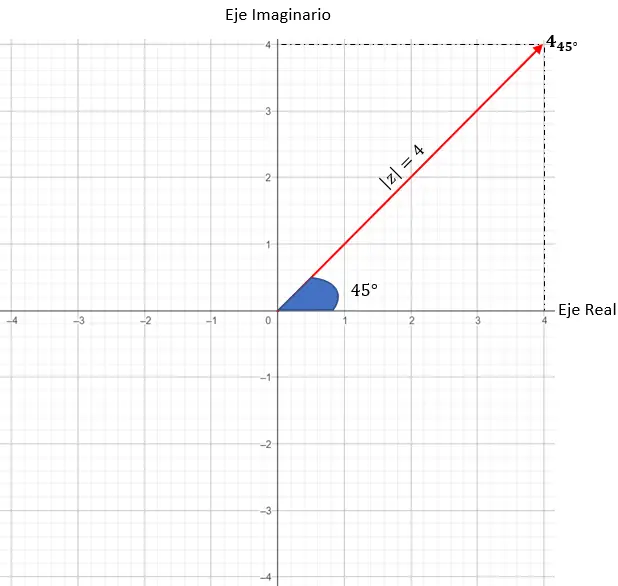
Jadi kami merepresentasikan bilangan kompleks dalam bentuk trigonometri.
Latihan pesawat yang kompleks
Untuk mengakhiri publikasi ini, kami akan menawarkan satu latihan terakhir. Kami sangat menyarankan Anda menyelesaikannya, karena dengan cara ini Anda akan mengkonsolidasikan pengetahuan yang dijelaskan di seluruh artikel ini.
Bukti representasi grafis dari tiga bilangan kompleks berikut pada bidang kompleks:
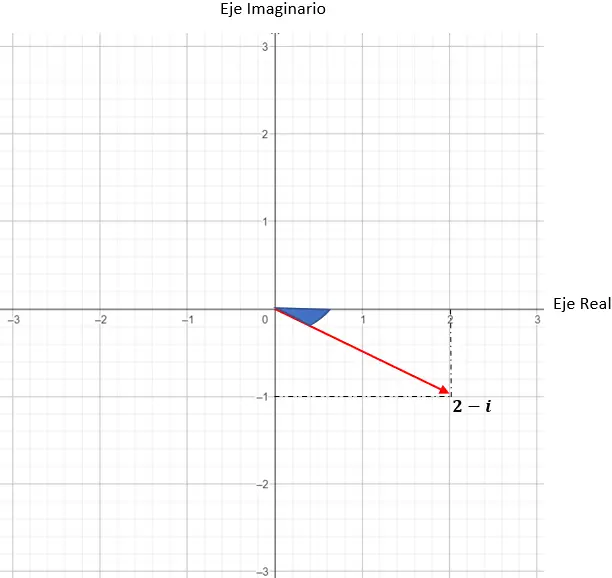
z = 2 – saya
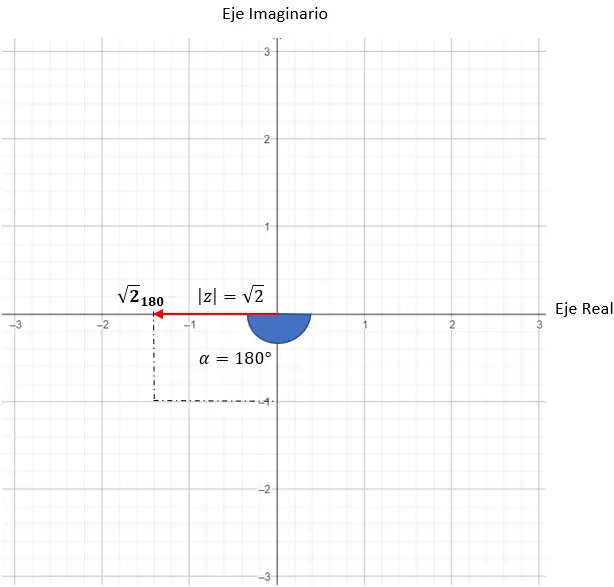
w = √2180
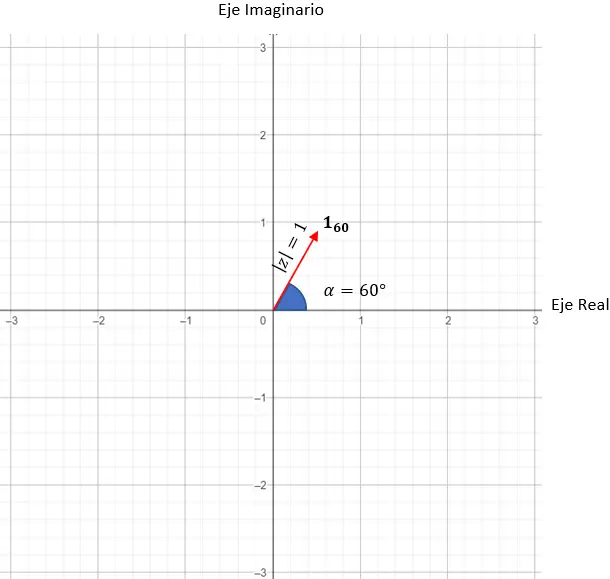
p = cos(60) + saya dosa(60)