Di sini Anda akan menemukan cara menurunkan fungsi kosinus (rumus). Anda akan dapat melihat contoh turunan fungsi kosinus dan berlatih dengan latihan langkah demi langkah. Selain itu, kami tunjukkan bukti rumusnya, berapakah turunan kedua dari cosinus dan bahkan turunan dari invers cosinus.
Berapakah turunan dari cosinus?
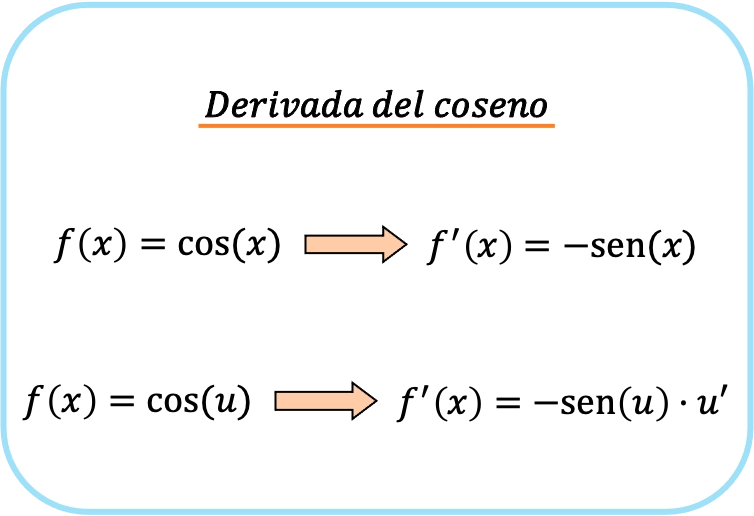
Turunan fungsi kosinus adalah fungsi sinus termodifikasi tanda. Dengan kata lain, turunan cosinus x sama dengan dikurangi sinus x.
Jika terdapat suatu fungsi dalam argumen kosinus, maka turunan kosinusnya adalah hasil kali dikurangi sinus fungsi tersebut dikalikan dengan turunan fungsi tersebut.
Rumus kedua setara dengan rumus pertama namun menerapkan aturan rantai. Jadi, secara ringkas rumus turunan cosinusnya adalah sebagai berikut:
Contoh turunan kosinus
Setelah kita mengetahui apa itu rumus kosinus, kami akan menjelaskan beberapa contoh turunan trigonometri jenis ini agar Anda tidak ragu lagi bagaimana cara menurunkan fungsi kosinus.
Contoh 1: Turunan dari kosinus 2x
Dalam argumen kosinus kita tidak memiliki satu x pun, melainkan fungsi yang lebih kompleks. Oleh karena itu, kita perlu menggunakan rumus berikut untuk menurunkan kosinus:
Karena turunan 2x adalah 2, maka turunan cosinus 2x dikurangi sinus 2x dikalikan 2.
Contoh 2: Turunan dari kosinus x kuadrat
Seperti pada contoh sebelumnya, dalam argumen cosinus kita mempunyai fungsi yang berbeda dari x, jadi kita akan menggunakan aturan rantai untuk menurunkan kosinus:
Maka turunan dari x 2 adalah 2x, maka turunan cosinus x yang dipangkatkan 2 adalah:
Contoh 3: Turunan dari kosinus pangkat tiga
Fungsi kosinus dalam contoh ini terdiri dari fungsi lain, jadi kita perlu menerapkan rumus berikut untuk menyelesaikan turunannya:
Jadi, dengan menerapkan rumus tersebut, kita mendapatkan turunan dari fungsi tersebut:
![\begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73284bcfb1d5647b2304e323e7fbaedf_l3.png "Rendered by QuickLaTeX.com")
➤ Untuk membedakan fungsi ini, Anda juga harus menggunakan rumus turunan fungsi potensial .
Turunan kedua dari kosinus
Selanjutnya kita akan melihat bahwa turunan kedua sinus dapat dengan mudah dihitung berkat karakteristik fungsi trigonometri.
➤ Catatan: Untuk memahami hal berikut ini, Anda perlu mengetahui apa itu turunan sinus .
Turunan kedua kosinus x dikurangi kosinus x. Ini mungkin tampak aneh, tapi secara matematis memang seperti itu. Memang, turunan dari sinus adalah kosinus dan, oleh karena itu, dengan mendiferensiasikan kosinus x dua kali, kosinus diperoleh kembali tetapi dengan tanda yang dimodifikasi.
![\begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0d9dda8a4031c367120b1f950da4391_l3.png "Rendered by QuickLaTeX.com")
Properti ini berubah jika argumen kosinusnya bukan x, karena dalam kasus ini kita menyeret suku aturan rantai:
![\begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83d86bd6508f06b0723153b3b9254c1f_l3.png "Rendered by QuickLaTeX.com")
Turunan dari kosinus terbalik
Semua fungsi trigonometri mempunyai fungsi invers sehingga fungsi kosinus juga dapat diinvers. Demikian pula, kosinus terbalik dapat terdiferensiasi.
Turunan invers cosinus suatu fungsi adalah dikurangi turunan fungsi tersebut dibagi akar kuadrat satu dikurangi kuadrat fungsi tersebut.
Ingatlah bahwa kosinus terbalik juga disebut arccosine.
Misalnya turunan dari invers cosinus 3x adalah:
Latihan soal turunan kosinus
Hitung turunan fungsi kosinus berikut:
![\begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f4645fb77435daec6f696cffbd54884_l3.png "Rendered by QuickLaTeX.com")
Bukti turunan kosinus
Terakhir, kita akan mendemonstrasikan secara matematis rumus turunan kosinus x. Untuk melakukan ini, kita akan menggunakan definisi turunan, yang sesuai dengan limit berikut:
Kita akan buktikan cosinusnya, jadi fungsinya adalah cos(x):
Kita tidak dapat menyelesaikan batasan ini dengan substitusi, karena kita akan berakhir pada ketidakpastian. Namun, kita dapat menyatakan kosinus suatu jumlah dengan cara lain dengan menerapkan identitas trigonometri berikut:
Langkah selanjutnya adalah memisahkan pecahan menjadi dua pecahan dan mengambil faktor persekutuan kosinusnya:
![\displaystyle f'(x)=\lim_{h \to 0}\left[\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\frac{\text{sen}(x)\text{sen}(h)}{h}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-c7c1cd89cf290b01d7d72fc8084f6529_l3.png "Rendered by QuickLaTeX.com")
Limit suatu pengurangan sama dengan pengurangan limitnya, maka:
Kosinus dari x dan sinus dari x tidak bergantung pada h, sehingga kita dapat mengeluarkannya ke luar batas:
Dengan menggunakan perhitungan limit dengan ekuivalen yang sangat kecil, kita menyimpulkan bahwa limit pertama adalah 0 dan limit kedua adalah 1. Oleh karena itu:
Dan kita sudah sampai pada rumus turunan fungsi kosinus, sehingga persamaannya terbukti.