Di sini Anda akan mengetahui cara menyelesaikan batas trigonometri. Anda akan dapat melihat beberapa contoh limit fungsi trigonometri dan bahkan berlatih dengan latihan langkah demi langkah tentang limit trigonometri.
Apa yang dimaksud dengan limit trigonometri?
Batas trigonometri adalah batas yang dihitung pada fungsi trigonometri. Untuk menyelesaikan limit trigonometri harus dilakukan prosedur pendahuluan, karena umumnya menimbulkan ketidakpastian.
Selain itu, limit fungsi trigonometri tak hingga tidak ada karena merupakan fungsi periodik. Artinya, grafiknya terus berulang secara berkala tanpa cenderung ke arah nilai tertentu.
Rumus Batas Trigonometri
Semua batas trigonometri dihitung dari dua rumus berikut:
![]()
Jika kita mencoba menghitung limit dengan substitusi, kita memperoleh ketidakpastian nol antara nol:
![]()
Namun rumus trigonometri ini dapat dibuktikan dengan menghitung nilai fungsi yang lebih dekat dan lebih dekat ke x=0 (sudut dalam radian).
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(-1)=\cfrac{\text{sen}(-1)}{-1}=0,84147\\[3ex]f(-0,1)=\cfrac{\text{sen}(-0,1)}{-0,1}=0,99833\\[3ex]f(-0,01)=\cfrac{\text{sen}(-0,01)}{-0,01}=0,99998\\[3ex]f(-0,001)=\cfrac{\text{sen}(-0,001)}{-0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ccd668acef73b9140a0cbbb9c1d53ad3_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(1)=\cfrac{\text{sen}(1)}{1}=0,84147\\[3ex]f(0,1)=\cfrac{\text{sen}(0,1)}{0,1}=0,99833\\[3ex]f(0,01)=\cfrac{\text{sen}(0,01)}{0,01}=0,99998\\[3ex]f(0,001)=\cfrac{\text{sen}(0,001)}{0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-66152efc3ce1fa761186a65db677af27_l3.png)
Dua limit lateral fungsi trigonometri menghasilkan 1, jadi limit di titik x=0 adalah 1:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\\[3ex]\color{orange}\bm{\downarrow}\\[2ex]\lim_{x\to 0}\displaystyle\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8af649189957b154866097e315f7cb92_l3.png)
Jadi, limit trigonometri sinus x dibagi x karena x cenderung 0 sama dengan 1.
Rumus ini juga bisa diterapkan untuk beberapa sudut:
![]()
![]()
Jika kita mencoba mencari limit dengan substitusi langsung, kita memperoleh bentuk tak tentu nol antara nol:
![]()
Tapi kita bisa memeriksa kesetaraannya dari rumus di atas. Untuk melakukannya, pertama-tama Anda harus mengalikan pembilang dan penyebut pecahan dengan 1 ditambah kosinus x:
![]()
Kita sekarang mempunyai identitas penting pada pembilang pecahan, sehingga kita dapat menyederhanakannya:
![]()
![]()
Berdasarkan identitas trigonometri dasar, kita menulis ulang pembilangnya:
![]()
![]()
Oleh karena itu, kita dapat mengubah pecahan menjadi hasil kali pecahan:
![]()
![]()
Dengan menggunakan sifat-sifat limit, kita dapat mengubah persamaan di atas menjadi hasil kali limit:
![]()
Dengan menggunakan rumus di atas, kita dapat dengan mudah menyederhanakan limit trigonometri:
![]()
![]()
![]()
Dan terakhir, kami menghitung batas yang dihasilkan:
![]()
Oleh karena itu, rumus limit trigonometri diverifikasi:
![]()
Seperti rumus lainnya, rumus ini juga dapat digunakan untuk berbagai sudut:
![]()
Oleh karena itu, untuk menyelesaikan limit trigonometri, kita harus menggunakan aritmatika untuk mengubah fungsi dan memperoleh ekspresi yang serupa dengan ini. Dengan cara ini kita dapat menggunakan salah satu dari dua rumus tersebut dan mencari nilai limitnya.
Di sisi lain, terkadang kami mungkin perlu menerapkan identitas trigonometri tertentu, jadi kami serahkan semua rumus di bawah ini kepada Anda
Rumus yang menghubungkan tiga perbandingan trigonometri utama:
![]()
Identitas trigonometri dasar:
![]()
Hubungan trigonometri diturunkan dari dasar:
![]()
![]()
Sudut yang berhadapan:
![]()
![]()
![]()
Jumlah dua sudut:
![]()
![]()
![]()
Perbedaan dua sudut:
![]()
![]()
![]()
Sudut ganda:
![]()
![]()
![]()
Setengah sudut:
![]()
![]()
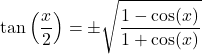
Penjumlahan dan pengurangan sinus dan cosinus:
![]()
![]()
![]()
![]()
Hasil kali sinus dan cosinus:
![]()
![]()
![]()
Agar Anda dapat melihat dengan tepat cara menghitung batas trigonometri, kami telah mengumpulkan contoh langkah demi langkah di bawah ini.
Contoh limit trigonometri
Mari kita lihat bagaimana penyelesaian limit trigonometri menggunakan contoh berikut:
![]()
Mencoba menghitung limit trigonometri, kita memperoleh ketidakpastian nol antara nol:
![]()
➤ Lihat: batas nol antara nol
Oleh karena itu, perlu dilakukan transformasi fungsi trigonometri untuk menyelesaikan limitnya. Fungsi tangen sama dengan sinus dibagi kosinus, jadi:
![]()
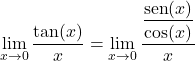
Sekarang kita dapat menyatakan fungsi tersebut sebagai hasil kali dengan menerapkan sifat-sifat pecahan:
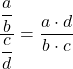
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{\displaystyle\frac{x}{1}}=\lim_{x\to 0}{\frac{\text{sen}(x)\cdot 1}{\text{cos}(x) \cdot x}=\\[6ex]\displaystyle =\lim_{x\to 0}{\frac{\text{sen}(x)}{x\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{1}{\text{cos}(x)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dd10c321c3b7dc40698b318c7187a3c4_l3.png)
Dengan menggunakan sifat-sifat limit, kita dapat mengubah limit dua fungsi yang dikalikan menjadi hasil kali dua limit:
![]()
Seperti yang kami tunjukkan di atas, limit trigonometri pertama menghasilkan 1:
![]()
![]()
Jadi lakukan saja perhitungan berikut:
![]()
Latihan soal batas trigonometri diselesaikan
Latihan 1
Selesaikan limit trigonometri berikut:
![]()
Pertama, kita coba menghitung limit trigonometri dengan evaluasi langsung:
![]()
Tapi kita mendapatkan ketidakpastian yang nol di atas nol. Jadi kita perlu menerapkan transformasi pada fungsinya.
Pertama, kita biarkan saja x pada penyebutnya dengan melakukan hal berikut:
![]()
Sekarang kita mengalikan dan membagi pecahan dengan 4 untuk mendapatkan ekspresi yang dapat diterapkan rumus limit trigonometri pertama:
![]()
Terakhir, kami menerapkan rumus yang terlihat di awal dan menyelesaikan limit trigonometri:
![]()
![]()
Latihan 2
Hitung limit trigonometri berikut:
![]()
Pertama, kita coba mencari limit trigonometri:
![]()
Tetapi bentuk tak tentu nol yang bersesuaian dengan nol tercapai.
Kemudian, kita ubah tangen menjadi hasil bagi sinus dan kosinus:
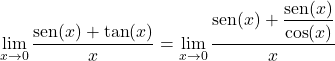
Kita kalikan dan bagi dengan kosinus x:
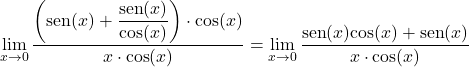
Kita ambil faktor persekutuan dalam pembilangnya dan kita pisahkan limit trigonometrinya menjadi dua:
![]()
Dan terakhir, kita temukan hasil limit trigonometri:
![]()
Latihan 3
Selesaikan limit fungsi trigonometri berikut ketika x mendekati nol:
![]()
Dengan melakukan perhitungan langsung diperoleh batas tak tentu 0 antara 0:
![]()
Jadi, kita akan menyederhanakan limitnya dengan membagi setiap suku dengan tangen x:
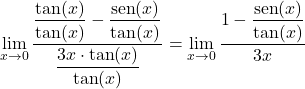
Kedua, kita dapat menyimpulkan dari identitas trigonometri dasar bahwa pecahan pembilangnya setara dengan kosinus x:
![]()
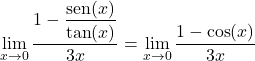
Dan dengan menerapkan rumus kedua yang ditunjukkan dalam teori limit trigonometri, kita dapat dengan mudah menyelesaikan limitnya:
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}=\lim_{x\to 0}\frac{1}{3}\cdot \frac{1-\text{cos}(x)}{x}=\\[4ex]\displaystyle =\frac{1}{3}\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=\frac{1}{3}\cdot 0=\bm{0}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1ee20bc86ad7559fcda3d6bad3c9b27_l3.png)
Latihan 4
Tentukan penyelesaian limit trigonometri berikut di titik x=0:
![]()
Jika kita mencoba menyelesaikan limitnya, kita mendapatkan bentuk tak tentu 0/0:
![]()
Ekspresi aljabar untuk pembilangnya dapat ditulis ulang menggunakan identitas trigonometri sinus sudut ganda:
![]()
![]()
Sekarang mari kita pisahkan limit fungsi trigonometri menjadi suatu hasil kali:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)\cdot \text{sen}(5x)}{x\cdot x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc650634075435b782f1e7b921b77c02_l3.png)
Dan terakhir, kita menyelesaikan limit trigonometri dengan menerapkan sifat-sifat limit:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =2\cdot \lim_{x\to 0}\frac{\text{sen}(2x)}{2x}\cdot 5\cdot \lim_{x\to 0}\frac{\text{sen}(5x)}{5x}=\\[4ex]\displaystyle =2\cdot 1\cdot 5\cdot 1=\bm{10}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c26ba3032828541e69e4bd976ac4f96_l3.png)