Batas samping

Pada artikel ini kami akan menjelaskan apa itu limit lateral suatu fungsi (beserta contoh). Kami juga mengajari Anda cara menghitung batas lateral kiri dan kanan suatu fungsi, baik secara grafis maupun numerik. Selain itu, Anda akan dapat berlatih dengan latihan yang diselesaikan selangkah demi selangkah dari batas lateral.

Berapakah batas lateralnya?

Batas lateral suatu fungsi pada suatu titik mempelajari perilaku fungsi tersebut di sekitar titik tersebut. Terdapat limit lateral kiri dan limit lateral kanan, yang menganalisis nilai fungsi di kiri dan kanan titik yang ditinjau.

Batas lateral kiri dan kanan

Seperti yang kita lihat pada definisi batas lateral, ada dua jenis: batas lateral kiri dan batas lateral kanan.

Limit kiri suatu fungsi dinyatakan dengan tanda minus pada titik dimana limit tersebut dianalisis, dan sebaliknya limit kanan dinyatakan dengan tanda plus.

Perhatikan contoh berikut untuk lebih memahami pengertian batas lateral:

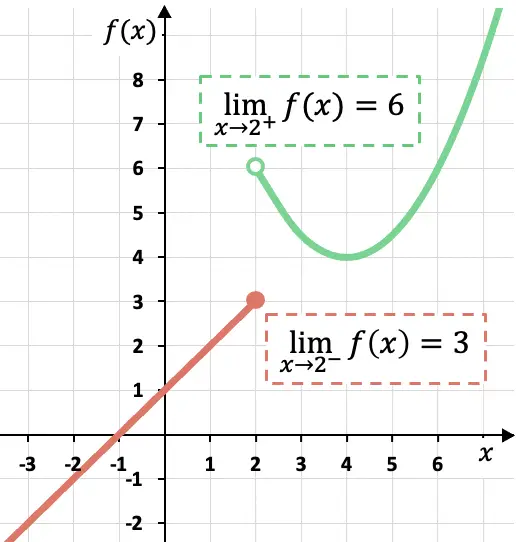
Seperti yang dapat Anda lihat dalam representasi grafis dari fungsi sepotong-sepotong ini, batas lateral bergantung pada sisi penghitungannya.

Dalam hal ini, fungsi tersebut mendekati 3 ketika x mendekati 2 dari kiri, karena fungsi tersebut mengambil nilai mendekati 3 ketika x mendekati x=2 dari kirinya.

Sebaliknya, batas lateral fungsi di x=2 oleh garis bernilai 6. Karena jika kita mendekati titik x=2 melalui garisnya, maka fungsi tersebut mengambil nilai semakin mendekati f(x)= 6.

Sebaliknya perlu anda ketahui bahwa batas lateral mempunyai sifat yang sama dengan batas biasa. Di tautan berikut Anda dapat melihat apa saja properti batasnya:

➤ Lihat: properti batas

batas lateral yang sama

Kita baru saja melihat contoh batas sisi suatu fungsi berbeda, tapi… apa yang terjadi jika batas sisinya sama?

Jika kedua batas lateral suatu fungsi di suatu titik ada dan sama , maka limit fungsi tersebut ada di titik tersebut dan hasil limitnya adalah nilai batas lateralnya.

Dengan kata lain, agar limit suatu fungsi ada di suatu titik, syarat berikut harus dipenuhi:

Oleh karena itu, jika batas lateral suatu fungsi di suatu titik berbeda, maka batas fungsi di titik tersebut tidak ada.

Selain itu, keberadaan limit suatu fungsi di suatu titik merupakan syarat penting agar fungsi tersebut kontinu di suatu titik .

Mari kita selesaikan sebuah contoh untuk menyelesaikan pemahaman konsep batas lateral:

Batas lateral pada titik x=-2 dari fungsi yang direpresentasikan secara grafis sama, karena nilai fungsi cenderung ke arah 3 baik kita mendekati x=-2 dari kiri atau dari kanan. Oleh karena itu, limit fungsi di x=-2 sama dengan 3.

Sebaliknya, pada titik x=4 batas lateralnya berbeda, karena dari kiri fungsinya mendekati f(x)=3 tetapi dari kanan fungsinya mendekati f(x)=2. Oleh karena itu, limit fungsi pada titik ini tidak ada.

Perhitungan batas lateral

Dengan mengetahui definisi batas lateral, kita akan melihat cara menghitungnya secara numerik dengan menyelesaikan contoh berikut:

Jika kita menghitung limit seperti biasa, kita memperoleh ketidakpastian suatu bilangan real dibagi 0:

Namun, saat menghitung batas lateral, kami tidak mendapatkan ketidakpastian apa pun.

Untuk menghitung limit lateral fungsi dari kiri pada x=2, Anda harus mengambil bilangan yang lebih kecil dari x=2 tetapi sangat dekat dengannya, misalnya x=1,999.

Dalam hal ini penyebutnya adalah bilangan negatif dengan nilai yang sangat kecil tetapi tidak genap nol, dan biasanya diwakili oleh tanda nol dan tanda minus di depannya:

Oleh karena itu, hasil batas lateralnya adalah dikurangi tak terhingga, karena bilangan apa pun yang dibagi 0 menghasilkan tak terhingga, dan bilangan positif dibagi negatif menghasilkan negatif:

Kita dapat memverifikasi bahwa fungsi tersebut mendekati minus tak terhingga dengan menghitung gambar fungsi yang nilainya mendekati x=2 dari kiri.

Demikian pula, untuk mencari limit fungsi di titik x=2 di sebelah kanan, kita dapat menerapkan alasan yang sama: kita mengambil nilai yang lebih besar dari 2 tetapi sangat dekat, seperti tahun 2001.

Dengan cara yang sama, kita dapat memverifikasi bahwa suatu fungsi cenderung tak terhingga dengan menghitung bayangan fungsi yang nilainya semakin mendekati x=2 dari kanan.

Pada grafik berikut Anda dapat melihat representasi fungsi yang dianalisis. Seperti yang Anda lihat, limit lateral fungsi di titik x=2 di sebelah kiri adalah minus tak terhingga, dan limit lateral fungsi di titik x=2 di sebelah kanan adalah plus tak terhingga.

Masalah batas lateral diperbaiki

Latihan 1

Tentukan limit lateral dari fungsi terdefinisi sepotong-sepotong berikut pada titik-titik yang definisinya berubah (x=-2 dan x=4).

Batas lateralnya tidak berimpit di titik x=-2, di sebelah kiri fungsinya cenderung ke arah f(x)=5 dan sebaliknya di sebelah kanan fungsinya konstan dan bernilai 3.

Batas sisinya juga berbeda ketika x mendekati 4. Fungsi sepotong-sepotong mendekati 3 dari kiri, namun mendekati -2 dari kanan.

Latihan 2

Tentukan apakah limitnya ada ketika x mendekati 3 dari fungsi sepotong-sepotong berikut, dan jika ya, berapa nilainya.

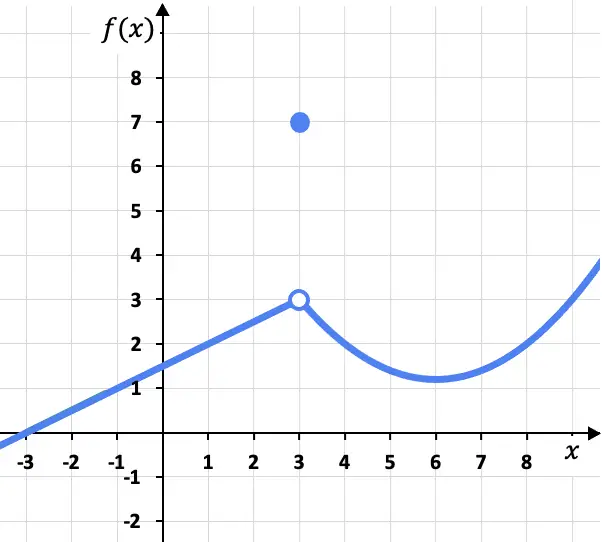
Dalam soal ini, batas lateral di titik x=3 dari kiri dan kanan adalah sama, karena fungsinya cenderung ke arah nilai yang sama (f(x)=3) baik didekati dari kiri maupun dari kanan . sisi kanannya:

Oleh karena itu, menurut definisi matematis dari limit, limit fungsi ketika x cenderung 3 sama dengan 3, karena dua limit lateral pada titik yang sama berimpit pada nilai ini:

Walaupun limit fungsi di x=3 adalah 3, harus diingat bahwa fungsi pada titik ini bukanlah 3, melainkan f(3)=7. Seperti yang akan kita lihat nanti, ini berarti fungsi tersebut tidak kontinu di x=3, melainkan memiliki diskontinuitas yang dapat dihindari.

Latihan 3

Hitung batas lateral fungsi rasional berikut di titik x=4.

Untuk menghitung limit ketika x cenderung ke arah 4 dari kiri, kita ambil nilai yang kurang dari 4 tetapi sangat dekat dengannya, misalnya 3,999:

Jadi limit lateral ketika x mendekati 4 dari kiri adalah ditambah tak terhingga.

Dan untuk menyelesaikan limit ketika x cenderung ke arah 4 dari kanan, kita evaluasi fungsi tersebut pada nilai yang lebih besar dari 4 tetapi sangat dekat dengannya, misalnya 4,001:

Jadi batas lateral x mendekati 4 dari kanan adalah minus tak terhingga.

Latihan 4

Tentukan limit, jika ada, dari fungsi sepotong-sepotong berikut yang ditentukan di titik x=2: