Pada halaman ini kami menjelaskan cara menerapkan aturan Ruffini untuk membagi polinomial. Selain penjelasannya, Anda juga dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah pada pembagian polinomial dengan aturan Ruffini. Selain itu, Anda akan menemukan semua penerapan metode ini dan, faktanya, lebih dari satu aplikasi pasti akan mengejutkan Anda.
Apa aturan Ruffini?
Dalam matematika, aturan Ruffini adalah metode aljabar yang memungkinkan Anda dengan cepat membagi polinomial apa pun dengan polinomial berbentuk xr . Nama aturan Ruffini diambil dari nama ahli matematika Paolo Ruffini, yang menemukan metode ini.
Namun, aturan Ruffini tidak hanya digunakan untuk membagi polinomial, tetapi juga memiliki banyak kegunaan lainnya. Misalnya, aturan Ruffini juga digunakan untuk mencari akar-akar polinomial, mencari nilai numerik suatu polinomial, memfaktorkan suatu polinomial, atau bahkan menyelesaikan persamaan derajat ketiga atau lebih tinggi. Di bawah ini kita akan melihat bagaimana aturan Ruffini diterapkan untuk dapat melakukan semua operasi tersebut.
Terakhir, aturan Ruffini juga dikenal sebagai metode Ruffini, teorema Ruffini, atau pembagian polinomial sintetik.
Bagaimana menerapkan aturan Ruffini
Seperti yang telah kita lihat, kegunaan utama aturan Ruffini adalah membagi polinomial dengan binomial, yaitu membuat pembagian seperti berikut:
![]()
Perhatikan bahwa untuk menggunakan aturan Ruffini , polinomial pembagi harus selalu dibentuk oleh x (dengan koefisien sama dengan 1) dan angka (positif atau negatif), jika tidak maka algoritma Ruffini tidak dapat digunakan.
Untuk menerapkan aturan Ruffini, seluruh prosedur harus diikuti, jadi di bawah ini kita akan menyelesaikan contoh langkah demi langkah untuk melihat bagaimana aturan Ruffini (atau metode Ruffini) diterapkan.
Contoh aturan Ruffini
- Selesaikan pembagian polinomial berikut menggunakan aturan Ruffini:
![]()
Pertama-tama Anda perlu menggambar dua garis tegak lurus yang saling berpotongan, lalu letakkan pembagi dan pembaginya sebagai berikut:
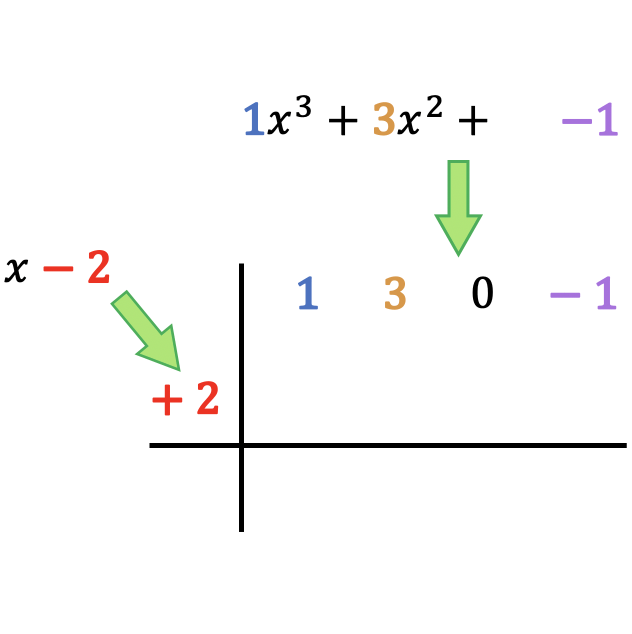
Seperti yang Anda lihat, kita harus meletakkan koefisien polinomial pembagi di atas, diurutkan dari derajat tertinggi hingga terendah, dan kita menempatkan suku bebas dari polinomial pembagi di sebelah kiri kotak dengan perubahan tanda .
Peringatan: Jika polinomial pembagian tidak mempunyai suku derajat tertentu (polinomial tidak lengkap), maka diganti dengan angka 0. Misalnya dalam hal ini polinomial
![]()
Ia tidak mempunyai monomial derajat 1, jadi kita beri angka 0 sebagai gantinya.
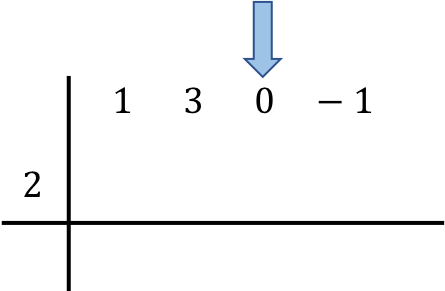
Setelah kita memposisikan polinomial yang terlibat dalam operasi tersebut, kita turunkan angka pertama langsung ke garis di bawah:
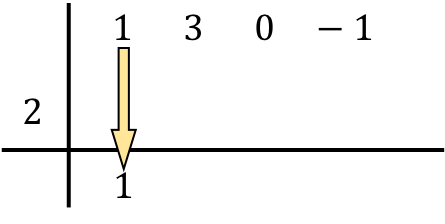
Sekarang sampai pada langkah yang menjadi ciri aturan Ruffini: kita mengalikan angka di bawah dengan angka di sebelah kiri dan menempatkan hasilnya pada kolom berikut :
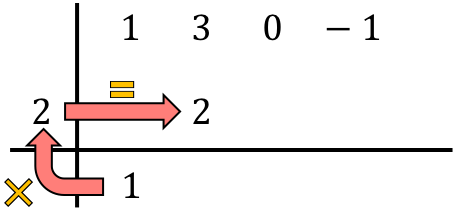
Dan kita menjumlahkan angka-angka pada kolom tersebut, meletakkan hasil penjumlahannya tepat di bawah:
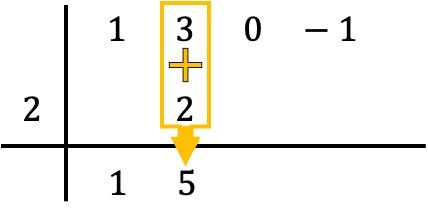
Jadi, metode Ruffini melibatkan pengulangan proses ini. Jadi kita melakukan hal yang sama lagi: kita mengalikan angka terbawah dengan angka di sebelah kiri, kita meletakkan hasilnya di kolom berikutnya dan, terakhir, kita menjumlahkan angka-angka yang disejajarkan secara vertikal:
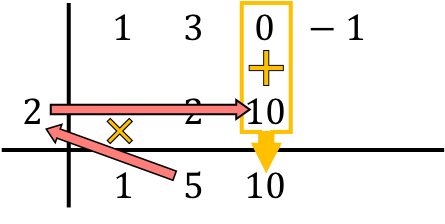
Dan kami mengulangi prosedur yang sama secara berturut-turut hingga akhir. Kita hitung dulu hasil perkalian bilangan di bawah dengan bilangan di sebelah kiri, lalu kita tempatkan hasilnya pada kolom berikutnya dan terakhir kita jumlahkan bilangan-bilangan tersebut pada kolom yang sama:
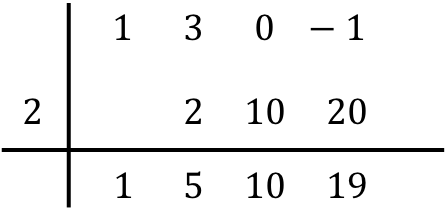
Jadi ketika kita sudah mengisi semua kolomnya, berarti kita sudah selesai membagi polinomialnya.
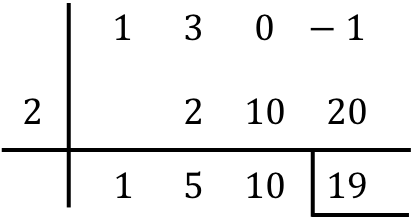
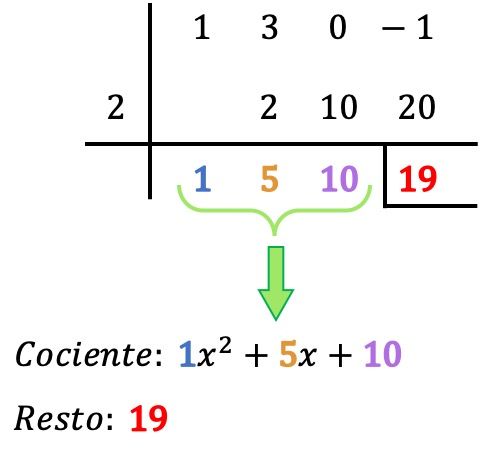
Jadi, Anda hanya perlu mencari hasil pembagian polinomialnya:
- Sisa pembagian antara dua polinomial adalah angka terakhir pada baris di bawahnya, jadi dalam kasus kita, sisanya sama dengan 19. Sisanya biasanya ditunjukkan dengan menempatkan sebuah batang di sebelah kiri dan satu batang lagi di bawah angka tersebut.
- Hasil bagi pembagian polinomial ditentukan oleh nilai-nilai lain yang diperoleh, yaitu koefisien dari hasil bagi polinomial. Digit pertama dari kanan adalah koefisien suku kelas 0, digit berikutnya adalah koefisien suku kelas 1, berikutnya adalah kelas 2, berikutnya adalah kelas 3,… dan seterusnya sampai akhir. . JADI:
Latihan terpecahkan dari aturan Ruffini
Di bawah ini Anda akan menemukan beberapa latihan langkah demi langkah tentang aturan Ruffini sehingga Anda dapat berlatih dan memahami cara menyelesaikan pembagian polinomial dengan metode ini. Kami menyarankan Anda mencoba setiap latihan dan kemudian memeriksa apakah Anda melakukannya dengan benar dengan melihat koreksinya.
Latihan 1
Lakukan pembagian polinomial berikut dengan aturan Ruffini:
![]()
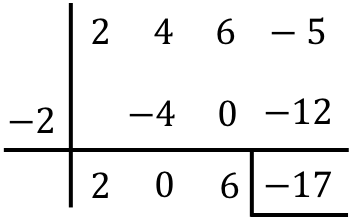
Oleh karena itu, hasil pembagian kedua polinomial tersebut adalah:
Hasil bagi:
![]()
Istirahat:
![]()
Latihan 2
Hitung pembagian polinomial berikut menggunakan aturan Ruffini:
![]()
Dalam kasus khusus ini, polinomial dividen tidak mempunyai suku derajat kedua, oleh karena itu kita harus memberi angka nol pada tempatnya:
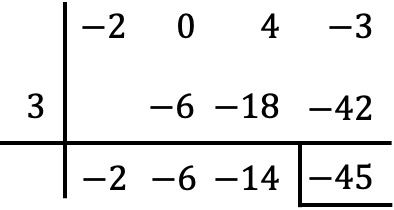
Oleh karena itu, hasil pembagian kedua polinomial tersebut adalah:
Hasil bagi:
![]()
Istirahat:
![]()
Latihan 3
Tentukan hasil pembagian polinomial berikut dengan aturan Ruffini:
![]()
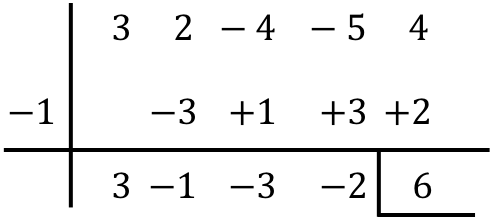
Kesimpulannya, hasil pembagian kedua polinomial tersebut adalah:
Hasil bagi:
![]()
Istirahat:
![]()
Latihan 4
Tentukan nilai m yang belum diketahui sehingga sisa pembagian polinomial berikut setara dengan 5:
![]()
Karena pembaginya berbentuk (xr) atau (x+r), kita dapat menerapkan aturan Ruffini untuk menyelesaikan pembagian tersebut. Oleh karena itu kami menerapkan metode Ruffini dengan menyeret m yang tidak diketahui:
Sekarang kita samakan sisa yang didapat menjadi 5, karena sisanya harus 5:
![]()
Dan kita selesaikan persamaan untuk mencari nilai parameter m :
![]()
![]()
Jadi, jika variabel m setara dengan 3, sisa pembagian antar polinomial akan sama dengan 5.
Latihan 5
Tentukan nilai parameter m sehingga sisa pembagian polinomial berikut menghasilkan 3:
![]()
Karena pembaginya berbentuk (xr) atau (x+r), kita dapat menerapkan aturan Ruffini untuk menyelesaikan pembagian tersebut. Oleh karena itu, kami menggunakan metode Ruffini dengan menyeret m yang tidak diketahui:
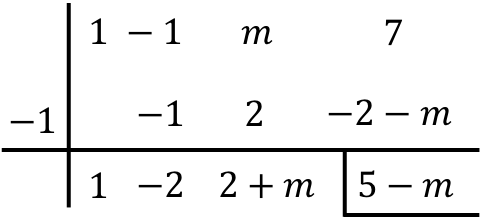
Ingatlah sifat distributif pada perkalian terakhir:
![]()
Sedangkan perhitungan sisa pembagiannya adalah:
![]()
![]()
![]()
Sekarang kita menyamakan ekspresi sisa yang dihasilkan dengan 3, karena sisa pembagian harus sama dengan 3:
![]()
Dan kami menyelesaikan persamaan yang dihasilkan untuk menentukan nilai parameter m :
![]()
![]()
![]()
![]()
Oleh karena itu, m harus sama dengan 2 agar sisa pembagian polinomial sama dengan 3.
Lebih banyak penerapan aturan Ruffini
Seperti yang telah dijelaskan, aturan Ruffini terutama digunakan untuk melakukan pembagian antar polinomial. Namun aturan Ruffini juga digunakan untuk melakukan perhitungan lainnya, kita akan lihat masing-masing di bawah.
Akar polinomial
Akar suatu polinomial dapat dengan mudah ditentukan dengan menggunakan aturan Ruffini. Jika Anda belum mengetahui apa itu akar polinomial, mari kita ulas definisinya:
Akar (atau nol) suatu polinomial adalah nilai-nilai yang menghilangkan polinomial tersebut. Atau dengan kata lain, akar-akar suatu polinomial adalah semua nilai yang jika dievaluasi dalam polinomial tersebut mempunyai nilai numerik sama dengan 0.
![]()
Di sisi lain, kita mengetahui berkat teorema sisa bahwa jika nilai numerik suatu polinomial untuk nilai tertentu
![]()
adalah nol, merupakan sisa pembagian polinomial tersebut
![]()
Itu juga harus 0.
![]()
Oleh karena itu, jika Anda menggunakan aturan Ruffini untuk membagi polinomial
![]()
antara polinomial lain dari bentuk tersebut
![]()
kita memperoleh sisa sama dengan 0, artinya
![]()
adalah akar dari polinomial
![]()
Dengan memberikan contoh pasti kita akan lebih memahami:
- Periksa apakah
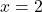
adalah akar dari polinomial
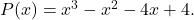
Untuk memeriksa apakah nilai yang diberikan adalah akar polinomial, cukup terapkan metode Ruffini dengan polinomial dan nilai tersebut:
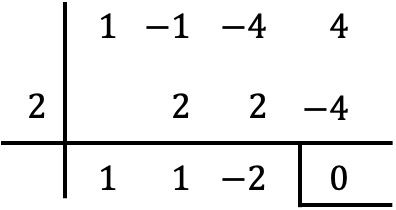
Karena sisa yang diperoleh aturan Ruffini sama dengan nol, berarti efektif
![]()
adalah akar dari polinomial
![]()
Memfaktorkan polinomial
Aturan Ruffini adalah metode yang biasanya diterapkan pada polinomial faktorial, karena memungkinkan Anda mengetahui dengan cepat semua akar polinomial berderajat 3, 4, 5, dst.
Jadi mari kita lihat cara memfaktorkan polinomial dengan algoritma Ruffini menggunakan contoh:
- Faktorkan polinomial derajat ketiga berikut:
![]()
Hal pertama yang harus dilakukan adalah mencari semua akar polinomial. Dan akar-akar yang mungkin dari suatu polinomial adalah pembagi suku bebasnya, yang dalam hal ini adalah 6. Jadi:
Kemungkinan akar polinomial: +1, -1, +2, -2, +3, -3, +6, -6
Sekarang kita perlu mencoba membagi polinomial antara masing-masing nilai tersebut dengan aturan Ruffini. Jika sisa pembagiannya adalah 0, berarti nilainya adalah akar polinomial; namun, jika sisa pembagiannya bukan 0, nilainya bukan merupakan akar polinomial. Jadi, menguji aturan Ruffini dengan semua bilangan hanya membatalkan sisanya dalam tiga kasus berikut:
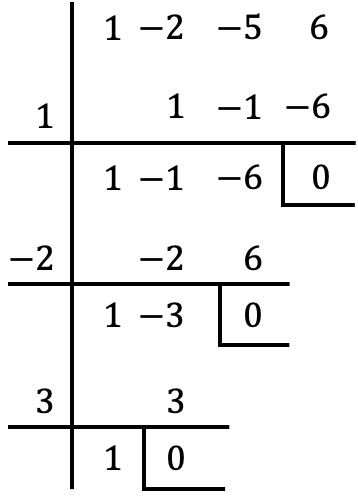
Oleh karena itu, akar-akar polinomial dalam soal adalah nilai-nilai yang menghilangkan sisanya, yaitu:
![]()
Terakhir, untuk memfaktorkan polinomial kita harus menyatakan setiap akar
![]()
dalam bentuk faktor tipenya
![]()
, artinya untuk setiap akar kata Anda harus memberi tanda kurung dengan a
![]()
dan root yang ditemukan telah berubah tanda:
![]()
Seperti yang Anda lihat, kita telah berhasil memfaktorkan polinomial tersebut menggunakan aturan Ruffini. Namun, Anda mungkin ragu dalam memfaktorkan polinomial karena topiknya sangat kompleks. Dalam hal ini Anda dapat mencari di situs web kami (di mesin pencari di kanan atas) untuk artikel yang kami miliki tentang cara memfaktorkan polinomial , di sana kami menjelaskannya lebih detail dan Anda dapat berlatih dengannya latihan yang diselesaikan langkah demi langkah. Selain itu, kami juga menunjukkan metode lain untuk memfaktorkan polinomial.
Hitung nilai numerik polinomial
Meskipun mungkin tampak mengejutkan, nilai numerik suatu polinomial dapat ditentukan dengan aturan Ruffini menggunakan teorema sisa.
Namun yang jelas, untuk melakukan ini Anda perlu mengetahui teorema sisanya. Jika tidak, Anda dapat mencari penjelasan teorema sisa di website kami (di mesin pencari kanan atas) .
Jadi, berkat teorema sisa, kita dapat mengetahui nilai numerik polinomial apa pun. Mari kita lihat cara melakukannya menggunakan contoh:
- Hitung nilai numerik dari

Untuk
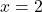
menerapkan aturan Ruffini, menjadi
![]()
Untuk menemukan nilai numerik polinomial untuk nilai tersebut
![]()
Satu-satunya hal yang perlu kita lakukan adalah menggunakan aturan Ruffini dengan polinomial dan nilai tersebut:
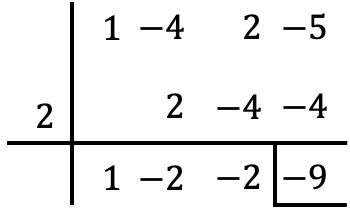
Jadi, dari teorema sisa, kita mengetahui bahwa nilai numerik polinomial tersebut bertepatan dengan sisa pembagian polinomial . Oleh karena itu, nilai numerik polinomial di
![]()
adalah -9.
![]()
Di sisi lain, kita dapat memverifikasi bahwa aturan Ruffini diterapkan dengan benar dengan menghitung nilai numerik secara numerik:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c935b3276a3915dbdf93755851ef28e5_l3.png)
Selesaikan persamaan derajat ketiga atau lebih tinggi
Penerapan lain dari aturan Ruffini adalah untuk menyelesaikan persamaan derajat yang lebih besar dari 2, karena dalam kasus ini tidak ada rumus seperti pada persamaan derajat kedua. Mari kita lihat cara melakukannya menggunakan contoh:
- Selesaikan persamaan kuadrat berikut menggunakan aturan Ruffini:
![]()
Kita perlu memperlakukan persamaan tersebut seolah-olah itu adalah polinomial. Kemudian, kita harus menghitung akar-akar “polinomial” tersebut sebanyak-banyaknya menggunakan aturan Ruffini hingga diperoleh persamaan derajat kedua . Dalam hal ini adalah persamaan derajat 3, oleh karena itu cukup untuk menentukan akar dari “polinomial”:
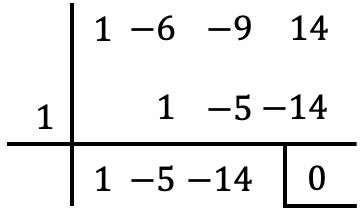
Oleh karena itu, solusi persamaannya adalah
![]()
Nah, untuk mencari solusi lainnya, kita harus menempatkan polinomial yang diperoleh dalam hasil bagi aturan Ruffini sama dengan 0:
![]()
Dan sekarang kita menyelesaikan persamaan kuadrat yang dihasilkan dengan rumus yang sesuai:
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a57aa9f04a1053566c6a53b65afa008a_l3.png)
Kesimpulannya, 3 solusi persamaan derajat ketiga adalah:
![]()