Asimtot horizontal

Pada artikel ini kami menjelaskan apa itu asimtot horizontal suatu fungsi dan cara menghitungnya. Selain itu, Anda akan menemukan beberapa contoh asimtot jenis ini untuk memahami konsep sepenuhnya dan, sebagai tambahan, Anda akan dapat berlatih dengan latihan asimtot horizontal yang diselesaikan.

Apa yang dimaksud dengan asimtot horizontal?

Asimtot horizontal suatu fungsi adalah garis horizontal yang grafiknya mendekati tak terhingga tanpa pernah melintasinya. Oleh karena itu, persamaan asimtot horizontal adalah y=k , dengan k adalah nilai asimtot horizontal.

Artinya, k adalah asimtot horizontal jika limit fungsi ketika x mendekati tak terhingga sama dengan k .

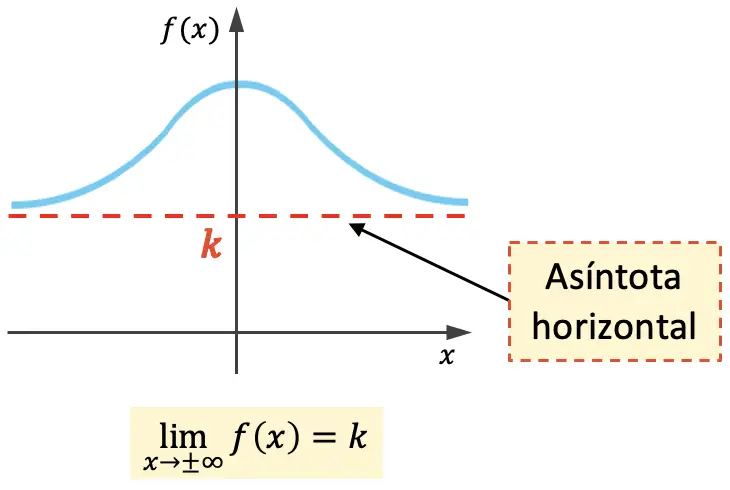
asimtot horizontal suatu fungsi

Fungsi di atas mempunyai asimtot horizontal pada kedua sisi grafiknya, namun suatu fungsi hanya dapat memiliki asimtot horizontal pada salah satu sisinya:

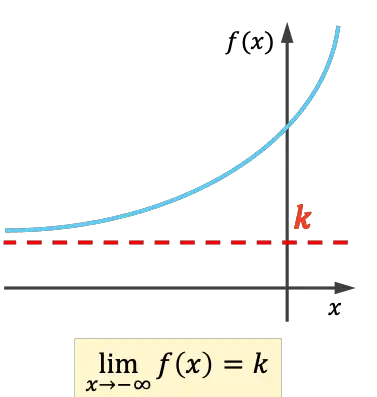
  • Fungsi tersebut mempunyai asimtot horizontal kiri jika limit paling sedikit hingga tak terhingga menghasilkan bilangan real.
  • Fungsi tersebut memiliki asimtot horizontal di sebelah kanan jika limit hingga plus tak terhingga menghasilkan bilangan real.
asimtot horizontal suatu fungsi dari kiri
asimtot horizontal ke kanan

Cara menghitung asimtot horizontal suatu fungsi

Untuk menghitung asimtot horizontal suatu fungsi, langkah-langkah berikut harus diikuti:

  1. Hitung limit fungsi hingga tak terhingga (+∞ dan -∞).
  2. Jika limit hingga tak terhingga menghasilkan bilangan real (k), maka garis y=k merupakan asimtot horizontal dari fungsi tersebut.
  3. Jika tidak ada limit yang bersesuaian dengan bilangan real, maka fungsi tersebut tidak mempunyai asimtot horizontal.

Contoh Asimtot Horisontal

Agar Anda dapat melihat contoh cara melakukannya, kami akan menghapus semua asimtot horizontal dari fungsi rasional berikut:

f(x)=\cfrac{x+1}{x-1}

Untuk menentukan asimtot horizontal, perlu dihitung limit pada minus tak terhingga dan plus tak terhingga dari fungsi tersebut:

\displaystyle \lim_{x \to +\infty} \cfrac{x+1}{x-1} = \cfrac{+\infty}{+\infty}= \cfrac{1}{1} = \bm{1}

\displaystyle \lim_{x \to -\infty} \cfrac{x+1}{x-1} = \cfrac{-\infty}{-\infty}= \cfrac{1}{1} = \bm{1}

➤ Lihat: bagaimana menyelesaikan ketidakterbatasan yang tak terhingga antara yang tak terhingga

Dua limit di tak terhingga menghasilkan 1, jadi y=1 adalah satu-satunya asimtot horizontal dari fungsi tersebut.

Di bawah ini adalah fungsi yang direpresentasikan secara grafis. Seperti yang Anda lihat, fungsinya menjadi sangat dekat dengan y=1 (baik pada plus tak terhingga maupun minus tak terhingga), namun tidak pernah menyentuhnya karena merupakan asimtot horizontal.

contoh asimtot horizontal

Catatan: dalam beberapa kasus khusus, fungsi tersebut memotong asimtot horizontal di satu titik atau lebih, tetapi secara umum grafik suatu fungsi tidak pernah memotong asimtotnya.

Di sisi lain, fungsi ini juga memiliki asimtot vertikal di x=1. Sebab, seperti terlihat pada grafik, garis tersebut sangat dekat dengan garis x=1 tetapi tidak pernah mencapai nilai tersebut.

Memecahkan masalah asimtot horizontal

Latihan 1

Temukan asimtot horizontal, jika ada, dari fungsi pecahan berikut:

\displaystyle f(x)= \frac{4x+3}{2x-1}

Untuk menentukan asimtot horizontal suatu fungsi rasional, perlu dihitung limit tak terhingga dari fungsi tersebut:

\displaystyle \lim_{x \to +\infty} \frac{4x+3}{2x-1} = \frac{4(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{4}{2} = \bm{2}

\displaystyle \lim_{x \to -\infty} \frac{4x+3}{2x-1} = \frac{4(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{4}{2} = \bm{2}

Dalam hal ini, hasil bentuk tak tentu ∞/∞ adalah pembagian koefisien x pangkat tertinggi, karena pembilang dan penyebutnya berorde sama.

Batas pada plus tak terhingga dan minus tak terhingga dari fungsi tersebut menghasilkan 2, jadi y=2 adalah asimtot horizontal dan merupakan satu-satunya asimtot yang dimiliki fungsi tersebut.

Latihan 2

Temukan semua asimtot horizontal dari fungsi rasional berikut yang memiliki akar:

\displaystyle f(x)= \frac{3x}{\sqrt{x^2+2}}

Untuk mencari asimtot horizontal suatu fungsi, pertama-tama kita hitung limit pada tak terhingga positif:

\displaystyle \lim_{x \to +\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{+\infty}{+\infty} = \frac{3}{\sqrt{1}} = \bm{3}

Dan kemudian kita menyelesaikan limit fungsi hingga negatif tak terhingga:

\displaystyle \lim_{x \to -\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{-\infty}{+\infty} = \frac{-3}{\sqrt{1}} = \bm{-3}

➤ Jika Anda ragu tentang cara menyelesaikan batas hingga tak terhingga, kami sarankan untuk memeriksa tautan di atas tentang cara menyelesaikan ketidakpastian tak terhingga di antara tak terhingga.

Dalam hal ini, kami memperoleh dua nilai batas tak terhingga yang berbeda. Oleh karena itu, fungsi tersebut mempunyai dua asimtot horizontal: y=3 adalah asimtot horizontal dari fungsi di sebelah kanan dan, sebaliknya, y=-3 adalah asimtot horizontal dari fungsi di sebelah kiri.

Latihan 3

Hitung asimtot horizontal dari fungsi terdefinisi sepotong-sepotong berikut ini:

\displaystyle f(x)=\left\{ \begin{array}{lcl}\displaystyle\frac{3x-1}{x^2}& \text{si} & x<4\\[4ex]\displaystyle\frac{x^3-2x+5}{2x^3-9} & \text{si} & x\geq 4 \end{array} \right.

Untuk menghitung asimtot horizontal suatu fungsi, tidak ada rumusnya, tetapi Anda harus menghitung batas plus dan minus tak terhingga.

Jadi, untuk mencari batas minimal tak terhingga, kita ambil fungsi yang ditentukan di bagian pertama:

\displaystyle \lim_{x \to -\infty}\frac{3x-1}{x^2}= \frac{-\infty}{+\infty}=\bm{0}

Jadi garis y=0 merupakan asimtot horizontal di sebelah kiri fungsi.

Dan sekarang kita menghitung limit pada plus tak terhingga dengan mengambil fungsi yang ditentukan di bagian kedua:

\displaystyle \lim_{x \to +\infty}\frac{x^3-2x+5}{2x^3-9}= \frac{+\infty}{+\infty}=\mathbf{\frac{1}{2}}

Jadi garis y=1/2 adalah asimtot horizontal di sebelah kanan fungsi tersebut.

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top