Apa itu vektor (matematika)? -Matoritas

Di halaman ini, Anda akan menemukan segala sesuatu tentang vektor: apa itu vektor, ciri-cirinya, cara menghitungnya, cara melakukan operasi dengan vektor, macam-macam jenis yang ada,…

Apa itu vektor?

Definisi matematis suatu vektor adalah sebagai berikut:

Dalam matematika, vektor adalah segmen berarah yang berpindah dari satu titik (disebut titik asal) ke titik lain (disebut titik akhir).

Misalnya pada grafik di bawah ini, Anda dapat melihat vektor tersebut

$\vv{AB}$

Ia memiliki titik A sebagai titik asal dan titik B sebagai titik akhirnya.

Vektor terutama digunakan dalam matematika, khususnya geometri, dan fisika, untuk merepresentasikan gaya vektor secara grafis.

Ciri-ciri suatu vektor

Setelah kita mengetahui apa arti matematis dari vektor, sekarang mari kita lihat apa saja sifat-sifatnya.

Setiap vektor mempunyai ciri-ciri geometri sebagai berikut:

Arah : Arah suatu vektor adalah arah garis yang memuat vektor tersebut atau garis apa pun yang sejajar dengannya. Dengan kata lain, arah suatu vektor adalah garis tempat vektor itu berada.
Arah : arah suatu vektor adalah orientasi vektor tersebut, yang ditunjukkan oleh panahnya.
Modul (atau besaran): modul suatu vektor adalah panjangnya, dan sesuai dengan nilai numerik vektor tersebut. Oleh karena itu, semakin besar arti vektornya, semakin besar pula besaran vektor yang diwakilinya.
Titik penerapan : titik penerapan suatu vektor adalah titik asal vektor tersebut.

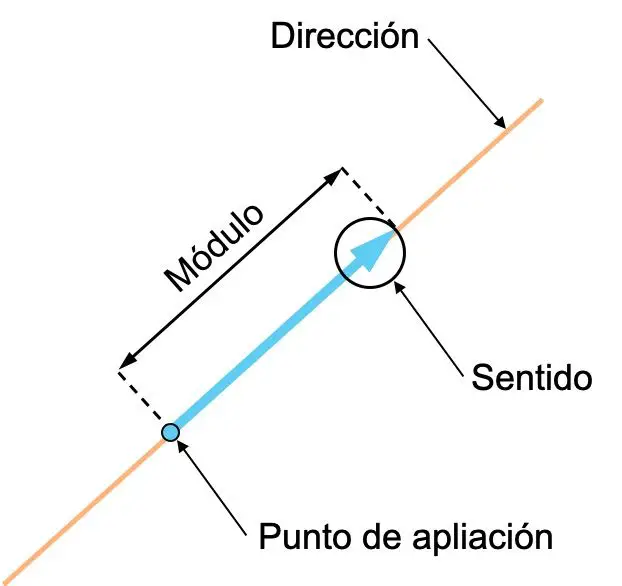
Pengertian arah dan arah suatu vektor seringkali membingungkan, sehingga penting untuk membedakan keduanya. Perhatikan contoh dua vektor berikut, keduanya mempunyai arah yang sama tetapi artinya berbeda:

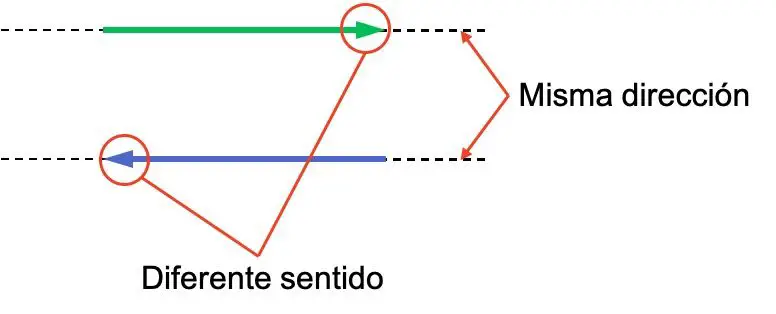
Kedua vektor mempunyai arah yang sama karena sejajar. Sebaliknya arahnya berlawanan karena menghadap ke belakang.

Komponen vektor

Kita baru saja melihat bahwa vektor direpresentasikan secara grafis dengan panah, namun vektor juga dapat direpresentasikan secara numerik dengan komponen (atau koordinat) dari sebuah vektor.

Misalnya, jika kita mempunyai vektor berikut yang direpresentasikan dalam grafik:

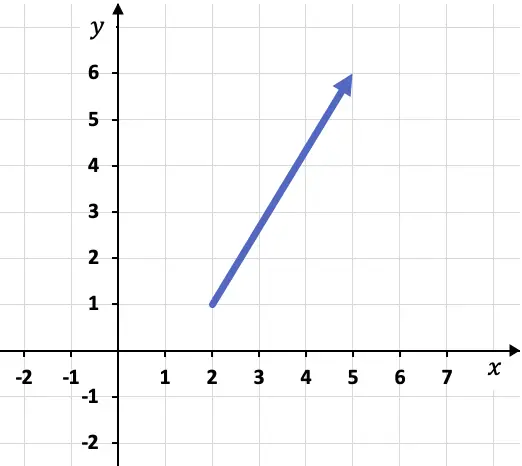
Untuk menghitung komponen-komponen suatu vektor, terlebih dahulu kita harus mengetahui koordinat asal dan akhirnya, yaitu titik awal dan akhir. Dalam hal ini, titik asal dan akhir vektor adalah:

Asal vektor: A(2,1)

Titik akhir vektor: B(5,6)

Jadi, untuk mencari koordinat atau komponen vektor, cukup kurangi titik akhir dikurangi titik asal:

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

Sehingga komponen-komponen vektor yang terwakili dalam grafik adalah:

$\vv{\bm{AB}}\bm{=(3,5)}$

Operasi vektor

menambahkan vektor

Untuk menjumlahkan dua vektor secara numerik, Anda harus menjumlahkan masing-masing komponennya. Atau dengan kata lain koordinat X kedua vektor dijumlahkan dan sama dengan koordinat Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

Agar Anda dapat melihat bagaimana hal ini dilakukan, kami akan menambahkan dua vektor berikut:

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

Dua vektor juga dapat ditambahkan dari representasi grafisnya. Untuk ini, aturan atau hukum jajaran genjang biasanya digunakan, namun ada banyak metode. Anda dapat melihat contoh dan latihan yang diselesaikan tentang cara menjumlahkan dua vektor secara grafis di sini.

pengurangan vektor

Untuk mengurangkan dua vektor secara analitis, Anda harus mengurangkan masing-masing komponennya. Artinya, koordinat X kedua vektor tersebut dikurangkan satu sama lain dan sama dengan koordinat Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

Sebagai contoh, kita akan mengurangkan dua vektor berikut:

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

Seperti penjumlahan, Anda juga dapat mengurangkan 2 vektor menggunakan representasinya. Untuk ini biasanya digunakan aturan atau hukum segitiga, tetapi ada beberapa metode. Anda dapat melihat semuanya dengan contoh dan latihan yang diselesaikan tentang cara mengurangi dua vektor secara grafis .

modul vektor

Seperti yang kita lihat di awal halaman ini, besaran suatu vektor sama dengan panjang vektor tersebut. Nah, panjang (atau besaran) suatu vektor dapat ditentukan dari komponen-komponennya.

Pertimbangkan vektor apa pun:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Untuk mencari besar suatu vektor pada bidang, kita harus menerapkan rumus berikut:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

Misalnya kita akan menghitung besar vektor berikut dengan menggunakan rumus:

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

Meskipun kelihatannya sangat sederhana, menentukan besaran suatu vektor bisa jadi rumit. Jika Anda ingin melihat lebih banyak contoh dan latihan dengan latihan yang diselesaikan dari modul vektor , kami menyarankan Anda mengunjungi halaman tertaut ini.

Perkalian vektor dengan skalar

Untuk menghitung secara numerik hasil kali suatu vektor dengan suatu bilangan (atau skalar), setiap komponen vektor harus dikalikan dengan bilangan tersebut.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

Dalam contoh umum berikut, Anda dapat melihat bagaimana arah vektor dipertahankan, apa pun tanda skalarnya. Sebaliknya, arah vektor bergantung pada tanda bilangan yang dikalikan.

perkalian atau hasil kali suatu bilangan atau skalar dengan suatu vektor

Di bawah ini Anda dapat melihat contoh numerik cara mencari hasil kali vektor dan bilangan:

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

Produk skalar

Dalam geometri analitik, perkalian titik adalah operasi vektor yang mengalikan dua vektor dan mengubahnya menjadi bilangan real.

Jadi, rumus perkalian titik dua vektor adalah sebagai berikut:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

Di bawah ini Anda memiliki contoh penghitungan hasil perkalian titik antara dua vektor:

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

Di tautan ini Anda dapat melihat lebih banyak contoh perkalian titik . Selain itu, Anda akan menemukan cara lain untuk mencari perkalian titik antara dua vektor, sifat-sifat jenis operasi dengan vektor dan latihan yang diselesaikan langkah demi langkah.

produk vektor

Meskipun namanya sangat mirip, perkalian titik dan perkalian silang sangatlah berbeda.

Perkalian silang , disebut juga perkalian silang, adalah operasi antara dua vektor dalam ruang (dalam R3), yaitu vektor-vektor tiga koordinat.

Jadi, jika kita mempunyai dua vektor tiga dimensi:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Perkalian silang kedua vektor sama dengan hasil determinan 3×3 berikut:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

dimana vektornya

$\vv{i}, \vv{j},\vv{k}$

adalah vektor satuan yang masing-masing searah sumbu X, Y, Z.

Selain itu, arah vektor yang dihasilkan adalah tegak lurus terhadap dua vektor yang dikalikan.

Seperti yang bisa Anda tebak, menyelesaikan jenis operasi ini lebih sulit daripada yang sebelumnya dan, oleh karena itu, kami memiliki satu halaman penuh dengan penjelasan mendetail tentang cara menghitung perkalian silang antara dua vektor. Oleh karena itu, jika Anda tertarik, kami menyarankan Anda mengunjunginya dan berlatih dengan latihan perkalian vektor yang diselesaikan .

produk campuran

Perkalian campuran tiga vektor, disebut juga perkalian tiga titik, adalah perkalian berurutan antara tiga vektor yang melibatkan dua jenis operasi berbeda: perkalian titik dan perkalian vektor. Jadi, kombinasi kedua operasi vektor menghasilkan skalar (bilangan real).

Konkretnya, perkalian campuran terdiri dari penghitungan perkalian vektor dari dua vektor dan selanjutnya mengalikan hasil yang diperoleh secara vektor dengan vektor ketiga. Lihatlah rumusnya:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

Seperti halnya perkalian vektor, menyelesaikan perkalian campuran antar vektor tidaklah mudah. Oleh karena itu, kami menyarankan Anda untuk melihat penjelasan tentang hasil kali campuran tiga vektor ini, di mana Anda akan menemukan contoh, latihan yang diselesaikan, dan arti geometri dari operasi vektor ini.

jenis vektor

Ada banyak jenis vektor, namun definisi yang paling penting untuk diketahui adalah:

Vektor satuan : vektor yang modulusnya sama dengan 1.
Vektor tetap : Suatu vektor menjadi tetap jika titik asal vektor diterapkan pada suatu titik tetap.
Vektor bebas : Suatu vektor dikatakan bebas jika titik penerapannya tidak ditentukan, tetapi merupakan titik bebas.
Vektor-vektor yang segaris : dua buah vektor atau lebih dikatakan segaris jika vektor-vektor tersebut mempunyai garis aksi yang sama (garis tempat vektor tersebut berada).
Vektor-vektor ekuivalen : dua buah vektor disebut ekipolen jika keduanya mempunyai ukuran yang sama, pengertian yang sama, dan arah yang sama (walaupun titik penerapannya dapat berbeda).
Vektor tertaut : Vektor tertaut adalah vektor ekuipolen yang juga bekerja pada garis yang sama.
Vektor Berlawanan : dua buah vektor yang berlawanan jika besarnya sama dan arahnya sama, tetapi arahnya berbeda.
Vektor posisi : vektor posisi adalah vektor yang asal mulanya adalah titik (0,0) (asal koordinat).
Vektor-vektor yang bersaing : dua atau lebih vektor-vektor adalah konkuren jika garis-garis aksinya melalui titik yang sama, yaitu berpotongan.
Vektor sejajar : dua vektor atau lebih sejajar jika arahnya sama, berapapun arahnya.
Vektor tegak lurus : Dua vektor tegak lurus (atau ortogonal) jika arahnya membentuk sudut 90º.
Vektor ortonormal : Dua atau lebih vektor dikatakan ortonormal jika vektor-vektor tersebut saling tegak lurus dan terlebih lagi kesatuan (besarnya sama dengan satu).
Vektor koplanar : dua vektor atau lebih adalah koplanar bila berada pada bidang yang sama.

Sudut antara dua vektor

Untuk mencari sudut antara dua vektor tertentu, kita harus menerapkan rumus berikut:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Emas

$\lvert \vv{\text{u}} \rvert$

Dan

$\lvert \vv{\text{v}} \rvert$

adalah modul dari vektor

$\vv{\text{u}}$

Dan

$\vv{\text{v}}$

masing-masing.