Pada halaman ini Anda akan menemukan penjelasan tentang apa saja komponen (atau koordinat) suatu vektor. Selain itu, Anda juga akan dapat melihat cara penghitungannya dari dua titik dan bahkan cara penguraiannya melalui modul dan sudutnya. Selain itu, Anda akan menemukan contoh dan latihan yang diselesaikan langkah demi langkah.
Apa saja komponen vektor?
Komponen suatu vektor adalah proyeksi suatu vektor pada sumbu kartesius. Oleh karena itu, proyeksi vektor ke sumbu x adalah komponen X dari vektor tersebut dan demikian pula proyeksi vektor ke sumbu y adalah komponen Y dari vektor tersebut.
Komponen-komponen suatu vektor dapat juga disebut koordinat suatu vektor.
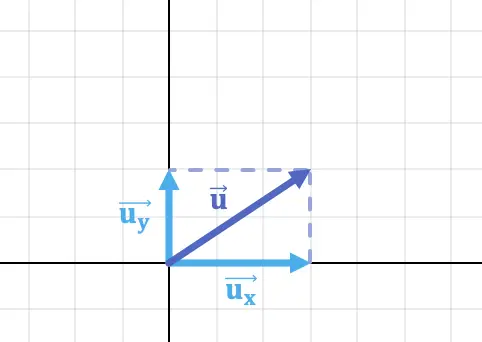
Misalnya komponen horizontal dan komponen vertikal vektor pada gambar di atas adalah:
![]()
![]()
Jadi vektornya adalah:
![]()
Oleh karena itu, komponen suatu vektor juga dapat didefinisikan sebagai representasi suatu vektor dalam suatu sistem koordinat. Jelasnya, jika suatu sistem dua dimensi (dalam r2) vektornya akan mempunyai dua komponen, sebaliknya jika suatu basis tiga dimensi (dalam r3) vektornya akan terdiri dari tiga komponen.
Komponen kartesius suatu vektor sangat penting karena dengan komponen tersebut kita dapat mengetahui ciri-ciri suatu vektor, yang terutama adalah arah, sense, dan modulus (atau besaran) vektor tersebut. Selain itu, mereka digunakan untuk melakukan operasi vektor.
Cara menghitung komponen vektor dari dua titik
Kita baru saja melihat cara mencari koordinat suatu vektor secara grafis, namun kita juga dapat menentukan komponen-komponennya secara numerik.
Untuk menghitung secara numerik komponen-komponen suatu vektor, kita perlu mengetahui dua titik: asal dan akhirnya, atau dengan kata lain, di mana ia dimulai dan di mana ia berakhir. Karena komponen suatu vektor adalah koordinat yang diperoleh dengan mengurangkan ujung vektor dikurangi titik asal.
![]()
Misalnya, kita akan menghitung vektor yang asal titik A(3,1) dan ujungnya adalah titik B(5,4):
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{AB} & = (5,4)-(3,1) \\[1.5ex] &= (5-3,4-1) \\[1.5ex] & = \bm{(2,3)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c740536015a29149532a4a1eb46f4f7_l3.png)
Seperti yang Anda lihat, menentukan komponen suatu vektor tidaklah terlalu sulit, namun ini cukup penting. Misalnya, salah satu jenis vektor yang paling umum digunakan adalah vektor tegak lurus (atau ortogonal); Nah, jika Anda sudah memahami apa itu koordinat suatu vektor, maka sangat mudah untuk menghitung vektor yang tegak lurus. Anda dapat melihat caranya pada penjelasan vektor ortogonal .
Cara menghitung komponen suatu vektor dari modulus dan sudutnya
Anda juga dapat mengetahui komponen suatu vektor dari besarnya dan sudutnya terhadap sumbu X. Proses ini disebut dekomposisi vektor .
Jadi, komponen X dan Y dari vektor dapat dihitung dengan perbandingan trigonometri kosinus dan sinus:

Seperti terlihat pada gambar, modulus suatu vektor dan komponen-komponennya melengkapi segitiga siku-siku, sehingga rumus dasar trigonometri dapat diterapkan.
Jika Anda tidak ingat cara menghitung modulus suatu vektor, Anda dapat mencari tahu apa itu modulus suatu vektor . Di sini Anda akan menemukan rumus besaran vektor, serta contoh, latihan langkah demi langkah, dan semua sifat besaran vektor. Ini penjelasannya sangat lengkap sehingga anda akan memahaminya dengan sempurna. ✅
Berbeda dengan besaran suatu vektor yang selalu positif, komponen-komponennya bisa negatif karena sinus dan kosinusnya bisa bernilai negatif.
Sebagai contoh, kita akan melakukan dekomposisi vektor dari vektor yang modulus dan sudutnya dengan sumbu OX adalah:
![]()
Komponen X dari vektor sama dengan modulus dikalikan dengan kosinus sudut:
![]()
Dan komponen Y dari vektor sama dengan hasil kali modul dan sinus sudut:
![]()
Jadi koordinat vektornya adalah:
![]()