Anda pasti pernah mendengar tentang himpunan bilangan imajiner atau satuan imajiner. Ini adalah konsep matematika yang muncul dari kebutuhan matematika untuk menyatakan bilangan yang bukan milik bilangan real .
Apa itu bilangan imajiner?
Bilangan imajiner adalah bilangan yang jika dikuadratkan akan menghasilkan bilangan negatif . Oleh karena itu, ini adalah nilai yang setara dengan akar kuadrat dari bilangan negatif. Misalnya, satuan imajiner (angka i) sama dengan akar kuadrat -1.
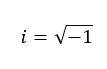
Bilangan-bilangan ini bukan termasuk bilangan riil, karena pada himpunan riil akar-akar negatif tidak dapat diselesaikan. Di sinilah letak pentingnya setting imajiner. Himpunan ini diciptakan untuk dapat menangani akar-akar negatif dan untuk dapat menyelesaikan semua persamaan dan permasalahan kuadrat yang “tidak mempunyai penyelesaian”, karena keduanya memberikan kita akar negatif.
Untuk menghindari kebingungan, penting untuk membedakan bilangan imajiner dan bilangan kompleks . Kompleks adalah bilangan yang terdiri dari bilangan real dan bilangan imajiner . Oleh karena itu, imajinasi adalah subkategori kompleks yang tidak memiliki bagian nyata. Pada tabel berikut Anda akan dapat lebih memahami perbedaannya.
| bilangan kompleks | pesta kerajaan | bagian imajinasi | Keterangan |
| 4+7i | 4 | 7i | Kompleks |
| 3 | 3 | 0 | kerajaan murni |
| 2i | 0 | 2i | Imajinasi Murni |
Untuk menyelesaikan penempatan himpunan digital ini, kita dapat memvisualisasikan pada gambar berikut struktur semua himpunan. Seperti yang bisa kita lihat, bilangan kompleks mencakup semua jenis bilangan , yang pada gilirannya dapat dibagi menjadi bilangan real dan bilangan imajiner murni (yang akan kita bahas dalam artikel ini).

Contoh Bilangan Imajiner
Dari satuan imajiner (i), kita dapat menyimpulkan bilangan imajiner lainnya. Anda hanya perlu menerapkan rumus berikut:
m = ri
Dimana m adalah bilangan imajiner, r adalah bilangan real, dan i adalah satuan imajiner. Pada gambar berikut Anda dapat melihat bagaimana kita mendapatkan imajinasi yang berbeda dari akar negatif.
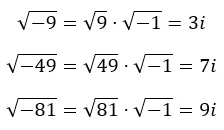
Faktanya, kita dapat mengekstrapolasinya ke ekspresi berikut:
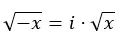
Sifat-sifat bilangan imajiner
Bilangan imajiner mempunyai sejumlah sifat yang sangat menarik . Beberapa sudah kami bicarakan di awal artikel ini dan lainnya belum:
- Imajiner tidak termasuk dalam himpunan realitas, karena imajinasi adalah angka-angka yang secara fisik tidak ada dan tidak dapat direpresentasikan dalam realitas kita.
- Ini adalah nilai yang setara dengan akar negatif.
- Mereka dapat direpresentasikan secara grafis pada garis imajiner.
- Pangkat imajiner (ini adalah konsep yang akan kami jelaskan di bagian selanjutnya) sangat membantu dalam menyederhanakan penghitungan numerik yang melibatkan nilai imajiner.
- Rumus Euler adalah ekspresi yang memungkinkan Anda menghubungkan bilangan imajiner dengan bilangan real.
Operasi dengan bilangan imajiner
Sekarang setelah Anda mengetahui semua karakteristik penting bilangan imajiner, sekarang saatnya mempelajari cara menyelesaikan operasi bilangan imajiner. Untuk mengoperasikan nilai imajiner , Anda harus mengikuti langkah yang sama seperti yang Anda ikuti untuk mengoperasikan nilai nyata, kecuali Anda harus mempertimbangkan satu konsep: kekuatan imajiner.
kekuatan imajinatif
Bilangan imajiner memiliki sifat yang sangat menarik yang terjadi ketika Anda mengalikan satuan imajiner dengan bilangan itu sendiri. Artinya, ini terjadi ketika Anda membuat kekuatan kesatuan imajiner . Jika kita menuliskan pangkat-pangkatnya, seperti pada daftar berikut, kita dapat menemukan suatu pola:
saya 0 = 1
saya 1 = saya
saya 2 = saya · saya = ( √ -1) · ( √ -1) = -1
saya 3 = saya 2 saya = (-1) saya = -i
saya 4 = saya 2 saya 2 = (-1) (-1) = 1
Mengetahui konsep ini akan memudahkan kita dalam menyelesaikan operasi bilangan imajiner, karena kita akan dapat menyederhanakan operasi yang sulit dan membuatnya sedikit lebih mudah. Selain itu, hal baiknya tentang kekuatan ini adalah bahwa kekuatan tersebut berulang tanpa batas. Kita dapat melihat ini, jika kita menambahkan beberapa kekuatan lagi:
saya 5 = saya
saya 6 = -1
saya 7 = -i
saya 8 = 1
dll.
Dan dengan kekuatan negatif, hal ini juga terjadi.
Operasi aritmatika dengan bilangan imajiner
Selanjutnya, kami akan memberikan contoh setiap operasi aritmatika dasar, sehingga Anda dapat melihat penyelesaian perhitungan bilangan imajiner.
- Menjumlahkan bilangan imajiner: sama persis dengan menjumlahkan bilangan real, hanya saja jangan lupa menambahkan i.
4i + 3i = 7i
- Pengurangan bilangan imajiner: Pengurangan juga diselesaikan dengan cara yang sama seperti pada himpunan nyata.
4i – 3i = saya
- Perkalian bilangan imajiner: dalam hal ini kita harus mengingat pangkat imajiner yang telah kita sebutkan sebelumnya.
3i 4i = 12 i 2 = 12 (-1) = -12
- Pembagian bilangan imajiner: pada pembagian jenis ini kita juga harus waspada, jika kita menemui kekuatan imajiner, yang memungkinkan kita menyederhanakan operasinya.
12i 4i = 3
Persamaan dengan bilangan imajiner
Seperti yang kami katakan sebelumnya, ketika kita menyelesaikan persamaan di himpunan nyata, terkadang kita mendapatkan akar-akar negatif dan, oleh karena itu, persamaan tersebut “tidak memiliki solusi” . Namun, setelah kita mengetahui imajinasinya, kita bisa menyelesaikan persamaan ini. Mari kita lihat contohnya:
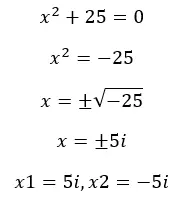
Untuk apa bilangan imajiner digunakan?
Bilangan imajiner muncul dari kebutuhan untuk dapat menyatakan nilai-nilai yang berada di luar himpunan sebenarnya. Itu sebabnya, pada awalnya, sepertinya mereka tidak memiliki banyak aplikasi yang berguna . Namun kenyataannya justru sebaliknya. Karena jika kita gabungkan dengan bilangan real, kita mendapatkan bilangan kompleks.
Dan ini memiliki banyak penerapan. Mereka digunakan untuk mempelajari arus bolak-balik (karena mempunyai nilai negatif), penggunaannya juga sangat luas di bidang gelombang (yang mempunyai aplikasi dalam fisika, elektronik telekomunikasi dan mekanika kuantum). Di antara banyak kegunaan lainnya.
Selain itu, sering kali saat Anda menyelesaikan persamaan kuadrat , nilainya memberi Anda akar negatif dan Anda tidak dapat mengoperasikannya… Dengan imajinasi Anda dapat menyelesaikannya . Jadi, sebagai kesimpulan, kita dapat mengatakan bahwa ini adalah himpunan yang memungkinkan kita memperluas pengetahuan kita yang lebih abstrak.