Halaman ini menjelaskan arti titik tengah suatu segmen. Selain itu, Anda akan menemukan cara mencari titik tengah suatu ruas menggunakan rumusnya. Anda bahkan akan melihat contoh, latihan, dan penyelesaian masalah titik tengah segmen.
Berapakah titik tengah suatu segmen?
Dalam matematika, titik tengah suatu ruas adalah titik yang terletak pada jarak yang sama dari titik ujung suatu ruas. Oleh karena itu, bagian tengah membagi segmen menjadi dua bagian yang sama.
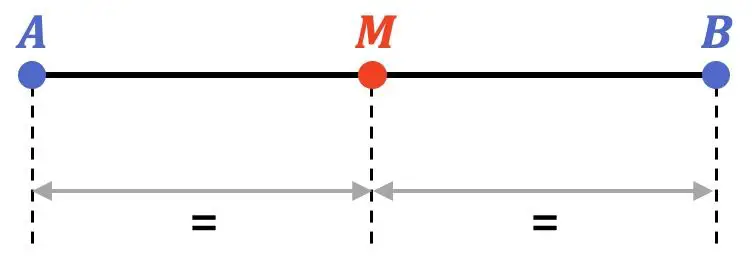
Selain itu, titik tengahnya berada tepat di tengah-tengah ruas, sehingga termasuk dalam garis bagi ruas tersebut.
Sebaliknya, titik tengah suatu ruas juga merupakan titik yang berjarak sama dari dua elemen geometri: kedua ujung ruas tersebut.
Bagaimana cara menghitung titik tengah suatu segmen?
Diketahui koordinat Cartesius dari titik-titik ekstrim suatu segmen:
![]()
Koordinat titik tengah ruas tersebut sesuai dengan setengah jumlah koordinat titik ekstrim:
![]()
Ini adalah rumus titik tengah suatu ruas pada bidang kartesius (di R2). Namun yang jelas rumus tersebut juga berlaku untuk ruang kartesius (di R3), Anda hanya perlu menjumlahkan setengah jumlah koordinat Z:
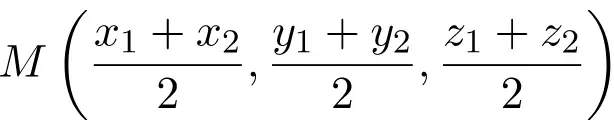
Mari kita lihat contoh cara menghitung koordinat titik tengah suatu segmen:
- Tentukan titik tengah segmen yang dibentuk oleh titik-titik berikut:
![]()
Untuk mencari titik tengah ruas, cukup terapkan rumusnya:
![]()
![]()
![]()
![]()
Latihan diselesaikan di tengah-tengah segmen
Latihan 1
Berapakah titik tengah ruas garis yang titik ujungnya pada dua titik berikut?
![]()
Untuk mencari titik tengah ruas harus langsung menerapkan rumus:
![]()
![]()
![]()
![]()
Latihan 2
Tentukan koordinat titik ujung ruas yang bermula di titik A dan titik tengahnya M.
![]()
Dalam hal ini kita mengetahui koordinat titik awal dan titik tengah ruas. Oleh karena itu, kita substitusikan koordinat yang kita ketahui ke dalam rumus titik tengah suatu segmen:
![]()
![]()
Dan sekarang kita menyelesaikan koordinat titik akhir segmen dari persamaan sebelumnya:
koordinat X
![]()
![]()
![]()
![]()
![]()
koordinat Y
![]()
![]()
![]()
![]()
![]()
Oleh karena itu, koordinat ujung akhir segmen tersebut adalah:
![]()
Latihan 3
Diketahui jajar genjang berikut:
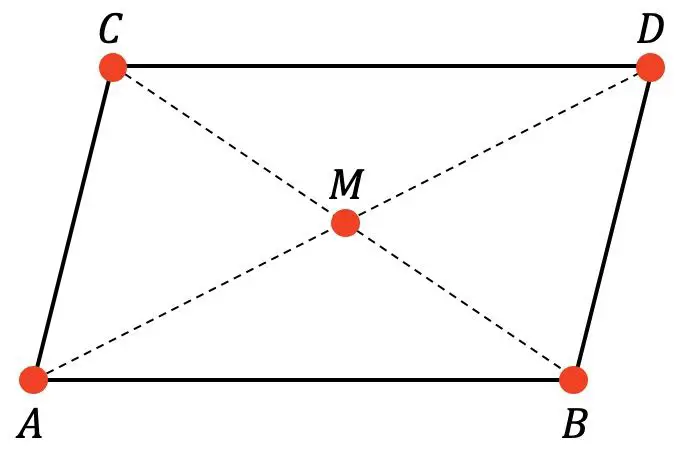
Diketahui M adalah pusat jajar genjang dan koordinat titik A, B, dan C adalah:
![]()
Dari informasi ini dan menggunakan rumus titik tengah, hitung koordinat titik D.
Untuk mencari koordinat titik D menggunakan rumus titik tengah suatu ruas, pertama-tama kita harus menghitung koordinat titik M, kemudian koordinat titik D.
Titik M adalah titik tengah ruas BC, maka koordinatnya adalah:
![]()
![]()
Dan setelah kita mengetahui titik M, maka kita dapat menemukan titik D. Titik M juga merupakan titik tengah ruas AD, jadi:
![]()
Koordinat X titik D
![]()
![]()
![]()
Koordinat Y titik D
![]()
![]()
![]()
Maka koordinat titik D adalah:
![]()
Latihan 4
Hitung persamaan kontinu garis yang tegak lurus ruas PQ di titik tengahnya. Jadilah poinnya
![]()
Dan
![]()
Untuk menentukan persamaan suatu garis, kita memerlukan vektor arahnya dan sebuah titik yang merupakan bagian dari garis tersebut.
Dalam hal ini, vektor arah garis akan tegak lurus terhadap vektor tersebut
![]()
Oleh karena itu kami menghitung vektornya
![]()
![]()
Dan kita dapat mencari suatu vektor yang tegak lurus terhadap vektor lain dengan mengubah komponen-komponen vektor di antara vektor-vektor tersebut kemudian mengubah tanda suatu komponen, oleh karena itu:
![]()
Kita sekarang mempunyai vektor arah garis, jadi kita hanya memerlukan satu titik yang termasuk dalam garis tersebut. Dalam hal ini, instruksi memberitahu kita bahwa garis melewati titik tengah segmen, jadi kita menghitung titik tengahnya menggunakan rumus:
![]()
![]()
Terakhir, kita buat persamaan garis kontinu dari titik dan vektor yang dihitung:
![]()