Pada halaman ini Anda akan menemukan penjelasan tentang apa yang dimaksud dengan kombinasi linier antar vektor. Selain itu, Anda akan dapat melihat contoh bagaimana vektor dinyatakan sebagai kombinasi linier dan, sebagai tambahan, Anda akan dapat berlatih dengan latihan dan soal yang diselesaikan langkah demi langkah.
Apa yang dimaksud dengan kombinasi linier vektor?
Pengertian kombinasi linier adalah sebagai berikut:
Kombinasi linier suatu himpunan vektor adalah vektor yang diperoleh dengan menjumlahkan seluruh vektor pada himpunan tersebut dikalikan skalar (bilangan real).
Dengan kata lain, diberikan himpunan vektor
![]()
kombinasi liniernya adalah:
![]()
Dimana koefisiennya
![]()
Ini adalah bilangan real.
Oleh karena itu, vektor yang merupakan kombinasi linier dari vektor-vektor lain berarti vektor pertama dapat dinyatakan dalam vektor kedua.
Konsep ini dapat lebih dipahami dengan membuat grafik sebuah vektor pada bidang yang merupakan kombinasi linier dari dua vektor:
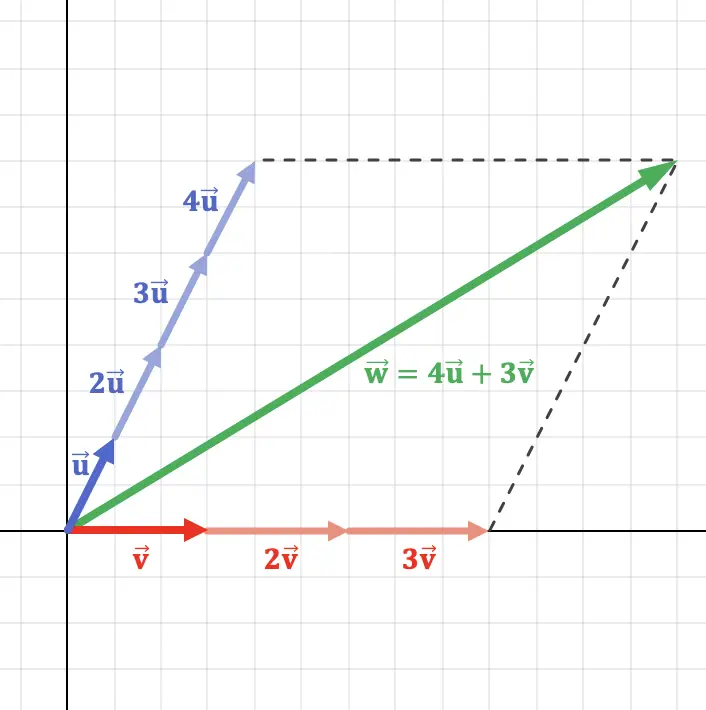
Seperti yang Anda lihat pada representasi grafis di atas, vektor
![]()
dapat diperoleh dari vektor
![]()
Dan
![]()
melakukan operasi vektor. Oleh karena itu, vektor
![]()
adalah kombinasi linier dari dua vektor lainnya.
Perlu ditekankan bahwa kombinasi linier ini bersifat unik , atau dengan kata lain hanya ada satu kombinasi linier yang layak untuk setiap vektor. Karena mengikuti contoh sebelumnya, jika kita mengalikannya
![]()
untuk 6, bukan 4, kita akan memperoleh vektor lain yang berbeda.
Selain itu, salah satu sifat dari kombinasi linier pada bidang (dalam R2) adalah bahwa suatu vektor dapat dikatakan sebagai kombinasi linier dari dua vektor lainnya jika keduanya mempunyai arah yang berbeda, yaitu jika keduanya tidak sejajar.
Selain itu, terkadang kita dapat mengidentifikasi dengan jelas bahwa dua vektor merupakan kombinasi linier. Untuk melakukan ini, komponen-komponennya cukup proporsional . Misalnya, koordinat dua vektor berikut adalah proporsional, sehingga vektor-vektor tersebut merupakan kombinasi linier:
![]()
![Rendered by QuickLaTeX.com \cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac41542948764e158ebe590c6b36e67_l3.png)
Terakhir, baik dalam ruang vektor dua dimensi (dalam R2) atau tiga dimensi (dalam R3), jika terdapat kombinasi linier dalam sekumpulan vektor, hal ini menunjukkan bahwa vektor-vektor tersebut saling bergantung secara linier . Sebaliknya, jika tidak ada kombinasi linier yang mungkin terjadi antar vektor, maka vektor-vektor tersebut bebas linier .
Jika konsep terakhir ini belum sepenuhnya jelas bagi Anda, kami sarankan untuk membaca penjelasan kami tentang vektor bergantung linier dan bebas , di sini Anda akan menemukan apa yang dimaksud dengan vektor bergantung atau bebas linier, contoh masing-masing jenis dan perbedaan di antara keduanya. . Konsep ini banyak digunakan dan bahkan banyak ditanyakan dalam ujian, jadi penting bagi Anda untuk memahaminya dengan baik.
Bagaimana menyatakan suatu vektor sebagai kombinasi linier dari vektor-vektor lainnya
Kita kemudian akan melihat bagaimana menyelesaikan masalah umum di mana kita diminta untuk menemukan kombinasi linier suatu vektor.
- Ekspresikan vektornya
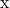
sebagai kombinasi linier dari
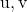
Dan
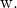
![]()
![]()
Sehingga vektornya
![]()
merupakan kombinasi linier dari vektor-vektor lainnya, maka persamaan berikut harus dipenuhi:
![]()
Dimana koefisiennya
![]()
Dan
![]()
Inilah hal-hal yang tidak diketahui yang harus kita temukan.
Oleh karena itu kami mengganti setiap vektor dengan koordinatnya:
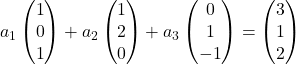
Kami mengalikan setiap vektor dengan koefisiennya:
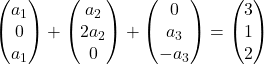
Kami menambahkan vektor:
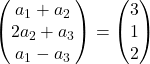
Setiap koordinat kiri harus sama dengan setiap koordinat kanan. Oleh karena itu kami memiliki 3 persamaan:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e5fe050102a285a325dcd81d07ef5d5_l3.png)
Yang tersisa hanyalah menyelesaikan sistem persamaan yang diperoleh. Untuk melakukannya, gunakan metode yang Anda sukai (metode substitusi, aturan Cramer, metode Gauss-Jordan, dll), dalam hal ini kita akan menggunakan metode Gauss:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8aa4e245614f286e0697797a18ba4465_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-41f1d9c941fe239bb40297b998eb6929_l3.png)
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-02a8a00406479f367627b682099e05c0_l3.png)
Oleh karena itu, sistem langkah-langkah yang diperoleh adalah:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-74ed1b18779582d6683ecaa1a9085e3d_l3.png)
Yang harus kita lakukan sekarang adalah mengklarifikasi hal-hal yang tidak diketahui dan menemukan nilainya. Jadi dari persamaan terakhir kita temukan
![]()
![]()
Dari persamaan kedua sistem, kita menghitung nilai
![]()
![]()
![]()
![]()
![]()
Dan akhirnya, dari persamaan pertama sistem langkah, kita menemukan hal yang tidak diketahui
![]()
![]()
Oleh karena itu, penyelesaian sistem persamaan linear adalah:
![]()
Jadi vektornya
![]()
Hal ini dapat dinyatakan dengan kombinasi linier berikut:
![]()
![]()
![]()
Oleh karena itu, secara efektif terdapat ketergantungan linier antar vektor. Di sisi lain, jika tidak ada solusi sistem persamaan yang diperoleh, ini berarti vektor
![]()
Ia bebas linier terhadap vektor-vektor lain dan, oleh karena itu, tidak ada kombinasi linier yang mungkin untuk memperoleh vektor tersebut dari vektor-vektor lain.
Latihan soal kombinasi linier vektor
Latihan 1
Di antara tiga vektor berikut, tunjukkan pasangan mana yang merupakan kombinasi linier satu sama lain. Selain itu, carilah hubungan kombinasi linier dari pasangan vektor tersebut.
![]()
Untuk mengetahui apakah suatu pasangan vektor merupakan kombinasi linier, kita harus melihat apakah koordinatnya sebanding.
Kita cek dulu vektornya
![]()
dengan vektornya
![]()
![]()
Kedua, kita periksa vektornya
![]()
dengan vektornya
![]()
![]()
Terakhir, kami menguji vektornya
![]()
dengan vektornya
![]()
![Rendered by QuickLaTeX.com \cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f818eb5ae0825dd43290331519599c21_l3.png)
Jadi satu-satunya pasangan vektor yang merupakan kombinasi linier adalah
![]()
Dan
![]()
Selanjutnya hubungan mereka adalah sebagai berikut:
![]()
Atau setara:
![]()
Meskipun pernyataan tersebut tidak mengharuskannya, satu-satunya vektor yang bergantung secara linear satu sama lain adalah
![]()
Dan
![]()
karena terdapat kombinasi linear diantara keduanya. Pasangan-pasangan lainnya bebas linier, karena tidak dapat digabungkan secara linier.
Latihan 2
Temukan hubungan linier antara vektor
![]()
dan himpunan vektor
![]()
Dan
![]()
![]()
![]()
Sehingga vektornya
![]()
merupakan kombinasi linier dari vektor-vektor lainnya, maka persamaan berikut harus dipenuhi:
![]()
Oleh karena itu kami mengganti setiap vektor dengan koordinatnya:
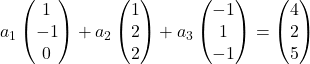
Kami mengalikan setiap vektor dengan konstanta:
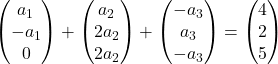
Kami menambahkan vektor:
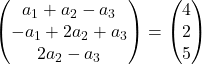
Oleh karena itu kami memperoleh sistem persamaan berikut:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ea3ca998fc7d9d9b2cf42d43a5bf0a4_l3.png)
Kami memecahkan sistem yang diperoleh dengan metode Gauss:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c808441bc71bd26e333ebe2169b738ca_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-941792a2de155bc284b14e34dc561418_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-7105de2fa579f40818bccc2df48961ab_l3.png)
Oleh karena itu, sistem langkah-langkah yang diperoleh adalah:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd5b2d564f66cd225c1a5987241ba14_l3.png)
Yang harus kita lakukan sekarang adalah mengklarifikasi hal-hal yang tidak diketahui dan menemukan nilainya. Jadi dari persamaan terakhir kita temukan
![]()
![]()
![]()
Dari persamaan kedua sistem, kita menghitung nilai
![]()
![]()
![]()
Dan akhirnya, dari persamaan pertama sistem langkah, kita menemukan hal yang tidak diketahui
![]()
![]()
![]()
![]()
Oleh karena itu, penyelesaian sistem persamaan linear adalah:
![]()
Jadi vektornya
![]()
Hal ini dapat dinyatakan dengan kombinasi linier berikut:
![]()
![]()
![]()
Latihan 3
Ekspresikan vektornya
![]()
sebagai kombinasi linier vektor
![]()
Dan
![]()
![]()
![]()
Kami mengusulkan persamaan kombinasi linier terhadap vektor
![]()
![]()
Oleh karena itu kami mengganti setiap vektor dengan komponen-komponennya:
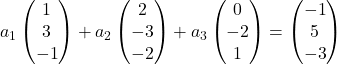
Kami mengalikan setiap vektor dengan masing-masing vektor yang tidak diketahui:
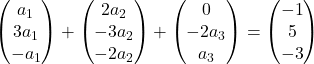
Kami melakukan penambahan vektor:
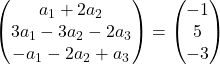
Oleh karena itu kami memperoleh sistem persamaan berikut:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-acdcf13a945bca16684be340d27e3523_l3.png)
Kami memecahkan sistem yang diperoleh dengan metode Gauss:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e49ae26fc68a865214bd9b6146b7aa99_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4c56b420242d0abe6f77b3ed1a60e54_l3.png)
Oleh karena itu, sistem langkah-langkah yang diperoleh adalah:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-03461ed9ebda463d2f0a1bb6894657be_l3.png)
Yang harus kita lakukan sekarang adalah mengklarifikasi hal-hal yang tidak diketahui dan menemukan nilainya. Jadi dari persamaan terakhir kita temukan
![]()
![]()
Dari persamaan kedua sistem, kita mencari nilai
![]()
![]()
![]()
![]()
![]()
![]()
Dan akhirnya, dari persamaan pertama sistem langkah, kita menyelesaikan hal yang tidak diketahui
![]()
![]()
Oleh karena itu, penyelesaian sistem persamaan linear adalah:
![]()
Jadi vektornya
![]()
dapat dinyatakan dengan menggabungkan vektor-vektor lainnya secara linear:
![]()
![]()
![]()
Latihan 4
Tentukan apakah vektornya
![]()
dapat dinyatakan sebagai kombinasi linier dari vektor-vektor
![]()
Dan
![]()
Dalam hal ini, temukan ekspresi yang menghubungkannya.
![]()
![]()
Sehingga vektornya
![]()
merupakan kombinasi linier dari vektor-vektor lainnya, maka persamaan berikut harus dipenuhi:
![]()
Oleh karena itu kami mengganti setiap vektor dengan koordinatnya:
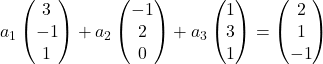
Kami mengalikan setiap vektor dengan koefisiennya:
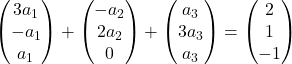
Kami menambahkan vektor:
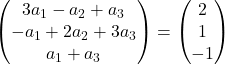
Oleh karena itu, ekspresi sebelumnya setara dengan sistem persamaan berikut:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f51b7e801b8314c51b983f1f24be15e4_l3.png)
Kami sekarang menyelesaikan sistem yang diperoleh dengan metode Gauss:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-031b14d5aca6a41d897ca575440b1197_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2caf1e1104b8b67e13d452bbd20d13b0_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4deec2426c0b9bb0b8e8a3d95155fd9_l3.png)
Oleh karena itu kami memperoleh sistem persamaan berikut:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e537d5c481ceedeaebf95334d72199ad_l3.png)
Namun, persamaan terakhir tidak akan pernah bisa dipenuhi, karena 0 tidak akan pernah sama dengan -30 berapa pun nilai yang diambil dari bilangan yang tidak diketahui. Oleh karena itu, sistem tidak memiliki solusi dan ini berarti tidak ada kombinasi linier untuk menghitung vektor
![]()