Cara mendiagonalisasi matriks

Di halaman ini Anda akan menemukan segala sesuatu tentang matriks yang dapat didiagonalisasi: apa itu matriks, kapan matriks tersebut dapat didiagonalisasi dan kapan tidak dapat didiagonalisasi, metode untuk mendiagonalisasi matriks, penerapan dan sifat-sifat matriks tertentu, dll. Dan Anda bahkan memiliki beberapa latihan yang diselesaikan selangkah demi selangkah sehingga Anda dapat berlatih dan memahami dengan sempurna bagaimana latihan tersebut didiagonalisasi. Terakhir, kita juga mempelajari cara melakukan diagonalisasi matriks dengan program komputer MATLAB, karena program ini sangat sering digunakan.

Apa yang dimaksud dengan matriks yang dapat didiagonalisasi?

Seperti yang akan kita lihat di bawah, mendiagonalisasi suatu matriks sangat berguna dalam bidang aljabar linier. Makanya banyak yang bertanya… apa itu diagonalisasi matriks? Nah, pengertian matriks yang dapat didiagonalisasi adalah:

Matriks yang dapat didiagonalisasi adalah matriks persegi yang dapat diubah menjadi matriks diagonal, yaitu matriks yang berisi angka nol kecuali pada diagonal utama. Diagonalisasi matriks dipecah sebagai berikut:

A = PDP^{-1}

Atau setara,

D = P^{-1}AP

Emas

A

adalah matriks yang akan didiagonalisasi,

P

adalah matriks yang kolomnya merupakan vektor eigen (atau vektor eigen).

A

,

P^{-1}

matriks inversnya dan

D

adalah matriks diagonal yang dibentuk oleh nilai eigen (atau nilai eigen) dari

A

.

Matriks

P

bertindak sebagai matriks perubahan basis, jadi sebenarnya dengan rumus ini kita mengubah basis menjadi matriks

A

, sehingga matriks tersebut menjadi matriks diagonal (

D

) di pangkalan baru.

Oleh karena itu, matriks

A

dan matriks

D

Mereka adalah matriks yang serupa. Dan jelas,

P

Ini adalah matriks reguler atau non-degenerasi.

Kapankah suatu matriks dapat didiagonalisasi?

Tidak semua matriks dapat didiagonalisasi; hanya matriks yang memenuhi karakteristik tertentu yang dapat didiagonalisasi. Anda dapat mengetahui apakah suatu matriks dapat didiagonalisasi dengan berbagai cara:

  • Suatu matriks persegi berorde n dapat didiagonalisasi jika mempunyai n vektor eigen (atau vektor eigen) yang bebas linier , atau dengan kata lain, jika vektor-vektor tersebut membentuk basis. Hal ini karena matriks

    P

    , yang digunakan untuk mendiagonalisasi suatu matriks, dibentuk oleh vektor eigen matriks tersebut. Untuk mengetahui apakah vektor eigennya LI, cukup determinan matriksnya

    P

    berbeda dengan 0 yang berarti matriks mempunyai rank maksimum.

\text{si} \quad \text{det}(P)\neq 0 \ \longrightarrow \ \text{matriz diagonalizable}

  • Sifat nilai eigen dan vektor eigen adalah bahwa vektor eigen dari nilai eigen yang berbeda adalah bebas linier. Oleh karena itu, jika semua nilai eigen matriks adalah unik, maka matriks tersebut dapat didiagonalisasi.
  • Cara lain untuk menentukan apakah suatu matriks dapat ditampung dalam matriks diagonal adalah dengan menggunakan multiplisitas aljabar dan geometri. Multiplisitas aljabar adalah berapa kali suatu nilai eigen (atau nilai eigen) diulang, dan multiplisitas geometri adalah dimensi inti (atau inti) matriks dengan mengurangkan nilai eigen pada diagonal utamanya. Jadi, jika untuk setiap nilai eigen multiplisitas aljabar sama dengan multiplisitas geometri , matriks tersebut dapat didiagonalisasi.

\alpha_\lambda = \text{multiplicidad algebraica} = \text{multiplicidad del valor propio}

m_\lambda = \text{multiplicidad geom\'etrica} = \text{dim } Ker(A-\lambda I) = n -rg(A-\lambda I)

\alpha_\lambda \geq m_\lambda \geq 1

\text{si} \quad \alpha_\lambda = m_\lambda \quad \forall \lambda \ \longrightarrow \ \text{matriz diagonalizable}

  • Terakhir, ada teorema, teorema spektral, yang menjamin diagonalisasi matriks simetris dengan bilangan real. Dengan kata lain, setiap matriks real dan simetris dapat didiagonalisasi .

Cara mendiagonalisasi matriks

Prosedur untuk mendiagonalisasi suatu matriks didasarkan pada pencarian nilai eigen (atau nilai eigen) dan vektor eigen (atau vektor eigen) suatu matriks. Inilah mengapa penting bagi Anda untuk menguasai cara menghitung nilai eigen (atau nilai eigen) dan vektor eigen (atau vektor eigen) dari matriks apa pun . Anda dapat mengingat cara melakukannya dengan mengeklik tautannya, di mana kami menjelaskan langkah demi langkah cara menemukannya dan beberapa trik yang membuat penghitungan menjadi lebih mudah. Selain itu, Anda juga akan menemukan latihan terpecahkan untuk dipraktikkan.

Dengan metode berikut, Anda dapat mendiagonalisasi matriks dengan dimensi apa pun: 2×2, 3×3, 4×4, dst. Langkah-langkah yang harus diikuti untuk mendiagonalisasi suatu matriks adalah:

  1. Dapatkan nilai eigen (atau nilai eigen) dari matriks.
  2. Hitung vektor eigen yang terkait dengan setiap nilai eigen.
  3. Bangun matriksnya

    P

    , yang kolomnya merupakan vektor eigen dari matriks yang akan didiagonalisasi.

  4. Periksa apakah matriks dapat didiagonalisasi (harus memenuhi salah satu syarat yang dijelaskan pada bagian sebelumnya).
  5. Buatlah matriks diagonal

    D

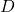
    , yang elemennya semuanya 0 kecuali yang ada pada diagonal utama, yang merupakan nilai eigen yang ditemukan pada langkah 1.

Peringatan: Vektor eigen dari matriks

P

dapat ditempatkan dalam urutan apa pun, kecuali nilai eigen matriks diagonal

D

Mereka harus ditempatkan dalam urutan yang sama. Misalnya nilai eigen pertama dari matriks diagonal

D

haruslah vektor yang sesuai dengan vektor eigen kolom pertama matriks

P

.

Di bawah ini beberapa latihan diagonalisasi matriks langkah demi langkah yang dapat Anda praktikkan.

Latihan diagonalisasi matriks diselesaikan

Latihan 1

Diagonalisasikan matriks persegi berdimensi 2×2 berikut:

\displaystyle A= \begin{pmatrix}2&2\\[1.1ex] 1&3\end{pmatrix}

Pertama-tama kita harus menentukan nilai eigen matriks A. Oleh karena itu, kita menghitung persamaan karakteristik dengan menyelesaikan determinan berikut:

\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2- \lambda &2\\[1.1ex] 1&3-\lambda \end{vmatrix} = \lambda^2-5\lambda +4

Sekarang mari kita hitung akar-akar polinomial karakteristik:

\displaystyle \lambda^2-5\lambda +4=0 \ \longrightarrow \ \begin{cases} \lambda = 4 \\[2ex] \lambda = 1 \end{cases}

Setelah nilai eigen diperoleh, kami menghitung vektor eigen yang terkait dengan masing-masing nilai eigen. Pertama, vektor eigen yang sesuai dengan nilai eigen 1:

\displaystyle (A-I)v=0

\displaystyle \begin{pmatrix}1&2\\[1.1ex] 1&2\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}

\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] x+2y = 0\end{array}\right\} \longrightarrow \ x=-2y

\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] 1 \end{pmatrix}

Dan kemudian kita menghitung vektor eigen yang terkait dengan nilai eigen 4:

\displaystyle (A-4I)v=0

\displaystyle \begin{pmatrix}-2&2\\[1.1ex] 1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}

\displaystyle \left.\begin{array}{l} -2x+2y = 0 \\[2ex] x-y = 0\end{array}\right\} \longrightarrow \ y=x

\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 1 \end{pmatrix}

Kami membangun matriks

P

, dibentuk oleh vektor eigen matriks:

\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix}

Karena semua nilai eigennya berbeda, maka matriks A dapat didiagonalisasi. Jadi matriks diagonal yang bersesuaian adalah matriks yang mempunyai nilai eigen pada diagonal utama:

\displaystyle D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}

Ingatlah bahwa nilai eigen harus ditempatkan dalam urutan yang sama dengan penempatan vektor eigen dalam matriks

P

.

Kesimpulannya, matriks perubahan basis dan matriks yang didiagonalisasi adalah:

\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}

Latihan 2

Diagonalisasikan matriks persegi berorde 2 berikut:

\displaystyle A= \begin{pmatrix}3&4\\[1.1ex] -1&-2\end{pmatrix}

Pertama-tama kita harus menentukan nilai eigen matriks A. Oleh karena itu, kita menghitung persamaan karakteristik dengan menyelesaikan determinan berikut:

\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3- \lambda &4\\[1.1ex] -1&-2-\lambda \end{vmatrix} = \lambda^2-\lambda -2

Sekarang mari kita hitung akar-akar polinomial karakteristik:

\displaystyle \lambda^2-\lambda -2=0 \ \longrightarrow \ \begin{cases} \lambda = -1 \\[2ex] \lambda = 2 \end{cases}

Setelah nilai eigen diperoleh, kami menghitung vektor eigen yang terkait dengan masing-masing nilai eigen. Pertama, vektor eigen yang sesuai dengan nilai eigen -1:

\displaystyle (A+I)v=0

\displaystyle \begin{pmatrix}4&4\\[1.1ex] -1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}

\displaystyle \left.\begin{array}{l} 4x+4y = 0 \\[2ex] -x-y = 0\end{array}\right\} \longrightarrow \ x=-y

\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 1 \end{pmatrix}

Dan kemudian kita menghitung vektor eigen yang terkait dengan nilai eigen 2:

\displaystyle (A-2I)v=0

\displaystyle \begin{pmatrix}1&4\\[1.1ex] -1&-4\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}

\displaystyle \left.\begin{array}{l} x+4y = 0 \\[2ex] -x-4y = 0\end{array}\right\} \longrightarrow \ x=-4y

\displaystyle v = \begin{pmatrix}-4 \\[1.1ex] 1 \end{pmatrix}

Kami membangun matriks

P

, dibentuk oleh vektor eigen matriks:

\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1 \end{pmatrix}

Karena semua nilai eigen berbeda satu sama lain, matriks A dapat didiagonalisasi. Jadi matriks diagonal yang bersesuaian adalah matriks yang memuat nilai eigen pada diagonal utama:

\displaystyle D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}

Ingatlah bahwa nilai eigen harus ditempatkan dalam urutan yang sama dengan penempatan vektor eigen dalam matriks

P

.

Kesimpulannya, matriks perubahan basis dan matriks yang didiagonalisasi adalah:

\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1\end{pmatrix} \qquad D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}

Latihan 3

Diagonalisasikan matriks persegi berdimensi 3×3 berikut:

\displaystyle A= \begin{pmatrix}2&0&2\\[1.1ex] -1&2&1\\[1.1ex] 0&1&4\end{pmatrix}

Langkah pertama adalah mencari nilai eigen matriks A. Oleh karena itu, kita menghitung persamaan karakteristik dengan menyelesaikan determinan matriks berikut:

\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&0&2\\[1.1ex] -1&2-\lambda&1\\[1.1ex] 0&1&4-\lambda \end{vmatrix} = -\lambda^3+8\lambda^2-19\lambda+12

Sekarang kita harus menghitung akar-akar polinomial karakteristik. Karena merupakan polinomial derajat ketiga, kami menerapkan aturan Ruffini:

\displaystyle \begin{array}{r|rrrr} & -1&8&-19& 12 \\[2ex] 1 & & -1&7&-12 \\ \hline &-1\vphantom{\Bigl)}&7&-12&0 \end{array}

Dan kemudian kita menemukan akar polinomial yang diperoleh:

\displaystyle -\lambda^2+7\lambda -12=0 \ \longrightarrow \ \begin{cases} \lambda = 3 \\[2ex] \lambda = 4 \end{cases}

Jadi nilai eigen matriksnya adalah:

\lambda=1 \qquad \lambda =3 \qquad \lambda = 4

Setelah nilai eigen ditemukan, kami menghitung vektor eigen yang terkait dengan masing-masing nilai tersebut. Pertama, vektor eigen yang sesuai dengan nilai eigen 1:

\displaystyle (A-I)v=0

\displaystyle \begin{pmatrix}1&0&2\\[1.1ex] -1&1&1\\[1.1ex] 0&1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} x+2z = 0 \\[2ex] -x+y+z = 0\\[2ex] y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=-2z \\[2ex] y = -3z \end{array}

\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] -3 \\[1.1ex] 1\end{pmatrix}

Kemudian kita menghitung vektor eigen yang terkait dengan nilai eigen 3:

\displaystyle (A-3I)v=0

\displaystyle \begin{pmatrix}-1&0&2\\[1.1ex] -1&-1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} -x+2z = 0 \\[2ex] -x-y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=2z \\[2ex] y = -z \end{array}

\displaystyle v = \begin{pmatrix}2 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}

Dan terakhir, kami menghitung vektor eigen yang terkait dengan nilai eigen 4:

\displaystyle (A-4I)v=0

\displaystyle \begin{pmatrix}-2&0&2\\[1.1ex] -1&-2&1\\[1.1ex] 0&1&0\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} -2x+2z = 0 \\[2ex] -x-2y+z = 0\\[2ex] y = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=z \\[2ex] y = 0 \end{array}

\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 1\end{pmatrix}

Kami membangun matriks

P

, dibentuk oleh vektor eigen matriks:

\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1 \end{pmatrix}

Karena semua nilai eigen berbeda satu sama lain, matriks A dapat didiagonalisasi. Jadi matriks diagonal yang bersesuaian adalah matriks yang mempunyai nilai eigen pada diagonal utamanya:

\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}

Ingatlah bahwa nilai eigen harus ditempatkan dalam urutan yang sama dengan penempatan vektor eigen dalam matriks

P

.

Singkatnya, matriks perubahan basis dan matriks yang didiagonalisasi adalah:

\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1\end{pmatrix} \qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}

Latihan 4

Diagonalisasikan, jika memungkinkan, matriks persegi berorde 3 berikut:

\displaystyle A= \begin{pmatrix}-1&3&1\\[1.1ex] 0&2&0\\[1.1ex] 3&-1&1\end{pmatrix}

Langkah pertama adalah mencari nilai eigen matriks A. Oleh karena itu, kita menghitung persamaan karakteristik dengan menyelesaikan determinan matriks berikut:

\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}-1-\lambda&3&1\\[1.1ex] 0&2-\lambda&0\\[1.1ex] 3&-1&1-\lambda \end{vmatrix} = -\lambda^3+2\lambda^2+4\lambda-8

Sekarang kita harus menghitung akar-akar polinomial minimum. Karena merupakan polinomial derajat ketiga, kita menerapkan aturan Ruffini untuk memfaktorkannya:

\displaystyle \begin{array}{r|rrrr} & -1&2&\phantom{-}4& -8 \\[2ex] 2 & & -2&0&8 \\ \hline &-1\vphantom{\Bigl)}&0&4&0 \end{array}

Dan kemudian kita menemukan akar polinomial yang diperoleh:

\displaystyle -\lambda^2+4=0 \ \longrightarrow \ \begin{cases} \lambda = +2 \\[2ex] \lambda = -2 \end{cases}

Jadi nilai eigen matriksnya adalah:

\lambda=2 \qquad \lambda =2 \qquad \lambda = -2

Nilai eigen dari -2 adalah multiplisitas aljabar sederhana, sebaliknya nilai eigen dari 2 adalah multiplisitas ganda.

Setelah nilai eigen ditemukan, kami menghitung vektor eigen yang terkait dengan masing-masing nilai tersebut. Pertama, vektor eigen yang sesuai dengan nilai eigen -2:

\displaystyle (A+2I)v=0

\displaystyle \begin{pmatrix}1&3&1\\[1.1ex] 0&4&0\\[1.1ex] 3&-1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} x+3y+z = 0 \\[2ex] 4y = 0\\[2ex] 3x-y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] x = -z \end{array}

\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] -1\end{pmatrix}

Sekarang mari kita hitung vektor eigen yang terkait dengan nilai eigen 2.

\displaystyle (A-2I)v=0

\displaystyle \begin{pmatrix}-3&3&1\\[1.1ex] 0&0&0\\[1.1ex] 3&-1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} -3x+3y+z = 0 \\[2ex] 0= 0\\[2ex] 3x-y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] z=3x \end{array}

\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 3\end{pmatrix}

Karena nilai eigen 2 diulang dua kali, kita perlu menghitung vektor eigen lain yang memenuhi persamaan subruang (atau ruang eigen):

\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] -3\end{pmatrix}

Kami membangun matriks

P

, dibentuk oleh tiga vektor eigen matriks:

\displaystyle P = \begin{pmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{pmatrix}

Namun ketiga vektor tersebut tidak bebas linier, karena jelas kedua vektor eigen dengan nilai eigen 2 merupakan kombinasi linier satu sama lain. Hal ini juga dapat ditunjukkan karena determinan dari matriks

P

sama dengan 0 (memiliki garis penuh nol):

\displaystyle \text{det}(P) = \begin{vmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{vmatrix}=0

Oleh karena itu, karena vektor eigen bergantung linier, matriks A tidak dapat didiagonalisasi .

Latihan 5

Jika memungkinkan, diagonalkan matriks persegi berikut berukuran 3×3:

\displaystyle A= \begin{pmatrix}3&0&0\\[1.1ex] 0&2&1\\[1.1ex] 0&1&2\end{pmatrix}

Langkah pertama adalah mencari nilai eigen matriks A. Oleh karena itu, kita menghitung persamaan karakteristik dengan menyelesaikan determinan matriks berikut:

\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}

Karena baris pertama seluruhnya terdiri dari nol kecuali 3, kita akan memanfaatkan ini untuk menyelesaikan determinan matriks dengan kofaktor (atau adjoin):

\displaystyle \begin{aligned} \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}& = (3-\lambda)\cdot \begin{vmatrix} 2-\lambda&1\\[1.1ex]1&2-\lambda \end{vmatrix} \\[3ex] & = (3-\lambda)[\lambda^2 -4\lambda +3] \end{aligned}

Sekarang kita perlu menghitung akar-akar polinomial karakteristik. Sebaiknya jangan mengalikan tanda kurung karena Anda akan mendapatkan polinomial derajat ketiga. Sebaliknya, jika kedua faktor diselesaikan secara terpisah, maka akan lebih mudah untuk mendapatkan nilai eigennya:

\displaystyle (3-\lambda)[\lambda^2 -4\lambda +3]=0 \ \longrightarrow \ \begin{cases} 3-\lambda=0 \ \longrightarrow \ \lambda = 3 \\[2ex] \lambda^2 -4\lambda +3=0 \ \longrightarrow \begin{cases}\lambda = 1 \\[2ex] \lambda = 3 \end{cases} \end{cases}

Jadi nilai eigen matriksnya adalah:

\lambda=1 \qquad \lambda =3 \qquad \lambda = 3

Setelah nilai eigen ditemukan, kami menghitung vektor eigen yang terkait dengan masing-masing nilai tersebut. Pertama, vektor eigen yang sesuai dengan nilai eigen 1:

\displaystyle (A-I)v=0

\displaystyle \begin{pmatrix}2&0&0\\[1.1ex] 0&1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} 2x = 0 \\[2ex] y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=0 \\[2ex] y = -z \end{array}

\displaystyle v = \begin{pmatrix}0 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}

Kemudian kita menghitung vektor eigen yang terkait dengan nilai eigen 3:

\displaystyle (A-3I)v=0

\displaystyle \begin{pmatrix}0&0&0\\[1.1ex] 0&-1&1\\[1.1ex] 0&1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} 0 = 0 \\[2ex] -y+z = 0\\[2ex] y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=z \end{array}

\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 1 \\[1.1ex] 1\end{pmatrix}

Karena nilai eigen 3 diulang dua kali, kita perlu menghitung vektor eigen lain yang memenuhi persamaan ruang eigen:

\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

Kami membangun matriks

P

, dibentuk oleh vektor eigen matriks:

\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}

Berbeda dengan latihan 4, dalam kasus ini kita mampu membentuk 3 vektor bebas linier meskipun multiplisitas aljabar dari nilai eigen 3 adalah dua kali lipat. Hal ini dapat dibuktikan dengan melihat determinan matriks tersebut

P

memberikan hasil yang berbeda dari 0:

\displaystyle \text{det}(P) = \begin{vmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{vmatrix} =-2 \neq 0

Dengan demikian kita dapat melakukan dekomposisi diagonal dari matriks A. Dan matriks diagonal yang bersesuaian adalah matriks yang memiliki nilai eigen pada diagonal utama:

\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}

Ingatlah bahwa nilai eigen harus ditempatkan dalam urutan yang sama dengan penempatan vektor eigen dalam matriks

P

.

Singkatnya, matriks perubahan basis yang diperlukan untuk mendiagonalisasi matriks dan bentuk diagonalnya adalah:

\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}\qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}

Latihan 6

Jika memungkinkan, lakukan diagonalisasi matriks berdimensi 4×4 berikut:

\displaystyle A=\begin{pmatrix}2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}

Langkah pertama adalah mencari nilai eigen matriks A. Oleh karena itu, kita menghitung persamaan karakteristik dengan menyelesaikan determinan matriks berikut:

\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}

Dalam hal ini, kolom terakhir determinan hanya terdiri dari nol kecuali satu elemen, oleh karena itu kita akan memanfaatkan ini untuk menghitung determinan berdasarkan kofaktor melalui kolom ini:

\displaystyle \begin{aligned} \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}& = (5-\lambda)\cdot \begin{vmatrix}2-\lambda&1&2\\[1.1ex] 1&-3-\lambda&1\\[1.1ex] 0&-1&-\lambda\end{vmatrix}\\[3ex] & = (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda] \end{aligned}

Sekarang kita harus menghitung akar-akar polinomial karakteristik. Sebaiknya jangan mengerjakan perkalian tanda kurung karena Anda akan mendapatkan polinomial derajat keempat. Namun, jika kedua faktor tersebut diselesaikan secara terpisah, akan lebih mudah untuk menghitung nilai eigennya:

\displaystyle (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda]=0 \ \longrightarrow \ \begin{cases} 5-\lambda=0 \ \longrightarrow \ \lambda = 5 \\[2ex] -\lambda^3 -\lambda^2 +6\lambda =0 \ \longrightarrow \ \lambda(-\lambda^2 -\lambda +6) =0 \end{cases}

\displaystyle \lambda(-\lambda^2 -\lambda +6)=0 \ \longrightarrow \ \begin{cases} \lambda=0 \\[2ex] -\lambda^2 -\lambda +6=0 \ \longrightarrow \ \begin{cases} \lambda=2 \\[2ex] \lambda = -3 \end{cases}\end{cases}

Jadi nilai eigen matriksnya adalah:

\lambda=0 \qquad \lambda =-3 \qquad \lambda = 2\qquad \lambda = 5

Setelah semua nilai eigen ditemukan, kita beralih ke vektor eigen. Kami menghitung vektor eigen yang terkait dengan nilai eigen 0:

\displaystyle (A-0I)v=0

\displaystyle \begin{pmatrix} 2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} 2w+x+2y = 0 \\[2ex] w-3x+y = 0\\[2ex] -x=0 \\[2ex] 5z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=0 \\[2ex] z=0 \\[2ex]w=-y \end{array}

\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}

Kami menghitung vektor eigen yang terkait dengan nilai eigen -3:

\displaystyle (A+3I)v=0

\displaystyle \begin{pmatrix} 5&1&2&0\\[1.1ex] 1&0&1&0\\[1.1ex] 0&-1&3&0\\[1.1ex] 0&0&0&8\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} 5w+x+2y = 0 \\[2ex] w+y = 0\\[2ex] -x+3y=0 \\[2ex] 8z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=-y \\[2ex]x=3y \\[2ex] z=0 \end{array}

\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 3 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}

Kami menghitung vektor eigen yang terkait dengan nilai eigen 2:

\displaystyle (A-2I)v=0

\displaystyle \begin{pmatrix} 0&1&2&0\\[1.1ex] 1&-5&1&0\\[1.1ex] 0&-1&-2&0\\[1.1ex] 0&0&0&3\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] w-5x+y = 0\\[2ex] -x-2y=0 \\[2ex] 3z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=-2y \\[2ex] w=-11y \\[2ex] z=0 \end{array}

\displaystyle v = \begin{pmatrix}-11 \\[1.1ex] -2 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}

Kami menghitung vektor eigen yang terkait dengan nilai eigen 5:

\displaystyle (A-5I)v=0

\displaystyle \begin{pmatrix} -3&1&2&0\\[1.1ex] 1&-8&1&0\\[1.1ex] 0&-1&-5&0\\[1.1ex] 0&0&0&0\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}

\displaystyle \left.\begin{array}{l} -3w+x+2y = 0 \\[2ex] w-8x+y = 0\\[2ex] -x-5y=0 \\[2ex] 0=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=x=y=0 \end{array}

\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0 \\[1.1ex]1 \end{pmatrix}

Kami membuat matriks

P

, terdiri dari vektor eigen matriks:

\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix}

Karena semua nilai eigen berbeda satu sama lain, matriks A dapat didiagonalisasi. Jadi matriks diagonal yang bersesuaian adalah matriks yang mempunyai nilai eigen pada diagonal utama:

\displaystyle D= \begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}

Ingatlah bahwa nilai eigen harus ditempatkan dalam urutan yang sama dengan penempatan vektor eigen dalam matriks

P

.

Ringkasnya, perubahan matriks dasar yang diperlukan untuk mendiagonalisasi matriks A dan matriks dalam bentuk diagonal adalah:

\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix} \qquad D=\begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}

Penerapan matriks yang dapat didiagonalisasi

Jika Anda sudah sampai sejauh ini, Anda mungkin bertanya-tanya: untuk apa matriks yang dapat didiagonalisasi?

Nah, matriks yang dapat didiagonalisasi sangat berguna dan banyak digunakan dalam matematika. Alasannya adalah matriks diagonal praktis penuh dengan angka nol sehingga membuat perhitungan menjadi lebih mudah.

Contoh nyata dari hal ini adalah pangkat matriks yang dapat didiagonalisasi, karena hasilnya disederhanakan dengan rumus berikut:

\displaystyle A^k=PD^kP^{-1}

Kesetaraan ini dapat dengan mudah dibuktikan dengan induksi. Oleh karena itu cukup untuk menaikkan matriks

D

kepada peserta pameran. Dan karena ini adalah matriks diagonal, operasinya dikurangi menjadi menaikkan setiap suku diagonal utama menjadi eksponen:

\displaystyle D^k = diag(\lambda_1^k,\lambda_2^k, \ldots , \lambda_n^k)

Contoh pangkat matriks yang dapat didiagonalisasi

Untuk lebih memahaminya, kita akan menghitung pangkat matriks yang dapat didiagonalisasi sebagai contoh:

\displaystyle A= \begin{pmatrix}2&0\\[1.1ex] 3&1\end{pmatrix}

Matriks Perubahan Dasar

P

, dibentuk oleh vektor eigennya, dan matriks yang didiagonalisasi

D

, terdiri dari nilai-nilainya sendiri, adalah:

\displaystyle P = \begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}

Jadi, sebagai contoh, matriks A yang dipangkatkan menjadi 7 ekuivalen dengan:

\displaystyle A^7=PD^7P^{-1}

\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\left.\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\right.^{-1}

Sekarang kita membalikkan matriksnya

P:

\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}

Kami memecahkan kekuatan matriks

D:

\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1^7&0\\[1.1ex] 0&2^7\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}

\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&128\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}

Dan terakhir, kita melakukan perkalian matriks:

\displaystyle \bm{A^7=}\begin{pmatrix}\bm{128}&\bm{0}\\[1.1ex] \bm{381}&\bm{1}\end{pmatrix}

Seperti yang Anda lihat, menghitung pangkat dengan matriks diagonal lebih mudah daripada mengalikan matriks yang sama tujuh kali berturut-turut. Lalu bayangkan dengan nilai eksponen yang jauh lebih besar.

Sifat-sifat matriks yang dapat didiagonalisasi

Ciri-ciri matriks jenis ini adalah:

  • Jika matriks

    A

    dapat didiagonalisasi, kekuatan apa pun

    A

    .

  • Hampir semua matriks dapat didiagonalisasi pada lingkungan yang kompleks

    \mathbb{C}

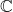
    . Meskipun di bawah ini Anda memiliki pengecualian yang tidak pernah dapat didiagonalisasi.

  • Jika matriks

    P

    adalah matriks ortogonal, maka kita katakan matriks tersebut

    A

    dapat didiagonalisasi secara ortogonal dan, oleh karena itu, persamaannya dapat ditulis ulang:

\displaystyle A=PDP^t

  • Suatu matriks dapat didiagonalisasi oleh matriks kesatuan jika dan hanya jika matriks tersebut merupakan matriks normal.
  • Diberikan dua matriks yang dapat didiagonalisasi, matriks-matriks tersebut dapat diubah jika dan hanya jika matriks-matriks tersebut dapat didiagonalisasi secara bersamaan, yaitu jika matriks-matriks tersebut memiliki basis vektor eigen (atau vektor eigen) ortonormal yang sama.
  • Jika suatu endomorfisme dapat didiagonalisasi, kita katakan bahwa endomorfisme tersebut dapat didiagonalisasi karena kesamaan . Namun, tidak semua endomorfisme dapat didiagonalisasi, atau dengan kata lain, diagonalisasi suatu endomorfisme tidak terjamin.

Diagonalisasi Serentak

Suatu himpunan matriks dikatakan dapat didiagonalisasi secara serentak jika terdapat matriks yang dapat dibalik yang menjadi dasar untuk mendiagonalisasi matriks mana pun dalam himpunan tersebut. Dengan kata lain, jika dua matriks didiagonalisasi berdasarkan vektor eigen yang sama, berarti matriks-matriks tersebut dapat didiagonalisasi secara bersamaan.

Selain itu, seperti yang telah kami komentari dalam sifat-sifat diagonalisasi matriks, jika dua matriks mampu melakukan diagonalisasi secara bersamaan, keduanya harus saling berpindah-pindah.

Misalnya, dua matriks berikut dapat diubah, sehingga keduanya didiagonalisasi berdasarkan vektor eigen atau vektor eigen yang sama.

\displaystyle A=\begin{pmatrix}2&0 \\[1.1ex] 1&-1 \end{pmatrix} \qquad B=\begin{pmatrix}3&0\\[1.1ex] 1&0 \end{pmatrix}

Sekalipun keduanya memiliki vektor eigen yang sama, bukan berarti keduanya mempunyai nilai eigen yang sama. Faktanya, meskipun matriks A dan B di atas memiliki vektor eigen yang sama, namun nilai eigennya berbeda.

Matriks yang tidak dapat didiagonalisasi

Meskipun sebagian besar matriks dapat didiagonalisasi dalam lingkungan bilangan kompleks, beberapa matriks tidak pernah dapat didiagonalisasi.

Fakta ini terjadi ketika multiplisitas aljabar suatu nilai eigen (atau nilai eigen) tidak sesuai dengan multiplisitas geometri.

Misalnya, matriks berikut tidak dapat didiagonalisasi dengan cara apa pun, melainkan “dapat didiagonalisasi”:

\displaystyle \begin{pmatrix}0&1 \\[1.1ex] 0&0 \end{pmatrix}

Selain itu, ada matriks yang tidak mampu melakukan diagonalisasi dalam lingkungan bilangan real, tetapi matriks tersebut melakukan diagonalisasi ketika bekerja dengan bilangan kompleks, seperti matriks ini:

\displaystyle \begin{pmatrix}0&1 \\[1.1ex] -1&0 \end{pmatrix}

Terakhir, ada beberapa prosedur diagonalisasi blok matriks yang tidak sepenuhnya dapat didiagonalisasi, namun sedikit lebih rumit. Metode yang paling terkenal adalah diagonalisasi dengan bentuk kanonik Jordan .

Mendiagonalisasi matriks dengan MATLAB

Program komputer sangat berguna dalam mendiagonalisasi matriks, terutama jika matriksnya sangat besar. Dan software yang paling terkenal tentunya MATLAB , jadi selanjutnya kita akan melihat cara memfaktorkan matriks secara diagonal menggunakan program ini.

Instruksi yang digunakan untuk mendiagonalisasi matriks dengan MATLAB adalah:

\displaystyle \text{[P, D] = eig(A)}

Emas

A

adalah matriks yang akan didiagonalisasi dan

P

Dan

D

adalah matriks yang dikembalikan oleh program:

P

adalah matriks yang dibentuk oleh vektor eigen dan

D

adalah matriks berbentuk diagonal yang suku diagonal utamanya adalah nilai eigennya.

Oleh karena itu, Anda hanya perlu memasukkan kode ini ke dalam program.

Sebaliknya, jika Anda hanya ingin mengetahui nilai eigen saja, Anda dapat menggunakan pernyataan berikut:

\displaystyle e= eig(A)}

Emas

e

adalah vektor kolom yang dikembalikan MATLAB dengan nilai eigen matriks

A

.

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top