Di halaman ini, kami menjelaskan cara melakukan penguraian (atau ekspresi) polinomial suatu bilangan. Di sini Anda dapat melihat contoh dekomposisi polinomial dan, sebagai tambahan, Anda akan menemukan latihan langkah demi langkah yang dapat diselesaikan untuk dipraktikkan.
Apa yang dimaksud dengan penguraian polinomial suatu bilangan?
Dalam matematika, penguraian polinomial suatu bilangan terdiri dari menyatakan bilangan tersebut dalam suatu penjumlahan, sehingga setiap suku dari jumlah tersebut adalah hasil kali setiap digit bilangan tersebut dengan pangkat basis 10.
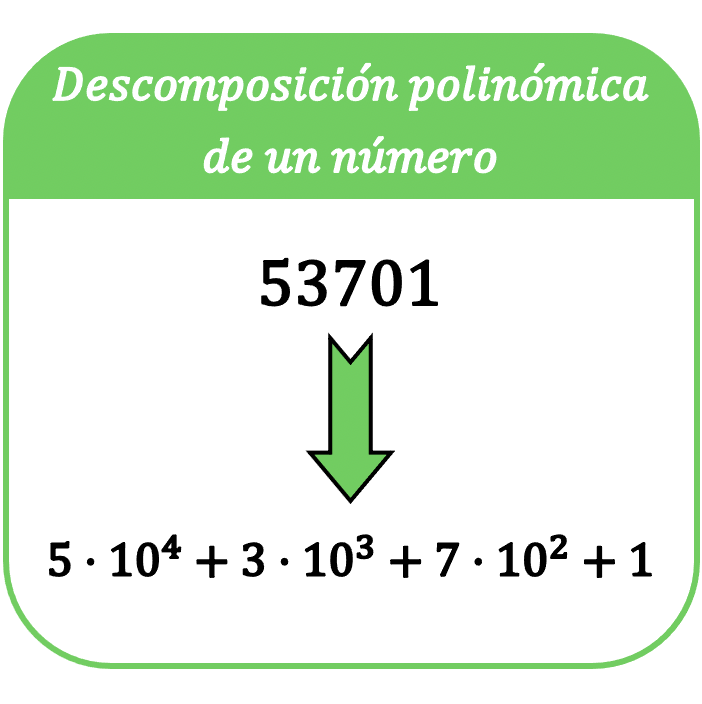
Istilah penguraian polinomial suatu bilangan disebut juga dengan ekspresi polinomial suatu bilangan .
Cara melakukan dekomposisi polinomial
Untuk melakukan penguraian polinomial suatu bilangan, Anda harus mengalikan setiap digit bilangan tersebut dengan 10 yang dipangkatkan ke banyaknya digit di sebelah kanan .
Misalnya, jika kita ingin menghitung penguraian polinomial bilangan berikut:
![]()
Dalam hal ini angka 8 menempati posisi kelima sehingga mempunyai 4 angka di sebelah kanannya. Oleh karena itu, kita harus mengalikan delapan dengan sepuluh pangkat empat:
![]()
Jadi, untuk menguraikan bilangan 86293 secara polinomial, Anda harus melakukan hal yang sama dengan semua digit bilangan tersebut, dan menyatakan semua perkaliannya dalam bentuk penjumlahan:
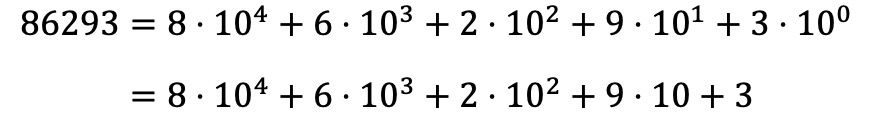
Perhatikan bahwa pangkat 10 0 hilang karena, berdasarkan sifat pangkat, bilangan apa pun yang dipangkatkan 0 sama dengan 1, jadi 10 0 =1.
Di sisi lain, Anda juga dapat mencari dekomposisi polinomial suatu bilangan dari dekomposisi perkaliannya:
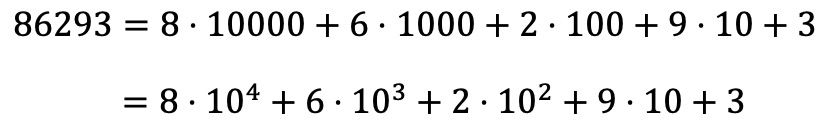
Contoh penguraian bilangan polinomial
Setelah kita melihat bagaimana penguraian polinomial suatu bilangan dilakukan, kita akan melihat berbagai contoh jenis operasi ini untuk memahami konsepnya sepenuhnya.
- Dekomposisi polinomial 3641:
![]()
- Dekomposisi polinomial 56912:
![]()
- Dekomposisi polinomial 27084:
![Rendered by QuickLaTeX.com \begin{aligned} 27084 &= 2\cdot 10^4 +7\cdot 10^3 +0\cdot 10^2 + 8\cdot 10 + 4 \\[2ex] & = 2\cdot 10^4 +7\cdot 10^3 + 8\cdot 10 + 4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f72230330ff9c9150dc9ab19a89a42d8_l3.png)
Dalam contoh terakhir ini, kita dapat menyederhanakan perkalian ketiga karena bilangan apa pun yang dikalikan dengan nol akan hilang.
Dekomposisi polinomial dari bilangan desimal
Kita baru saja melihat cara melakukan penguraian polinomial bilangan asli. Tapi… bagaimana cara menguraikan bilangan desimal secara polinomial?
Nah, penguraian polinomial dengan bilangan desimal dilakukan dengan cara yang sama seperti bilangan bulat, tetapi sebagai tambahan, kita menjumlahkan hasil kali setiap angka desimal dikalikan pangkat basis 10 yang eksponennya adalah posisi desimal yang ditempati oleh angka tersebut dengan negatif tanda.
Jika dijelaskan dengan kata-kata, hal ini mungkin tampak sangat rumit, tetapi Anda akan melihat bahwa dengan sebuah contoh, hal ini akan lebih mudah dipahami:
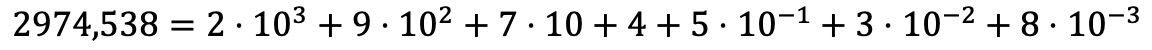
Latihan dekomposisi polinomial yang diselesaikan
Agar Anda dapat berlatih melakukan dekomposisi polinomial, kami telah menyiapkan beberapa latihan yang diselesaikan langkah demi langkah.
Jangan lupa bahwa Anda dapat mengajukan pertanyaan apa pun kepada kami di komentar! 🤔🤔🤔
Latihan 1
Lakukan penguraian polinomial dari bilangan-bilangan berikut:
![]()
![]()
![]()
![]()
Untuk mencari penguraian polinomial suatu bilangan, kalikan setiap digit bilangan tersebut dengan 10 dengan banyaknya digit di sebelah kanan, lalu jumlahkan semua perkaliannya. Belum:
![]()
![]()
![]()
![]()
Latihan 2
Temukan penguraian polinomial dari bilangan-bilangan berikut:
![]()
![]()
![]()
![]()
Untuk menguraikan suatu bilangan secara polinomial, Anda harus mengalikan setiap digit bilangan tersebut dengan sepuluh dengan banyaknya digit di sebelah kanannya, lalu menjumlahkan semua hasil kali. Belum:
![]()
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned} 3030 & = 3 \cdot 10^3+ 0\cdot 10^2 +3 \cdot 10 +0 \\[2ex] &= 3 \cdot 10^3+3 \cdot 10 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e3500d6a94685566b267e8708e8b0d7_l3.png)
![]()
![]()
Latihan 3
Hitung dekomposisi polinomial dari bilangan desimal berikut:
![]()
![]()
![]()
![]()
Dalam soal ini semua bilangan adalah desimal, jadi untuk menguraikannya Anda harus mengalikan setiap digit non-desimal dengan 10 yang dipangkatkan hingga jumlah digitnya hingga koma desimal, dan mengalikan setiap digit desimal dengan 10 yang dipangkatkan ke posisi desimalnya dengan tanda negatif.
![]()
![]()
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned} 0,82694 & = 0 + 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\\[2ex] & = 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-deb6b85265df2e98bcb5e116e19c397f_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned} 5,7201 & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+0\cdot 10^{-3}+1\cdot 10^{-4}\\[2ex] & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+1\cdot 10^{-4} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e204c24ba4f9138f503cf2c2a0e379d_l3.png)