Di halaman ini Anda akan menemukan penjelasan tentang apa itu binomial (atau teorema binomial) Newton dan apa rumusnya. Anda juga dapat melihat bagaimana hal ini dapat disederhanakan dengan segitiga Tartaglia (atau Pascal). Selain itu, Anda akan menemukan latihan langkah demi langkah untuk binomial Newton dan semua propertinya. Terakhir, kami akan menjelaskan keingintahuan di balik asal usul teorema khusus ini.
Apa binomial Newton?
Dalam matematika, binomial Newton , juga dikenal sebagai teorema binomial , adalah rumus yang memudahkan Anda menghitung pangkat binomial. Dengan kata lain, binomial Newton terdiri dari rumus yang dapat menyelesaikan persamaan aljabar bentuk (a+b).
Jelas sekali, teorema ini diambil dari nama fisikawan, matematikawan, dan filsuf Sir Isaac Newton. Namun, ada beberapa kontroversi dalam hal ini karena teks-teks Timur Tengah ditemukan di mana teorema ini sudah digunakan. Di bawah ini kita akan membahas secara mendalam asal muasal rumus matematika tersebut.
Rumus binomial Newton
Seperti yang kita lihat pada definisi binomial Newton, teorema ini digunakan untuk menyelesaikan pangkat binomial. Tapi… bagaimana binomial Newton diterapkan? Atau dengan kata lain, apa rumus binomial Newton?
Rumus matematika binomial Newton adalah sebagai berikut:
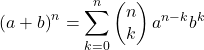
Atau setara:
![]()
Rumusnya agak rumit untuk memahami konsep binomial Newton, oleh karena itu kami telah menyajikan pangkat binomial derajat paling rendah di bawah ini agar Anda dapat lebih memahaminya:

Seperti yang Anda lihat, saat memperluas binomial , eksponen suku pertama (a) berkurang sedangkan eksponen suku kedua (b) bertambah , sama seperti elemen bawah bilangan kombinatorial bertambah.
Oleh karena itu, untuk menggunakan teorema binomial, Anda perlu mengetahui cara menyelesaikan bilangan kombinatorial, yaitu ekspresi aljabar bertipe
![]()
. Jadi, sebelum kita melihat contoh cara menghitung binomial Newton, mari kita tinjau secara singkat bilangan kombinatorial.
nomor kombinatorial
Untuk menentukan bilangan kombinatorial (atau koefisien binomial) Anda harus menerapkan rumus berikut:
![]()
Emas
![]()
Dan
![]()
Ini adalah bilangan faktorial . Ingatlah juga bahwa bilangan faktorial dihitung dengan mengalikan semua bilangan bulat positif 1 dengan bilangan tersebut:
![]()
Sebagai contoh, kita akan mencari bilangan kombinatorial sehingga Anda dapat melihat cara kerjanya:
![]()
Bilangan kombinatorial juga dapat ditentukan melalui kalkulator dengan kuncinya
![]()
Contoh Binomial Newton
Sekarang setelah kita mengetahui apa itu teorema binomial, mari kita lihat cara menerapkan rumus binomial Newton menggunakan dua contoh numerik.
Contoh 1
- Terapkan binomial Newton untuk menghitung pangkat binomial berikut:
![]()
Tentu saja, karena binomial ini dikuadratkan, maka binomial ini juga dapat diselesaikan dengan rumus identitas penting ( cara menyelesaikan identitas penting ), namun kita akan menghitungnya dengan teorema binomial sebagai contoh.
Pertama-tama, kita harus menerapkan rumus binomial Newton:
![]()
Dalam hal ini n=2, maka:
![]()
Perhatikan baik-baik, awalnya kita naikkan suku pertama (x) ke nilai maksimum yang dalam hal ini adalah 2. Sebaliknya, suku kedua (3) kita naikkan ke nilai minimum yang mungkin, yaitu selalu 0. Tapi saat kita menuju ke kanan, kita perlu menaikkan suku pertama ke angka yang lebih rendah dari sebelumnya dan suku kedua ke angka yang lebih tinggi dari sebelumnya.
Sekarang mari kita hitung bilangan kombinatorialnya:
![]()
Kami memecahkan kekuatan:
![]()
Dan terakhir, kami menghitung perkaliannya:
![]()
Contoh 2
Sekarang kita akan memecahkan masalah yang sedikit lebih sulit.
- Terapkan rumus binomial Newton untuk mencari pangkat binomial berikut:
![]()
Rumus teorema binomial adalah:
![]()
Dalam hal ini n=3, maka:
![]()
Kami menghitung bilangan kombinatorial:
![]()
Sekarang kita selesaikan pangkatnya, untuk ini penting bagi Anda untuk mengingat dua properti berikut:
• Ketika monomial dipangkatkan, koefisien dan variabelnya dipangkatkan ke eksponen yang sama →
![]()
• Suku apa pun yang dibawa ke 0 menghasilkan 1 →
![]()
Oleh karena itu kami menemukan kekuatan melalui 2 properti ini:
![]()
![]()
Dan terakhir, kita kalikan sukunya:
![]()
Binomial Newton dan segitiga Tartaglia (atau Pascal).
Seperti yang Anda lihat pada contoh di atas, menghitung bilangan kombinatorial agak membosankan. Oleh karena itu kami akan mengajari Anda trik agar Anda tidak perlu menyelesaikan bilangan kombinatorial, karena Anda bisa langsung mengetahui nilainya menggunakan segitiga Tartaglia yang disebut juga segitiga Pascal.
Jika Anda belum tahu apa itu, segitiga Tartaglia , disebut juga segitiga Pascal , adalah representasi matematis dari bilangan-bilangan yang disusun dalam bentuk segitiga.
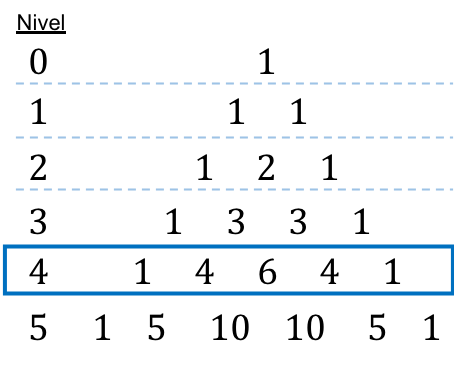
Untuk membuat segitiga Tartaglia atau Pascal, kita harus memulai dari titik sudut segitiga yang selalu 1, kemudian ditentukan banyaknya garis di bawahnya. Tiap-tiap bilangan pada baris-baris berikut sama dengan jumlah dua bilangan yang berada tepat di atasnya, kecuali ujung-ujung garis selalu 1.

Jadi, masing-masing bilangan pada segitiga Tartaglia ini sesuai dengan hasil bilangan kombinatorial, lihat gambar berikut:

Misalnya koefisien binomial
![]()
setara dengan 3, karena pada segitiga Tartaglia terdapat angka 3 pada posisinya.
Oleh karena itu, kita dapat menggunakan segitiga Tartaglia (atau Pascal) untuk menyelesaikan binomial Newton dengan lebih cepat, karena segitiga ini menghemat perhitungan bilangan kombinatorial.
Misalnya, jika kita ingin melakukan potensiasi binomial berikut:
![]()
Dengan menerapkan aturan binomial Newton kita memperoleh ekspresi aljabar berikut:
![]()
Nah, daripada menghitung bilangan kombinatorial satu per satu, kita cukup mengganti setiap bilangan kombinatorial dengan koefisien segitiga Tartaglia yang sesuai. Dalam hal ini binomial dinaikkan ke tingkat ke-3, sehingga sesuai dengan tingkat ketiga segitiga:

![]()
Dan sekarang yang harus kita lakukan hanyalah melakukan operasi selanjutnya:
![]()
![]()
Seperti yang Anda lihat, segitiga Tartaglia (atau Pascal) digunakan untuk menghitung binomial Newton dengan cara yang lebih sederhana dan cepat, seperti yang telah kami tunjukkan. Inilah mengapa kami menyarankan untuk menggunakannya.
Untuk meringkas semua yang telah kita lihat sejauh ini, kami meninggalkan Anda dengan gambar yang menunjukkan seperti apa ekspresi binomial Newton dengan bilangan segitiga Tartaglia (atau Pascal):

Binomial Newton negatif: kekuatan pengurangan
Sejauh ini semua contoh binomial Newton yang telah kita pecahkan hanyalah penjumlahan. Sebaliknya, jika salah satu dari dua suku binomial bertanda negatif, prosedurnya tetap sama namun sedikit berubah.
Jika salah satu suku binomialnya negatif, yaitu pengurangan bertipe (ab) n , maka tanda pemuaian binomial Newton harus bergantian dalam bentuk + – + – + – + – …
Di bawah ini kami telah mengembangkan pangkat binomial negatif dari 5 derajat pertama dengan teorema binomial dan koefisien segitiga Tartaglia yang sudah ada, sehingga Anda dapat langsung mencari ekspresi binomial yang Anda perlukan:

Sifat binomial Newton
Ekspresi binomial Newton memiliki ciri-ciri sebagai berikut:
- Penguraian binomial Newton selalu menghasilkan satu suku lebih banyak daripada derajat binomial tersebut. Atau dengan kata lain untuk pasangan
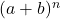
mereka terpengaruh
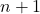
ketentuan.
- Kekuatan elemen

Dimulai dari

dan jumlahnya menurun hingga mencapai 0 pada kuartal terakhir.
- Kekuatan elemen

mereka pergi ke arah lain: mereka mulai dari 0 dan meningkat hingga mencapai

di semester terakhir.
- Untuk setiap elemen binomial Newton, jumlah eksponennya

Dan

adalah sama dengan
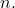
- Koefisien suku pertama ekspresi binomial Newton selalu 1 (positif) dan koefisien kedua setara dengan eksponen binomial (positif atau negatif).
Hitung suku ke-k binomial Newton
Meskipun hal ini tidak biasa, terkadang kita dapat menemui permasalahan di mana, alih-alih melakukan ekspansi binomial Newton, kita diminta menentukan suku ke-k dari binomial Newton, yaitu suku yang menempati posisi k.
Jadi, untuk menghitung suku yang menempati tempat k dalam binomial Newton, kita harus menggunakan rumus yang bergantung pada apakah binomial tersebut merupakan penjumlahan atau pengurangan:
- Jika binomial Newton positif, maka nilai suku ke-k dihitung dengan rumus berikut:
![]()
- Jika binomial Newton negatif, nilai suku ke-k ditentukan dengan rumus berikut:
![]()
Sebagai contoh, kita akan mencari suku keempat dari binomial derajat 5 berikut:
![]()
Karena ini adalah binomial yang terdiri dari penjumlahan, kami menerapkan rumus pertama:
![]()
Kami mengganti variabel dalam rumus dengan nilai yang sesuai:
![]()
Dan kami melakukan operasi:
![]()
![]()
![]()
Dan dengan cara ini kita telah menghitung suku keempat dari ekspansi binomial Newton tanpa perlu menghitung semua suku lainnya.
Latihan terpecahkan untuk binomial Newton
Sekarang setelah kami menjelaskan apa itu teorema binomial, kami memberikan kepada Anda beberapa latihan langkah demi langkah tentang binomial Newton sehingga Anda dapat berlatih. Ingat juga bahwa Anda dapat meninggalkan pertanyaan atau saran apa pun kepada kami di komentar.
Latihan 1
Perluas pangkat binomial berikut menggunakan teorema binomial:
![]()
Pertama-tama kita menggunakan rumus binomial Newton:
![]()
Karena binomial dipangkatkan 3, kita melihat segitiga Tartaglia tingkat ketiga untuk langsung mencari bilangan kombinatorialnya:

![]()
Kami menjalankan wewenang:
![]()
Dan akhirnya kita kalikan:
![]()
![]()
Latihan 2
Hitung pangkat berikut dengan rumus binomial Newton:
![]()
Pertama, kita terapkan rumus binomial Newton:
![]()
Karena binomialnya pangkat tiga, kita lihat segitiga Pascal tingkat ketiga untuk mengetahui langsung nilai bilangan kombinatorialnya:

![]()
Kami menghitung kekuatan monomial:
![]()
Dan terakhir, kita melakukan perkalian:
![]()
![]()
Latihan 3
Perluas ekspresi polinomial berikut menggunakan rumus binomial Newton:
![]()
Pertama, kita menggunakan rumus binomial Newton. Namun karena kita mempunyai pengurangan di dalam tanda kurung, kita harus mengganti tanda koefisien setiap suku:
![]()
Karena binomial dipangkatkan tiga, kita melihat tingkat ketiga segitiga Tartaglia untuk menghitung langsung bilangan kombinatorial:

![]()
Kami menjalankan wewenang:
![]()
Dan kami menyelesaikan perkaliannya:
![]()
![]()
Latihan 4
Temukan ekspresi diperluas dari binomial Newton berikut dengan rumus:
![]()
Kita harus menerapkan rumus umum untuk binomial Newton, tetapi karena dalam kasus ini kita mempunyai pengurangan dalam tanda kurung, kita harus mengganti tanda setiap suku:
![Rendered by QuickLaTeX.com \begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7a8620bd23846e1f98f7646cbd51dbc5_l3.png)
Karena binomial dinaikkan ke yang keempat, kita melihat level 4 segitiga Tartaglia untuk langsung mencari bilangan kombinatorial:
![Rendered by QuickLaTeX.com \begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-128e8baa45ddd7d74703c9dfd4a19b06_l3.png)
Kami menyadari semua kekuatan:
![]()
Dan terakhir, kita menyelesaikan perkaliannya:
![]()
![]()
Latihan 5
Tentukan suku ketujuh pada perluasan persamaan binomial berikut:
![]()
Karena ini adalah binomial negatif, kita harus menggunakan rumus berikut:
![]()
Kita ingin menentukan suku 7 dan binomialnya dipangkatkan 10, sehingga dengan mensubstitusikan nilai-nilai tersebut ke dalam rumus menjadi:
![]()
Oleh karena itu, cukup mengoperasikannya dengan mengetahui istilah:
![Rendered by QuickLaTeX.com \begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ded0622cbba2bff0563c2f9982c05142_l3.png)
Sejarah binomial Newton
Meskipun asal muasal teorema binomial dikaitkan dengan ilmuwan terkenal Inggris Isaac Newton (1642-1727), namun pada kenyataannya rumusan pertama teorema tersebut pertama kali ditemukan oleh insinyur Persia Al-Karijí sekitar tahun 1000. Dan bahkan ditemukan bahwa pada abad ke-13 ahli matematika Tiongkok Yang Hui dan Chuh Shih-Chieh sudah mengetahui ekspansi binomial derajat kecil.
Kemudian, pada abad ke-17, Newton membangun landasan yang diletakkan oleh ahli matematika sebelumnya untuk memperluas teorema binomial. Dengan menggunakan metode interpolasi dan ekstrapolasi matematikawan John Walls serta konsep eksponen umum, ia mampu mengubah ekspresi polinomial menjadi deret tak hingga.
Sekitar tahun 1665, Newton berhasil menunjukkan bahwa eksponen n dari teorema binomial bisa juga merupakan eksponen rasional, artinya pangkat binomial juga dapat diselesaikan jika eksponennya berupa pecahan. Di sisi lain juga dibuktikan pada kasus eksponen negatif. Dan yang mengejutkan, ia menemukan bahwa perkembangan kedua ekspresi tersebut merupakan rangkaian suku yang tak terhingga.
Dengan penemuan inilah Newton mulai mempertanyakan hubungan antara deret tak hingga dan ekspresi polinomial hingga, dan menyimpulkan bahwa operasi matematis dapat dilakukan dengan deret tak hingga dengan cara yang sama seperti ekspresi polinomial hingga. Meskipun Newton tidak pernah menerbitkan teorema ini, John Walls akhirnya menerbitkannya pada tahun 1685, dan memuji Newton atas penemuan ini.