Pecahan aljabar: penyederhanaan, operasi, latihan penyelesaian, dll. -

Pada halaman ini kami menjelaskan apa itu pecahan aljabar, kapan pecahan tersebut setara, cara menyederhanakannya, dan cara melakukan operasi pecahan aljabar (penjumlahan, pengurangan, perkalian, dan pembagian). Selain itu, Anda akan dapat melihat latihan langkah demi langkah yang diselesaikan untuk pecahan aljabar. Singkatnya, di sini Anda akan menemukan segala sesuatu tentang pecahan aljabar.

Apa itu pecahan aljabar?

Dalam matematika, pecahan aljabar adalah pecahan yang mempunyai polinomial pada pembilangnya dan polinomial lain pada penyebutnya.

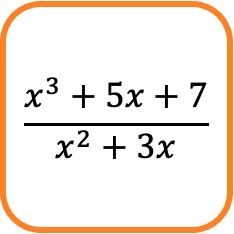
Misalnya, persamaan pecahan di atas terdiri dari pecahan aljabar karena pembilang dan penyebutnya terdiri dari polinomial.

Setara pecahan aljabar

Setelah kita mengetahui definisi pecahan aljabar, mari kita lihat apakah dua pecahan tersebut sama besarnya.

Secara matematis, dua pecahan aljabar dikatakan ekuivalen jika syarat berikut terpenuhi:

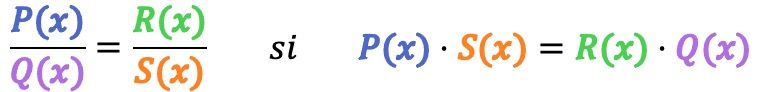
Sebagai contoh, kita akan memeriksa apakah 2 pecahan aljabar berikut ini ekuivalen:

$\cfrac{x+3}{x^2+5x+6} \qquad \cfrac{1}{x+2}$

Untuk menentukan apakah pecahan sama secara aljabar, kita mengalikan suku-sukunya secara melintang:

$(x+3)\cdot (x+2) = (x^2+5x+6)\cdot 1$

Sekarang mari kita hitung perkalian polinomial:

$x^2+2x+3x+6 = x^2+5x+6$

$x^2+5x+6 = x^2+5x+6$

Kita mendapatkan ekspresi yang sama pada kedua sisi persamaan, jadi keduanya sebenarnya merupakan dua pecahan aljabar yang ekuivalen.

Sederhanakan pecahan aljabar

Untuk menyederhanakan pecahan aljabar, pertama-tama Anda harus memfaktorkan polinomial-polinomial pada pembilang dan penyebutnya, kemudian menghilangkan faktor-faktor yang mempunyai kesamaan.

Tentunya, untuk menyederhanakan pecahan aljabar, penting bagi Anda untuk mengetahui apa itu pemfaktoran polinomial dan cara melakukannya. Jika Anda masih belum mengetahui cara memfaktorkan polinomial atau tidak mengingatnya sepenuhnya, saya sarankan untuk membuka halaman tertaut sebelum melanjutkan, jika tidak, Anda hampir tidak akan memahami prosedurnya. Ini menjelaskan langkah demi langkah cara memfaktorkan polinomial dan, sebagai tambahan, Anda akan dapat melihat beberapa contoh dan berlatih dengan latihan yang diselesaikan.

Sekarang mari kita lihat bagaimana pecahan aljabar disederhanakan dengan menerapkan metode pemfaktoran polinomial menggunakan sebuah contoh:

Sederhanakan pecahan aljabar berikut:

$\cfrac{x^3+2x^2-x-2}{x^2-2x+1}$

Pertama, kita memfaktorkan polinomial pembilang dan penyebut pecahan:

$\cfrac{(x-1)(x+1)(x+2)}{(x-1)(x-1)}$

⬆(Jika Anda tidak tahu cara memfaktorkan polinomial, lihat tautan di atas)⬆

Dan setelah kita memfaktorkan polinomialnya, kita menghilangkan faktor persekutuan antara pembilang dan penyebutnya, yaitu, kita menghilangkan semua suku yang berulang:

$\cfrac{\cancel{(x-1)}(x+1)(x+2)}{\cancel{(x-1)}(x-1)}$

Oleh karena itu, pecahan aljabar yang disederhanakan terlihat seperti ini:

$\cfrac{(x+1)(x+2)}{x-1}$

Dalam soal ini, polinomial pecahan aljabar difaktorkan dengan mencari akar-akarnya; namun, terkadang polinomial dapat difaktorkan secara langsung dengan mengambil faktor persekutuannya (metode yang jauh lebih cepat). Di tautan ini Anda akan melihat apa artinyamengambil faktor persekutuan dari polinomial dan Anda akan menemukan cara menyederhanakan pecahan aljabar menggunakan faktor persekutuan.

Operasi dengan pecahan aljabar

Seperti jenis pecahan lainnya, operasi juga dapat dilakukan dengan pecahan aljabar. Secara spesifik, pecahan aljabar dapat dijumlahkan, dikurangi, dikalikan, dan dibagi. Di bawah ini kami menjelaskan langkah demi langkah dengan contoh bagaimana setiap jenis operasi dihitung.

Penjumlahan dan pengurangan pecahan aljabar

Tata cara penjumlahan dan pengurangan pecahan aljabar pada dasarnya sama, jadi kita akan menganalisisnya bersama-sama. Pertama kita akan melihat contoh penjumlahan dua pecahan aljabar, dan di bawah ini kita akan mempelajari perbedaan metode pengurangan pecahan aljabar.

Menjumlahkan pecahan aljabar

Penjumlahan pecahan aljabar dilakukan dengan cara yang sama seperti pada pecahan biasa: pertama-tama kurangi pecahan menjadi penyebut yang sama, lalu tambahkan pembilangnya.

Mari kita lihat bagaimana pecahan aljabar dijumlahkan menggunakan contoh:

$\cfrac{x}{x^2+2x+1} + \cfrac{3x}{x^2+x}$

Pertama-tama kita memfaktorkan penyebut pecahan tersebut:

$\cfrac{x}{(x+1)(x+1)} + \cfrac{3x}{x(x+1)}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Sekarang kita perlu mencari lcm (kelipatan persekutuan terkecil) dari penyebutnya untuk mereduksi pecahan menjadi penyebut yang sama.

Tip: KPK dari penyebut-penyebutnya selalu dibentuk dari hasil kali faktor- faktor persekutuannya, dikalikan dengan pangkat terbesarnya .

Misalnya, dalam kasus kami

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Pembagi persekutuan antara penyebut yang dipangkatkan ke pangkat terbesar adalah

$(x+1)^2.$

Dan faktor bukan persekutuan antara penyebutnya adalah

$x.$

Oleh karena itu, KPK dari penyebutnya dalam hal ini adalah:

$(x+1)^2 \cdot x$

Oleh karena itu, KPK dari penyebutnya adalah

$(x+1)^2 \cdot x,$

oleh karena itu ini akan menjadi penyebut baru dari 2 pecahan.

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{}{x(x+1)^2} + \cfrac{}{x(x+1)^2}$

Setelah kita menemukan penyebutnya, kita harus memodifikasi pembilangnya. Untuk melakukannya, kita mengikuti proses yang sama seperti pada penjumlahan pecahan normal: untuk setiap pecahan kita membagi lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

antara penyebut aslinya dan kalikan hasilnya dengan pembilangnya:

$\cfrac{x(x+1)^2}{(x+1)^2} = \cfrac{x\cancel{(x+1)^2}}{\cancel{(x+1)^2}} = \color{red}\bm{x}$

$\cfrac{x(x+1)^2}{x(x+1)}= \cfrac{\cancel{x}(x+1)^\cancel{2}}{\cancel{x}\cancel{(x+1)}}=\color{blue} \bm{x+1}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{x \cdot \color{red}\bm{x} \color{black} }{x(x+1)^2} + \cfrac{3x \cdot \color{blue} \bm{(x+1)} \color{black}}{x(x+1)^2}$

Sekarang kita dapat menggabungkan kedua pecahan tersebut karena penyebutnya sama:

$\cfrac{x^2+3x(x+1)}{x(x+1)^2}$

Terakhir, kami mengoperasikan pembilangnya. Pertama-tama kita kerjakan hasil kali monomial dan polinomialnya:

$\cfrac{x^2 +3x\cdot x+ 3x\cdot 1 }{x(x+1)^2}$

$\cfrac{x^2 +3x^2 + 3x }{x(x+1)^2}$

Selanjutnya, kita tambahkan suku serupa ke pembilangnya:

$\cfrac{4x^2 + 3x }{x(x+1)^2}$

Biasanya kita sudah sampai di sana, tapi jika kita melihat soal ini lebih dekat, kita bisa menyederhanakan pecahan aljabar lebih jauh lagi dengan menghilangkan faktor persekutuan dari pembilangnya. Belum:

$\cfrac{x(4x + 3)}{x(x+1)^2}$

$\cfrac{\cancel{x}(4x + 3)}{\cancel{x}(x+1)^2}$

$\cfrac{4x + 3}{(x+1)^2}$

Jadi kita telah menyelesaikan penjumlahan kedua pecahan aljabar tersebut.

Pengurangan pecahan aljabar

Untuk mengurangkan pecahan aljabar, kita harus mengikuti prosedur yang mirip dengan menjumlahkan pecahan aljabar: pertama-tama kurangi pecahan tersebut menjadi penyebut yang sama, lalu kurangi pembilangnya.

Mari kita lihat bagaimana pecahan aljabar dikurangkan dengan sebuah contoh:

$\cfrac{2x}{x^2-x-6} - \cfrac{4x-3}{(x+2)^2}$

Pertama, kita perlu memfaktorkan penyebut kedua pecahan tersebut:

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2}$

Seperti halnya pengurangan pecahan biasa, sekarang kita harus menghitung lcm (kelipatan persekutuan terkecil) penyebutnya untuk mereduksi pecahan menjadi penyebut yang sama. Dalam hal ini, KPK dari penyebutnya adalah

$(x+2)^2(x-3) ,$

oleh karena itu ini akan menjadi penyebut baru dari 2 pecahan.

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{}{(x+2)^2(x-3)} + \cfrac{}{(x+2)^2(x-3)}$

Sekarang kita menerapkan proses yang sama seperti mengurangkan pecahan biasa: untuk setiap pecahan kita membagi lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

antara penyebut aslinya dan kalikan hasilnya dengan pembilangnya:

$\cfrac{(x+2)^2(x-3)}{(x+2)(x-3)} = \cfrac{(x+2)^{\cancel{2}}\cancel{(x-3)}}{\canel{(x+2)}\cancel{(x-3)}} = \color{red}\bm{x+2}$

$\cfrac{(x+2)^2(x-3)}{(x+2)^2}= \cfrac{\cancel{(x+2)^2}(x-3)}{\cancel{(x+2)^2}}=\color{blue} \bm{x-3}$

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{2x\cdot \color{red}\bm{(x+2)} \color{black}}{(x+2)^2(x-3)} + \cfrac{(4x-3)\cdot \color{blue} \bm{(x-3)} \color{black}}{(x+2)^2(x-3)}$

Sekarang kita gabungkan dua pecahan aljabar karena penyebutnya sama:

$\cfrac{2x(x+2)-(4x-3)(x-3)}{(x+2)^2(x-3)}$

Dan kami beroperasi pada pembilangnya. Pertama-tama kita selesaikan perkalian polinomial:

$\cfrac{2x^2+4x-\bigl[4x^2-12x-3x+9\bigr]}{(x+2)^2(x-3)}$

Kesalahan yang sangat umum terjadi saat mengurangkan pecahan aljabar adalah lupa memberi tanda kurung setelah melakukan perkalian ini. Ini merupakan kesalahan karena tanda negatif mempengaruhi semua elemen hasil perkalian, bukan hanya suku pertama.

Kami melakukan operasi dalam tanda kurung:

$\cfrac{2x^2+4x-\bigl[4x^2-15x+9\bigr]}{(x+2)^2(x-3)}$

Jadi, berkat tanda negatifnya, kita mengubah tanda semua suku dalam tanda kurung:

$\cfrac{2x^2+4x-4x^2+15x-9}{(x+2)^2(x-3)}$

Dan terakhir, kami mengelompokkan monomial serupa:

$\cfrac{-2x^2+19x-9}{(x+2)^2(x-3)}$

Perkalian pecahan aljabar

Untuk mengalikan pecahan aljabar, pertama-tama kita memfaktorkan semua polinomial dari pecahan tersebut, kemudian kita mengalikan pembilangnya satu sama lain dan penyebutnya satu sama lain, dan terakhir kita sederhanakan pecahan yang diperoleh.

Oleh karena itu, hasil kali pecahan aljabar sebenarnya dihitung dengan cara yang sama seperti hasil kali pecahan biasa.

Selanjutnya mari kita lihat cara mengalikan dua pecahan aljabar dengan contoh:

$\cfrac{3x}{x^2+x-2} \cdot \cfrac{x^2-6x+5}{x+1}$

Pertama-tama Anda harus memfaktorkan semua polinomial pecahan, baik pembilang maupun penyebutnya:

$\cfrac{3x}{(x-1)(x+2)} \cdot \cfrac{(x-1)(x-5)}{x+1}$

Sekarang mari kita mengalikan pecahan. Untuk melakukan ini, kita mengalikan pembilang dan penyebutnya:

$\cfrac{3x \cdot (x-1)(x-5)}{(x-1)(x+2)\cdot (x+1)}$

$\cfrac{3x(x-1)(x-5)}{(x-1)(x+2)(x+1)}$

Dan terakhir, kita sederhanakan faktor-faktor yang berulang pada penyebut dan pembilangnya:

$\cfrac{3x\cancel{(x-1)}(x-5)}{\cancel{(x-1)}(x+2)(x+1)}$

Maka hasil perkaliannya adalah:

$\cfrac{3x(x-5)}{(x+2)(x+1)}$

Pecahan tersebut tidak dapat disederhanakan lagi. Jadi kita sudah selesai mengalikan pecahan aljabar.

Pembagian pecahan aljabar

Untuk menghitung pembagian pecahan aljabar , pertama-tama kita memfaktorkan semua polinomialnya, kemudian kita mengalikan pecahan tersebut secara melintang (pembilang pertama dengan penyebut kedua dan penyebut pertama dengan pembilang kedua) dan terakhir, kita menyederhanakan pecahan aljabar.

Jadi mari kita lihat lebih baik bagaimana dua pecahan aljabar dibagi dengan menggunakan contoh:

$\cfrac{x^3-7x-6}{2x^2-8} : \cfrac{x^2+2x+1}{6}$

Langkah pertama dalam membagi dua pecahan aljabar adalah dengan memfaktorkan semua polinomial yang terlibat dalam operasi tersebut:

$\cfrac{(x+1)(x+2)(x-3)}{2(x-2)(x+2)} : \cfrac{(x+1)^2}{6}$

Sekarang kita perlu membagi pecahannya. Caranya, kita mengalikan pecahan secara melintang, yaitu pembilang pertama dikalikan dengan penyebut kedua dan hasilnya adalah pembilang pecahan baru, dan dengan cara yang sama, penyebut pertama dikalikan dengan pembilang kedua. dan hasilnya adalah penyebut pecahan baru:

$\cfrac{(x+1)(x+2)(x-3)\cdot 6}{2(x-2)(x+2)\cdot (x+1)^2}$

$\cfrac{6(x+1)(x+2)(x-3)}{2(x-2)(x+2)(x+1)^2}$

Mari kita sederhanakan faktor-faktor yang berulang pada penyebut dan pembilangnya:

$\cfrac{6\cancel{(x+1)}\cancel{(x+2)}(x-3)}{2(x-2)\cancel{(x+2)}(x+1)^\cancel{2}}$

$\cfrac{6(x-3)}{2(x-2)(x+1)}$

Dan kita dapat menyederhanakan pecahan lebih jauh lagi

$6:2 = 3.$

$\cfrac{3(x-3)}{(x-2)(x+1)}$

Pecahan tersebut tidak dapat disederhanakan lagi. Oleh karena itu, kita telah membagi pecahan aljabar.

Latihan soal pecahan aljabar

Di bawah ini kami menawarkan kepada Anda beberapa latihan yang diselesaikan selangkah demi selangkah tentang pecahan aljabar, sehingga Anda dapat berlatih dan menyelesaikan pemahaman konsepnya. Jangan lupa Anda dapat mengajukan pertanyaan apa pun kepada kami di bawah di komentar! 💬💬💬

Latihan 1

Tentukan apakah pecahan aljabar berikut ekuivalen atau tidak:

$\cfrac{x+3}{x^2-9} \qquad \cfrac{1}{x-3} \qquad \cfrac{x-3}{x^2+2x-3}$

Lihat solusinya

Untuk memeriksa apakah dua pecahan aljabar setara, Anda harus mengalikannya secara melintang dan melihat apakah Anda memperoleh persamaan. Jadi kita periksa dulu pecahan pertama dan kedua:

$\cfrac{x+3}{x^2-9}= \cfrac{1}{x-3} \quad ?$

$(x+3)\cdot (x-3)=(x^2-9)\cdot 1$

Kami memecahkan identitas penting di sebelah kiri persamaan:

$x^2-9=x^2-9$

✅

Dalam hal ini, kita memperoleh persamaan, sehingga pecahan pertama dan kedua sama secara aljabar.

Kami sekarang menerapkan prosedur yang sama dengan pecahan aljabar pertama dan ketiga:

$\cfrac{x+3}{x^2-9}= \cfrac{x-3}{x^2+2x-3} \quad ?$

$(x+3)\cdot (x^2+2x-3)=(x^2-9)\cdot(x-3)$

$x^3+2x^2-3x+3x^2+6x-9=x^3-3x^2-9x+27$

$x^3+5x^2+3x-9=x^3-3x^2-9x+27$

❌

Namun kali ini pecahan aljabarnya tidak memenuhi persamaan, sehingga pecahan pertama dan ketiga berbeda secara matematis.

Kesimpulannya, pecahan ketiga berbeda dengan pecahan pertama sehingga juga tidak sama dengan pecahan kedua karena pecahan pertama dan kedua ekuivalen.

$\cfrac{x+3}{x^2-9} = \cfrac{1}{x-3} \neq \cfrac{x-3}{x^2+2x-3}$

Latihan 2

Sederhanakan pecahan aljabar berikut:

$\text{A)} \ \cfrac{5x^2+10x}{11x}$

$\text{B)} \ \cfrac{x^2-4}{x^2+2x-8}$

$\text{C)} \ \cfrac{x^3-2x^2-3x}{x^2-3x}$

$\text{D)} \ \cfrac{x^3-3x+2}{x^3+4x^2+x-6}$

Lihat solusinya

Untuk menyederhanakan pecahan aljabar, kita perlu memfaktorkan polinomial pada pembilang dan penyebutnya, lalu menghilangkan faktor berulangnya. Belum:

$\text{A)} \ \begin{array}{l} \cfrac{5x^2+10x}{11x} =\cfrac{5x(x+2)}{11x} = \\[4ex] =\cfrac{5\cancel{x}(x+2)}{11\cancel{x}}= \cfrac{\bm{5(x+2)}}{\bm{11}}\end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{x^2-4}{x^2+2x-8} = \cfrac{(x-2)(x+2)}{(x-2)(x+4)}= \\[4ex] = \cfrac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}(x+4)}=\cfrac{\bm{x+2}}{\bm{x+4}}}\end{array}$

$\text{C)} \ \begin{array}{l} \cfrac{x^3-2x^2-3x}{x^2-3x} = \cfrac{x(x+1)(x-3)}{x(x-3)}}= \\[4ex] = \cfrac{\cancel{x} (x+1) \cancel{x-3}}{\cancel{x}\cancel{(x-3)}} = \cfrac{x+1}{1} = \\[4ex] = \bm{x+1}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^3-3x+2}{x^3+4x^2+x-6}=\cfrac{(x-1)^2(x+2)}{(x-1)(x+3)(x+2)}= \\[4ex] = \cfrac{(x-1)^{\cancel{2}}\cancel{(x+2)}}{\cancel{(x-1)}(x+3)\cancel{(x+2)}}=\cfrac{\bm{x-1}}{\bm{x+3}}\end{array}$

Latihan 3

Hitung penjumlahan dan pengurangan pecahan aljabar berikut:

$\text{A)} \ \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6}$

$\text{B)} \ \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4}$

$\text{C)} \ \cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}$

$\text{D)} \ x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}$

Lihat solusinya

Untuk menjumlahkan (atau mengurangi) pecahan aljabar, pertama-tama kita harus mengurangkan pecahan tersebut menjadi penyebut yang sama, lalu menjumlahkan (atau mengurangi) pembilangnya. JADI:

$\text{A)} \ \begin{array}{l} \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6} = \cfrac{4}{x(x+2)} + \cfrac{3x-2}{(x+2)(x-3)} = \\[4ex] =\cfrac{4\cdot(x-3)}{x(x+2)\cdot (x-3)} + \cfrac{(3x-2)\cdot x}{(x+2)(x-3)\cdot x} = \cfrac{4\cdot(x-3) + (3x-2)\cdot x}{x(x+2)(x-3)} = \\[4ex] = \cfrac{4x-12 + 3x^2-2x}{x(x+2)(x-3)} = \cfrac{ \bm{3x^2+2x-12}}{\bm{x(x+2)(x-3)}} \end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4} = \cfrac{4x}{x(x+1)^2} - \cfrac{2}{(x+1)(x-4)}= \\[4ex] = \cfrac{4x \cdot (x-4)}{x(x+1)^2 \cdot (x-4)} - \cfrac{2 \cdot (x+1) \cdot x}{(x+1)^2(x-4)\cdot x}= \cfrac{4x \cdot (x-4) - 2 \cdot (x+1) \cdot x }{x(x+1)^2 (x-4) }= \\[4ex] = \cfrac{4x^2 -16x - 2 \cdot (x^2+x) }{x(x+1)^2 (x-4) }= \cfrac{4x^2 -16x - 2x^2 - 2x }{x(x+1)^2 (x-4) } =\\[4ex] =\cfrac{2x^2 -18x}{x(x+1)^2 (x-4)}=\cfrac{x(2x -18)}{x(x+1)^2 (x-4)}= \\[4ex] = \cfrac{\bm{2x -18}}{\bm{(x+1)^2 (x-4)}}\end{array}$

$\text{C)} \ \begin{array}{l}\cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}=\cfrac{7x}{(x-2)^2} + \cfrac{-5}{x-2}} = \\[4ex] = \cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)\cdot (x-2)}=\cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)^2}= \\[4ex] = \cfrac{7x + [-5\cdot (x-2)] }{(x-2)^2} =\cfrac{7x -5\cdot (x-2) }{(x-2)^2} = \\[4ex] = \cfrac{7x -5x+10 }{(x-2)^2} = \cfrac{ \bm{2x+10}}{\bm{(x-2)^2 } } \end{array}$

$\text{D)} \ \begin{array}{l} x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}=\cfrac{x}{1} +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}= \\[4ex] =x +\cfrac{-3x}{(x-2)(x+2)} - \cfrac{2x^3-1}{2(x+1)(x+2)}= \\[4ex] = \cfrac{x\cdot 2(x-2)(x+2)(x+1)}{1\cdot 2(x-2)(x+2)(x+1)} \ + \ \cfrac{-3x\cdot 2(x+1)}{(x-2)(x+2)\cdot 2(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x+1)(x+2)\cdot (x+1)}= \\[4ex] = \cfrac{ 2x(x-2)(x+2)(x+1)}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x(x+1)}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x-2)(x+2)(x+1)}= \\[4ex]= \cfrac{ 2x^4+2x^3-8x^2-8x}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x^2-6x}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{2x^4-4x^3-x+2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - (2x^4-4x^3-x+2)}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - 2x^4+4x^3+x-2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ \bm{6x^3-14x^2-13x-2}}{\bm{2(x-2)(x+2)(x+1)}}\end{array}$

Latihan 4

Selesaikan perkalian dan pembagian pecahan aljabar berikut:

$\text{A)} \ \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1}$

$\text{B)} \ \cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3}$

$\text{C)} \ \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}$

$\text{D)} \ \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2}$

Lihat solusinya

Untuk mengalikan pecahan aljabar, pertama-tama kita harus memfaktorkan semua polinomialnya, kemudian mengalikan pembilang dan penyebutnya, dan terakhir menyederhanakan pecahan yang dihasilkan.

$\text{A)} \ \begin{array}{l} \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1} = \cfrac{(x+1)(x+4)}{7}\cdot \cfrac{x-1}{(x-1)(x+1)}\\[4ex] =\cfrac{(x+1)(x+4)\cdot (x-1)}{7 \cdot (x-1)(x+1)}=\cfrac{(x+1)(x+4) (x-1)}{7(x-1)(x+1)} = \\[4ex] = \cfrac{\cancel{(x+1)}(x+4)\cancel{ (x-1)}}{7\cancel{(x-1)}\cancel{(x+1)}} = \cfrac{\bm{x+4}}{\bm{7}}\end{array}$

$\text{B)} \ \begin{array}{l}\cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3} = \cfrac{3(x+2)(x+3)}{3x}\cdot \cfrac{(x-1)(x+2)}{(x-1)(x+1)(x+3)}= \\[4ex] =\cfrac{3(x+2)(x+3)\cdot (x-1)(x+2)}{3x\cdot (x-1)(x+1)(x+3)}=\cfrac{3(x+2)(x+3) (x-1)(x+2)}{3x (x-1)(x+1)(x+3)} = \\[4ex] = \cfrac{\cancel{3}(x+2)\cancel{(x+3)} \cancel{(x-1)}(x+2)}{\cancel{3}x \cancel{(x-1)}(x+1)\cancel{(x+3)}} = \cfrac{(x+2)(x+2)}{x (x+1)} = \\[4ex] = \cfrac{\bm{(x+2)^2}}{\bm{x (x+1)}}\end{array}$

Sebaliknya, untuk membagi pecahan aljabar, pertama-tama kita memfaktorkan semua polinomialnya, kemudian kita mengalikan pecahan tersebut secara melintang (pembilang pertama dengan penyebut kedua dan penyebut pertama dengan pembilang kedua) dan terakhir, kita menyederhanakan pecahan aljabar yang ditemukan.

$\text{C)} \ \begin{array}{l} \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}= \cfrac{3x}{(x+5)^2}:\cfrac{2x}{(x-5)(x+5)}=\\[4ex] = \cfrac{3x\cdot (x-5)(x+5)}{(x+5)^2\cdot 2x}=\cfrac{3x(x-5)(x+5)}{2x(x+5)^2 }= \\[4ex] =\cfrac{3\cancel{x}(x-5)\cancel{(x+5)}}{2\cancel{x}(x+5)^\cancel{2}} = \cfrac{\bm{3(x-5)}}{\bm{2(x+5)}}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2} = \cfrac{(x+3)(x+5)}{4x}:\cfrac{(x-1)(x+5)}{2x^2}= \\[4ex] = \cfrac{(x+3)(x+5)\cdot 2x^2 }{4x \cdot (x-1)(x+5)} = \cfrac{2x^2 (x+3)(x+5)}{4x (x-1)(x+5)} = \\[4ex] = \cfrac{2x^{\cancel{2}}(x+3)\cancel{ (x+5)}}{4\cancel{x} (x-1)\cancel{ (x+5)}} =\cfrac{2x(x+3)}{4(x-1)} = \cfrac{\bm{x(x+3)}}{\bm{2(x-1)}}\end{array}$

Bagaimana menurut Anda penjelasannya? Apakah kamu menyukainya? Atau apakah Anda punya saran? 💬 Beri tahu kami pendapat Anda tentang halaman ini di komentar! Kami membacakan semuanya untuk Anda! 👀 Dan jangan lupa bahwa Anda juga dapat menanyakan semua pertanyaan Anda kepada kami! ❔👇❔👇

Pecahan aljabar: penyederhanaan, operasi, latihan penyelesaian,…

Apa itu pecahan aljabar?

Setara pecahan aljabar

Sederhanakan pecahan aljabar

Operasi dengan pecahan aljabar

Penjumlahan dan pengurangan pecahan aljabar

Menjumlahkan pecahan aljabar

Pengurangan pecahan aljabar

Perkalian pecahan aljabar

Pembagian pecahan aljabar

Latihan soal pecahan aljabar

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Tinggalkan Komentar Batalkan Balasan