▷ Cara menghilangkan (atau mengekstrak) faktor persekutuan ✅ (latihan terselesaikan)

Di halaman ini kami menjelaskan cara mengambil (atau mengekstrak) faktor persekutuan dari suatu polinomial. Di sini Anda akan menemukan berbagai jenis faktor persekutuan dan Anda akan dapat melihat beberapa contoh bagaimana hal ini dicapai. Selain itu, Anda dapat berlatih dengan latihan yang diselesaikan selangkah demi selangkah.

Apa faktor persekutuannya?

Dalam matematika, faktor persekutuan adalah faktor yang terdapat pada semua suku suatu polinomial, yaitu faktor persekutuan terdiri dari suatu bilangan atau huruf yang mengalikan setiap suku suatu polinomial.

Sebagai contoh, kita akan mengetahui faktor persekutuan dari polinomial berikut:

$4x+4y$

Di nomor 4 diulangi di semua suku polinomial:

$\color{red} \bm{4} \color{black} x + \color{red} \bm{4} \color{black} y$

Oleh karena itu, faktor persekutuan polinomial ini sama dengan 4.

$\displaystyle \text{Factor com\'un} = 4 {\phantom{\frac{1}{2}}$

Cara mendapatkan (atau mengekstrak) faktor persekutuan

Setelah kita mengetahui arti faktor persekutuan, mari kita lihat cara mendapatkan faktor persekutuan dari polinomial.

Jika dua atau lebih suku suatu polinomial memiliki faktor persekutuan, faktor persekutuan tersebut dapat diambil (atau diekstraksi) untuk mengubah penjumlahan atau pengurangan polinomial tersebut menjadi perkalian.

Ini mungkin tampak agak sulit untuk ditulis, jadi mari kita lihat cara mengekstrak faktor persekutuan dari polinomial dengan sebuah contoh:

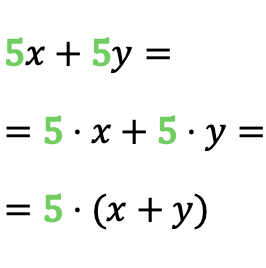
mengekstrak atau menghapus faktor persekutuan dari polinomial

Seperti yang bisa kamu lihat pada contoh, angka 5 diulang pada monomial 5x dan monomial 5y, jadi faktor persekutuan dari polinomial tersebut adalah 5. Jadi, setelah kita mengidentifikasi faktor persekutuannya, kita dapat mengonversi jumlah monomial menjadi a produk.

Jangan lupa memberi tanda kurung saat mengekstrak faktor persekutuannya, karena faktor persekutuannya harus mengalikan semua penjumlahannya.

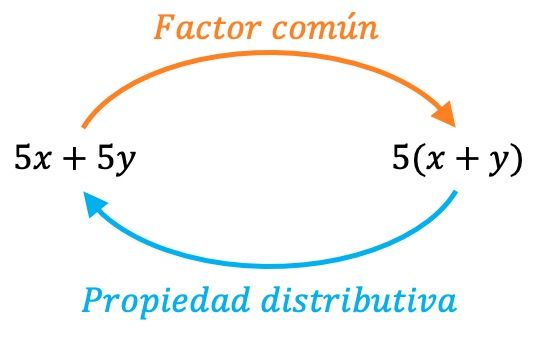
Menghilangkan faktor persekutuan adalah operasi kebalikan dari sifat distributif , yaitu kita menerapkan sifat distributif secara terbalik. Oleh karena itu, kami selalu dapat memverifikasi bahwa kami telah mengekstraksi faktor persekutuan dengan benar dengan melakukan proses sebaliknya:

Jika dengan menerapkan sifat distributif kita memperoleh polinomial yang sama dari awal, berarti kita telah memperoleh faktor persekutuannya dengan benar.
Sebaliknya, jika hasil penggunaan sifat distributif adalah polinomial lain yang berbeda dengan polinomial aslinya, berarti kita telah melakukan kesalahan dalam proses mengekstraksi faktor persekutuannya.

faktor persekutuan dan sifat distributif

Contoh Pengambilan Faktor Umum (atau Ekstraksi)

Kami memberi Anda lebih banyak contoh untuk menyelesaikan pemahaman konsep faktor persekutuan:

Contoh 1

Seperti yang Anda lihat dalam contoh ini, faktor persekutuan dapat diekstraksi dari lebih dari dua suku sekaligus:

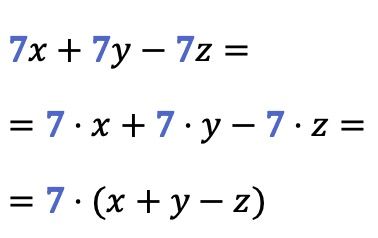
Contoh 2

Anda juga dapat mengekstrak faktor persekutuan dari variabel (atau huruf):

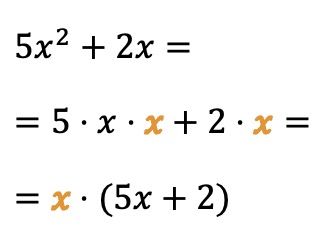
ekstrak faktor persekutuan dalam ekspresi aljabar

Dalam hal ini, huruf x mengalikan dua suku polinomial, sehingga kita dapat menyederhanakan ekspresi aljabarnya dengan mengambil variabel x sebagai faktor persekutuan.

Contoh 3

Dalam contoh ini, suku pertama variabel x dipangkatkan 3 dan suku kedua x dipangkatkan 2, sehingga kedua suku mempunyai dua x. Oleh karena itu, faktor persekutuannya bukan hanya x, tetapi x ² :

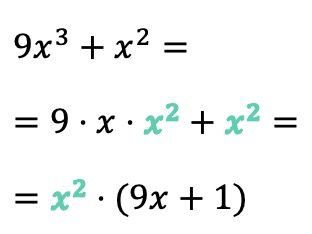
Di sisi lain, perhatikan bahwa jika faktor persekutuan dari polinomial tersebut sama persis dengan suatu suku, ketika kita mengekstrak faktor persekutuannya, kita harus menempatkan 1 sebagai gantinya . Jika tidak, jika kita tidak menempatkan apa pun pada tempatnya, kita tidak akan mendapatkan ekspresi yang setara.

cara mengekstrak atau mencari faktor persekutuan

Contoh 4

Terkadang faktor persekutuan tidak begitu jelas dan tidak terlihat secara langsung, melainkan merupakan pembagi koefisien monomial. Misalnya, faktor persekutuan pada contoh berikut adalah 3, karena penguraian faktorial dari 6 dan 9 berisi 3:

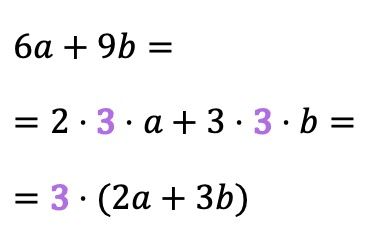
Jenis faktor persekutuan ini dalam beberapa buku aljabar disebut faktor persekutuan maksimum , karena faktor persekutuan sekaligus merupakan faktor persekutuan terbesar (PBB) dari koefisien suku-suku polinomial.

Jika Anda sudah sampai sejauh ini, itu berarti Anda mungkin sudah mengetahui cara mencari faktor persekutuan suatu polinomial, sempurna. Namun, pernahkah Anda bertanya-tanya apa gunanya faktor persekutuan? Nah, salah satu penerapan faktor persekutuan adalah digunakan untuk memfaktorkan polinomial. Jika Anda masih belum mengetahuinya, di tautan ini Anda dapat melihat apa itu faktorisasi polinomial dan mengapa faktor persekutuan sangat penting untuk melakukan operasi polinomial ini.

Faktor persekutuan pecahan

Faktor persekutuan juga sangat berguna untuk menyederhanakan suku-suku menjadi pecahan yang pembilang dan penyebutnya polinomial.

Untuk melihat cara kerjanya, mari kita sederhanakan pecahan berikut sebagai contoh:

$\cfrac{2x^2+4}{14x+8y}$

Hal pertama yang perlu kita lakukan adalah mencari faktor persekutuan dari polinomial pembilang dan polinomial penyebutnya. Dalam hal ini, faktor persekutuan kedua polinomial tersebut adalah 2:

$\cfrac{\color{red} \bm{2} \color{black}\cdot x^2+\color{red} \bm{2} \color{black}\cdot 2 }{\color{red} \bm{2} \color{black}\cdot 7x+\color{red} \bm{2} \color{black} \cdot 4y}$

Sekarang mari kita ekstrak faktor persekutuan kedua polinomial tersebut:

$\cfrac{\color{red} \bm{2} \color{black}\left(x^2+2\right)}{\color{red} \bm{2} \color{black}\left(7x+4y\right)}$

Dan setelah kita memperoleh faktor persekutuan untuk kedua polinomial, kita perlu menghilangkan faktor-faktor yang berulang pada pembilang dan penyebutnya :

$\cfrac{\cancel{2}\left(x^2+2\right)}{ \cancel{2}\left(7x+4y\right)}$

Kesimpulannya, pecahan yang disederhanakan adalah:

$\cfrac{x^2+2}{7x+4y}$

Faktor persekutuan dengan mengelompokkan

Salah satu cara untuk mereduksi suku-suku suatu polinomial adalah dengan menggunakan metode faktor persekutuan dengan mengelompokkan suku-sukunya , disebut juga ekstraksi faktor persekutuan ganda. Seperti namanya, prosedur ini terdiri dari penyederhanaan ekspresi polinomial dengan mengelompokkan suku-sukunya dua kali.

Metode ini agak rumit, jadi mari kita lihat penerapannya langkah demi langkah dengan polinomial berikut:

$x^2+2x+5x+10$

Pertama-tama kita perlu menentukan dua kemungkinan faktor persekutuan yang berbeda, jadi kita pisahkan polinomialnya menjadi dua bagian:

$(x^2+2x)+(5x+10)$

Dalam hal ini, unsur x ² dan 2x memiliki huruf x sebagai faktor persekutuan, dan suku 5x dan 10 memiliki 5 sebagai faktor persekutuan (karena 10 adalah kelipatan 5). Jadi kita mempunyai dua faktor yang sama:

$(x\cdot x+2\cdot x)+(5\cdot x+5\cdot 2)$

$x(x+2)+5(x+2)$

Dan terakhir, karena dua hasil kali polinomial yang tersisa memiliki faktor (x+2), kita dapat menyederhanakan polinomial tersebut sebagai berikut:

$(x+2)\cdot (x+5)$

Seperti yang Anda lihat, cara ini sama sekali tidak mudah. Jadi jangan ragu untuk menanyakan pertanyaan apa pun kepada kami di komentar, dan kami akan menjawabnya sesegera mungkin.

Latihan faktor umum diselesaikan selangkah demi selangkah

Kami meninggalkan Anda latihan beberapa langkah demi langkah yang diselesaikan sehingga Anda dapat berlatih mengekstraksi faktor persekutuan dari polinomial.

Latihan 1

Ekstrak faktor persekutuan dari polinomial berikut:

$\text{A)} \ 6a+6b$

$\text{B)} \ 3x^2+8x$

$\text{C)} \ 2x-4$

$\text{D)} \ -5x^4+x^2$

Lihat solusinya

A) Semua suku yang menyusun polinomial pertama mempunyai 6, jadi faktor persekutuan polinomial tersebut adalah 6:

$6a+6b = 6\cdot a + 6 \cdot b = \bm{6\cdot (a+b)}$

B) Pada polinomial kedua, semua elemennya paling sedikit memiliki satu huruf x. Berikut adalah faktor persekutuan dari polinomial tersebut:

$3x^2+8x = 3x \cdot x+8\cdot x= \bm{x\cdot (3x+8)}$

C) Monomial pertama dari polinomial tersebut jelas mempunyai 2, dan monomial kedua adalah kelipatan 2. Jadi faktor persekutuan dari polinomial tersebut adalah 2:

$2x-4= 2\cdot x - 2\cdot 2 =\bm{2\cdot (x-2)}$

D) Pada polinomial terakhir, semua variabel setidaknya dikuadratkan. Oleh karena itu, faktor persekutuannya adalah x ² :

$-5x^4+x^2= -5x^2\cdot x^2 +1 \cdot x^2 = \bm{x^2\cdot (-5x^2+1)}$

Ingatlah bahwa jika faktor persekutuannya identik dengan suatu suku, maka harus ada angka 1 di tempatnya.

Latihan 2

Perhatikan faktor persekutuan dari polinomial berikut:

$\text{A)} \ 8x^2 + 10y^3$

$\text{B)} \ 5x^3-2x^2+4x$

$\text{C)} \ 25x^5+15x^3-20$

$\text{D)} \ 9x^4-3x^3-21x^2-6x$

Lihat solusinya

A) Semua koefisien unsur-unsur penyusun polinomial pertama adalah kelipatan 2, oleh karena itu, dengan mengekstrak faktor persekutuannya, polinomial tersebut menjadi:

$\begin{array}{l} 8x^2 + 10y^3 = \\[2ex] = 2\cdot 4x^2 +2\cdot 5y^3 = \\[2ex] = \bm{2\left(4x^2+5y^3\right)} \end{array}$

B) Dalam semua suku polinomial paling sedikit terdapat satu x, oleh karena itu:

$\begin{array}{l}5x^3-2x^2+4x = \\[2ex] = 5x^2\cdot x-2x\cdot x+4\cdot x= \\[2ex] =\bm{x\left(5x^2-2x+4\right)}\end{array}$

C) Pembagi persekutuan terbesar dari koefisien semua suku polinomial adalah 5, sehingga pembagi persekutuan polinomial tersebut adalah 5:

$\begin{array}{l}25x^5+15x^3-20 = \\[2ex] =5\cdot 5x^5+5\cdot 3x^3-5\cdot 4 = \\[2ex] = \bm{5\left(5x^5+3x^3-4\right)}\end{array}$

D) Semua suku dalam polinomial memiliki paling sedikit satu x dan, terlebih lagi, semua koefisien adalah kelipatan 3. Oleh karena itu, faktor persekutuan polinomial tersebut adalah 3x:

$\begin{array}{l}9x^4-3x^3-21x^2-6x = \\[2ex] = 3x^3\cdot 3x-x^2\cdot 3x-7x\cdot 3x-2\cdot 3x= \\[2ex] = \bm{3x\left(3x^3-x^2-7x-2 \right)}\end{array}$

Latihan 3

Temukan faktor persekutuan dari setiap polinomial berikut dan kurangi:

$\text{A)} \ 4a^2b^5+7a^4b^3-10a^6b^4$

$\text{B)} \ 16x^4y^7z+8x^2y^2z^2+ 24x^3y^5$

$\text{C)} \ 6ab^2c^4-6ab^2c+12a^3b^2c$

$\text{D)} \ 18x^2y+10xy-5xy^3+4z$

Lihat solusinya

A) Semua monomial setidaknya memiliki huruf tersebut

$a$

kuadrat dan huruf

$b$

potong dadu, jadi faktor persekutuannya adalah

$a^2b^3:$

$\begin{array}{l} 4a^2b^5+7a^4b^3-10a^6b^4 = \\[2ex] = 4b^2\cdot a^2b^3+7a^2\cdot a^2b^3-10a^4b\cdot a^2b^3 = \\[2ex] = \bm{a^2b^3\left(4b^2+7a^2-10a^4b\right)} \end{array}$

B) Semua koefisien polinomial adalah kelipatan 8 dan, terlebih lagi, paling sedikit memiliki x ² dan y ² sebagai bagian literal. Oleh karena itu, faktor persekutuan polinomial tersebut adalah 8x ² y ² .

$\begin{array}{l}16x^4y^7z+8x^2y^2z^2+ 24x^3y^5 = \\[2ex] = 2x^2y^5z \cdot 8x^2y^2 +z^2\cdot 8x^2y^2+ 3xy^3\cdot 8x^2y^2= \\[2ex] =\bm{8x^2y^2\left(2x^2y^5z+z^2+3xy^3\right)}\end{array}$

C) Dalam hal ini, faktor persekutuannya bertepatan dengan nilai monomial perantara

$\left(6ab^2c\right)$

, karena koefisien monomial lainnya adalah kelipatan

$6$

dan pasti semua orang pernah mengalaminya

$ab^2c:$

$\begin{array}{l}6ab^2c^4-6ab^2c+12a^3b^2c = \\[2ex] =c^3\cdot 6ab^2c -1\cdot 6ab^2c+2a^2 \cdot 6ab^2c = \\[2ex] = \bm{6ab^2c\left(c^3-1+2a^2\right)}\end{array}$

D) Dalam kasus khusus ini, polinomial tidak memiliki faktor persekutuan, karena tidak ada faktor yang diulang di semua suku polinomial. Oleh karena itu, ekspresi polinomial tidak dapat disederhanakan secara aljabar.

$18x^2y+10xy-5xy^3+4z$

Latihan 4

Sederhanakan pecahan aljabar berikut dengan mengambil faktor persekutuannya:

$\text{A)} \ \cfrac{10x^2+30}{5x-20}$

$\text{B)} \ \cfrac{16x^2-8}{24x-32}$

$\text{C)} \ \cfrac{49x^3+7x}{35x^2-14}$

$\text{D)} \ \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}$

Lihat solusinya

Cara menyederhanakan pecahan aljabar, yaitu pecahan dengan polinomial, adalah dengan mengekstrak faktor persekutuan dari pembilang dan penyebut pecahan tersebut, kemudian menghilangkan faktor yang berulang di atas dan di bawah. di bawah pecahan. JADI:

$\text{A)} \quad \begin{array}{l} \cfrac{10x^2+30}{5x-20}= \cfrac{5\cdot 2x^2 +5\cdot 6}{5\cdot x-5\cdot 4} = \\[4ex] = \cfrac{5(2x^2+6)}{5(x-4)}= \cfrac{\cancel{5}(2x^2+6)}{\cancel{5}(x-4)} = \\[4ex] = \cfrac{\bm{2x^2+6}}{\bm{x-4}} \end{array}$

$\text{B)} \quad \begin{array}{l} \cfrac{16x^2-8}{24x-32} = \cfrac{8 \cdot 2x^2+8 \cdot (-1)}{8 \cdot 3x-8 \cdot 4} =\\[4ex] = \cfrac{8(2x^2-1)}{8(3x-4)}= \cfrac{\cancel{8}(2x^2-1)}{\cancel{8}(3x-4)} =\\[4ex] = \cfrac{\bm{2x^2-1}}{\bm{3x-4}} \end{array}$

$\text{C)} \quad \begin{array}{l}\cfrac{49x^3+7x}{35x^2-14}=\cfrac{7x\cdot 7x^2+7x\cdot 1}{7 \cdot 5x^2+7\cdot (-2)} =\\[4ex] = \cfrac{7x(7x^2+1)}{7(5x^2-2)}= \cfrac{\cancel{7}x(7x^2+1)}{\cancel{7}(5x^2-2)}=\\[4ex] = \cfrac{\bm{x(7x^2+1)}}{\bm{5x^2-2}} \end{array}$

$\text{D)} \quad \begin{array}{l} \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}=\cfrac{4x^2\cdot 2x^2+4x^2\cdot 4x+4x^2\cdot (-1)}{4x\cdot 3x+4x\cdot 5}=\\[4ex] = \cfrac{4x^2(2x^2+4x-1)}{4x(3x+5)}= \cfrac{\cancel{4}x^{\cancel{2}}(2x^2+4x-1)}{\cancel{4}\cancel{x}(3x+5)}=\\[4ex] = \cfrac{\bm{x(2x^2+4x-1)}}{\bm{3x+5}} \end{array}$

Latihan 5

Ambil faktor persekutuan dari ekspresi polinomial berikut:

$\text{A)} \ \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}$

$\text{B)} \ \sqrt{12x^3+16}$

$\text{C)} \ x^2+4x-3x-12$

$\text{D)} \ \cfrac{3}{4}x^2+ \cfrac{1}{2}x-\cfrac{5}{6}$

Lihat solusinya

A) Semua suku polinomial dapat didekomposisi secara faktorial menjadi suku ketiga, oleh karena itu:

$\begin{array}{l} \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}= \\[3ex] = \cfrac{1}{3}\cdot 7x^2+ \cfrac{1}{3}\cdot 8x-\cfrac{1}{3}\cdot 2 = \\[3ex] = \mathbf{\cfrac{1}{3}}\bm{\left(7x^2+8x-2\right)} \end{array}$

B) Faktor persekutuan polinomial di dalam akar adalah 4 tetapi, kemudian, kita dapat mengeluarkan faktor persekutuan tersebut dengan menghitung akar kuadratnya:

$\begin{array}{l}\sqrt{12x^3+16}= \\[2ex] =\sqrt{4\cdot 3x^3+4\cdot 4}= \\[2ex]=\sqrt{4\left(3x^3+4\right)}= \\[2ex] =\bm{2\sqrt{3x^3+4}}\end{array}$

C) Dalam polinomial ini kita dapat menerapkan proses mengekstraksi faktor persekutuan dengan mengelompokkan:

$\begin{array}{l}x^2+4x-3x-12= \\[2ex] =x(x+4)-3(x+4) = \\[2ex] = \bm{(x+4)(x-3)}\end{array}$

D) Semua koefisien pecahan polinomial adalah kelipatan setengah, jadi faktor persekutuan polinomial tersebut adalah ½.

$\begin{array}{l}\displaystyle \frac{3}{4}x^2+ \frac{1}{2}x-\frac{5}{6}= \\[4ex] \displaystyle = \frac{1}{2}\cdot\frac{3}{2}x^2+ \frac{1}{2}\cdot x-\frac{1}{2}\cdot\frac{5}{3}= \\[4ex] \displaystyle = \mathbf{\frac{1}{2}}\bm{\left(}\mathbf{\frac{3}{2}}\bm{x^2+x-}\mathbf{\frac{5}{3}} \bm{\right)}\end{array}$

Bagaimana menurut anda penjelasannya? Apakah kamu menyukainya? Ingatlah juga bahwa jika Anda memiliki pertanyaan tentang cara menentukan faktor persekutuan suatu polinomial atau jika Anda tidak memahami suatu latihan, Anda selalu dapat bertanya kepada kami di komentar, dan kami akan menjawab Anda.

Ekstrak atau hapus faktor persekutuannya

Apa faktor persekutuannya?

Cara mendapatkan (atau mengekstrak) faktor persekutuan

Contoh Pengambilan Faktor Umum (atau Ekstraksi)

Contoh 1

Contoh 2

Contoh 3

Contoh 4

Faktor persekutuan pecahan

Faktor persekutuan dengan mengelompokkan

Latihan faktor umum diselesaikan selangkah demi selangkah

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Tinggalkan Komentar Batalkan Balasan