Di halaman ini Anda akan mengetahui apa itu akar-akar polinomial dan cara menghitungnya. Selain itu, Anda akan dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah pada akar polinomial.
Apa akar-akar polinomial?
Dalam matematika, akar (atau nol) suatu polinomial adalah nilai-nilai yang menghilangkan polinomial tersebut. Artinya, akar-akar suatu polinomial adalah semua nilai yang jika dievaluasi dalam polinomial tersebut, mempunyai nilai numerik sama dengan 0.
Pada akhirnya,
![]()
adalah akar dari polinomial
![]()
Ya
![]()
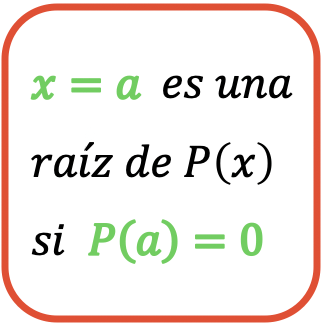
Misalnya, jika kita mempunyai polinomial berikut:
![]()
Kita dapat memverifikasi bahwa salah satu akar polinomial adalah 1, karena nilai numerik polinomial pada x=1 sama dengan nol:
![]()
Sebaliknya, 3 bukan merupakan akar polinomial karena bukan merupakan nilai yang menghilangkan polinomial tersebut, atau dengan kata lain, nilai numerik polinomial pada x=3 berbeda dengan nol:
![]()
Anda mungkin sekarang lebih memahami apa itu akar polinomial, tetapi tidakkah Anda ingin mengetahui berapa banyak akar yang dimiliki suatu polinomial? Atau bagaimana cara mencari semua akar polinomial? Ya, itulah tepatnya yang akan kita lihat di bagian selanjutnya.
Bagaimana cara menghitung semua akar polinomial?
Untuk menemukan semua akar polinomial, Anda harus mengikuti langkah-langkah berikut:
- Pertama, semua pembagi suku bebas polinomial dihitung.
- Kedua, semua nilai yang ditemukan pada langkah sebelumnya dievaluasi dalam polinomial.
- Terakhir, jika ketika mengevaluasi suatu bilangan dalam polinomial, nilai numeriknya sama dengan nol, maka bilangan tersebut adalah akar dari polinomial tersebut. Jika tidak, bilangan tersebut tidak sesuai dengan akar polinomial.
Prosedur ini disimpulkan dari teorema sisa , klik tautan ini untuk mengetahui alasan prosedur khusus ini.
Contoh menghitung akar-akar polinomial
Di bawah ini kita akan menyelesaikan contoh langkah demi langkah agar Anda dapat lebih memahami cara mengambil akar-akar polinomial.
- Berapakah akar-akar polinomial berikut?
![]()
Pertama-tama, kita harus mencari pembagi suku bebas, karena setiap akar polinomial juga merupakan pembagi suku bebas. Jadi, pembagi dari 6 adalah:
Pembagi 6: +1, -1, +2, -2, +3, -3
Ingatlah bahwa jika suatu bilangan merupakan pembagi, maka bilangan negatifnya juga merupakan pembagi. Karena suatu bilangan habis dibagi bilangan positif dan negatif.
Jadi, kemungkinan akar atau nol dari polinomial tersebut adalah: ±1, ±2, ±3. Oleh karena itu, kita perlu menentukan nilai numerik polinomial untuk semua nilai tersebut. Dan, untuk melakukan ini, kita substitusikan nilai-nilai ini ke dalam ekspresi polinomial yang memiliki x:
![]()
![]()
![]()
![]()
![]()
![]()
Jadi polinomialnya hanya hilang jika variabel x bernilai +2 atau +3, jadi berikut akar-akar polinomialnya:
Akar atau nol dari polinomial : +2 dan +3
Di sisi lain, perhatikan bahwa polinomial mempunyai jumlah akar yang sama banyaknya dengan derajatnya, artinya karena polinomial tersebut berderajat kedua, maka polinomial tersebut mempunyai dua akar. Pada sifat-sifat akar suatu polinomial (di bawah), kita akan melihat mengapa karakteristik ini selalu berlaku untuk polinomial mana pun.
Kita baru saja melihat cara mencari akar-akar polinomial. Namun, masih ada cara lain untuk mencapai hal ini, misalnya Anda juga dapat mencari akar polinomial dengan aturan Ruffini. Klik tautan berikut untuk melihat contoh aturan Ruffini , di sini Anda akan menemukan apa saja isi metode terkenal ini dan, juga, apa perbedaan antara kedua prosedur tersebut.
Sifat-sifat akar polinomial
Akar atau nol suatu polinomial mempunyai ciri-ciri sebagai berikut:
- Seperti yang kita lihat sebelumnya, akar bilangan bulat (atau nol) dari suatu polinomial adalah pembagi suku bebas polinomial tersebut.
- Jika kita mengetahui semua akar suatu polinomial, kita dapat menyatakan polinomial tersebut dalam bentuk hasil kali binomial bertipe
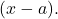
Misalnya polinomial
![]()
Ia memiliki 3 akar yaitu
![]()
Dan
![]()
Oleh karena itu, kita dapat menulis ulang polinomial tersebut dalam bentuk 3 perkalian faktor, yang masing-masing dibentuk oleh variabel
![]()
dan root telah berubah tanda:
![Rendered by QuickLaTeX.com \displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce071610927d2723c8ac2e7b299c1c5d_l3.png)
![]()
Ini disebut pemfaktoran polinomial. Faktanya, salah satu kegunaan utama dalam menentukan akar-akar polinomial adalah digunakan untuk memfaktorkannya. Di tautan berikut Anda dapat mengetahui terdiri dari apa saja operasi khusus ini dan, sebagai tambahan, Anda dapat berlatih dengan latihan faktorisasi polinomial yang terselesaikan .
- Suatu polinomial mempunyai akar sebanyak yang ditunjukkan oleh derajatnya. Jadi, polinomial derajat kedua mempunyai 2 akar, polinomial derajat ketiga mempunyai 3 akar, polinomial derajat keempat mempunyai 4 akar, dan seterusnya.
- Jika suatu polinomial tidak mempunyai suku bebas, berarti salah satu akarnya adalah 0. Maka akar-akar yang lain harus merupakan pembagi koefisien monomial yang berpangkat paling rendah.
Misalnya, polinomial berikut tidak mempunyai suku bebas:
![]()
Jadi salah satu akar polinomial haruslah 0. Dan akar-akar sisanya merupakan pembagi koefisien suku derajat terendah, yaitu -2. Lebih tepatnya, akar lainnya adalah
![]()
Dan
![]()
jadi semua akar polinomialnya adalah:
Akar atau nol dari polinomial: 0, +1 dan -2
- Jika akar-akar suatu polinomial tidak dapat ditentukan, maka polinomial tersebut dikatakan polinomial tak tersederhanakan.
Misalnya kita akan mencoba menghitung akar-akar polinomial berikut:
![]()
Satu-satunya akar polinomial yang mungkin adalah pembagi -1, yaitu -1 dan +1. Oleh karena itu kami mengevaluasi polinomial dengan nilai-nilai berikut:
![]()
![]()
Polinomial tersebut tidak dapat dibatalkan sama sekali, sehingga tidak memiliki akar dan, oleh karena itu, merupakan polinomial yang tidak dapat direduksi.
- Jika polinomial terdiri dari hasil perkalian beberapa polinomial, perkalian ini tidak perlu dilakukan untuk menghitung akar-akarnya, tetapi akar-akar polinomial tersebut adalah akar-akar dari setiap faktor yang dikalikan.
Misalnya, jika kita mempunyai polinomial berikut:
![]()
Dari sifat kedua akar polinomial, kita dapat menyimpulkan bahwa akar polinomial kiri adalah +2 dan akar polinomial kanan adalah -1.
![]()
![]()
Jadi, akar-akar polinomial hasil perkalian kedua faktor tersebut adalah akar-akarnya masing-masing, yaitu +2 dan -1.
![Rendered by QuickLaTeX.com \displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-416399918b5a2a051a6bfc7343ef7960_l3.png)
Latihan soal akar-akar polinomial
Latihan 1
Tentukan jika
![]()
adalah akar dari polinomial berikut:
![]()
Untuk mengetahui apakah
![]()
adalah akar polinomial, kita perlu mengevaluasinya ke nilai tersebut. Belum:
![Rendered by QuickLaTeX.com \begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c88c4456693b0c57d55aba68287414c_l3.png)
Nilai numerik polinomial di
![]()
adalah nol, sehingga secara efektif merupakan akar polinomial.
Latihan 2
Hitung semua akar polinomial berikut:
![]()
Pertama, untuk mencari kemungkinan akar-akar polinomial, kita harus mencari pembagi suku bebasnya. Jadi, pembagi dari 2 adalah:
Pembagi 2: +1, -1, +2, -2
Oleh karena itu, kemungkinan akar atau nol dari polinomial tersebut adalah ±1 dan ±2. Oleh karena itu, kita perlu menghitung berapa polinomial dalam semua nilai ini:
![]()
![]()
![]()
![]()
Jadi, polinomialnya hilang jika x bernilai +1 atau +2, jadi inilah akar-akar polinomialnya:
Akar atau nol dari polinomial : +1 dan +2
Latihan 3
Temukan akar-akar polinomial berikut:
![]()
Pertama-tama kita harus mencari pembagi suku bebas, karena akar suatu polinomial juga merupakan pembagi suku bebas. Jadi, pembagi dari 4 adalah:
Pembagi 4: +1, -1, +2, -2, +4, -4
Oleh karena itu, akar atau nol yang mungkin dari polinomial tersebut adalah ±1, ±2, dan ±4. Oleh karena itu, kita harus mencari nilai numerik polinomial dalam semua nilai berikut:
![]()
![]()
![]()
![]()
![]()
![]()
Jadi, polinomialnya hanya hilang jika x bernilai +1, +2, atau -2, jadi berikut akar-akar polinomialnya:
Akar atau nol dari polinomial : +1, +2 dan -2
Latihan 4
Temukan akar-akar polinomial berikut:
![]()
Dalam hal ini, polinomial tidak mempunyai suku bebas. Oleh karena itu, berdasarkan sifat keempat akar yang dijelaskan di atas, kita mengetahui bahwa salah satu akar polinomial haruslah 0.
Akar polinomial:
![]()
Selanjutnya, dalam hal ini, akar-akar yang mungkin bukanlah pembagi dari suku bebas, melainkan pembagi dari koefisien suku yang derajatnya paling rendah, yaitu 8:
Pembagi 8: +1, -1, +2, -2, +4, -4, +8, -8
Jadi kemungkinan akar atau nol dari polinomial tersebut adalah ±1, ±2, ±4 dan ±8. Oleh karena itu kita harus menghitung nilai numerik polinomial pada semua nilai berikut:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Jadi polinomialnya hilang jika x bernilai +2 atau +4, jadi nilai-nilai tersebut adalah akar-akar polinomialnya. Namun, kita juga perlu menambahkan root 0 yang kita temukan di awal soal. Kesimpulannya, semua akar polinomial adalah:
Akar atau nol dari polinomial : 0, +2 dan +4
Latihan 5
Gunakan sifat-sifat akar polinomial untuk menghitung akar-akar polinomial berikut:
![]()
Seperti yang kita lihat pada sifat akar keenam, ketika polinomial dibentuk oleh produk faktor, tidak perlu menghitung semua akar, karena akar dari seluruh polinomial adalah akar dari setiap faktor.
Selanjutnya dari sifat kedua akar-akar polinomial kita dapat menyimpulkan bahwa akar faktor pertama adalah +1 dan akar faktor kedua adalah -3.
![]()
![]()
Jadi kita hanya perlu mencari akar dari faktor terakhir. Untuk melakukan ini, kita mencari pembagi suku bebas (-2):
Pembagi -2: +1, -1, +2, -2
Jadi kemungkinan akar atau nol dari polinomial terakhir adalah ±1 dan ±2. Dengan mana kita harus menghitung nilai numerik dari polinomial tersebut dalam semua nilai berikut:
![]()
![]()
![]()
![]()
![]()
Oleh karena itu, akar-akar polinomial di sebelah kanan adalah -1 dan 2.
Oleh karena itu, akar-akar seluruh polinomial adalah semua akar-akar yang ditemukan:
Akar atau nol polinomial : +1, -1, +2, -3