Di halaman ini Anda akan mengetahui cara membagi polinomial, baik pembagian polinomial dengan monomial maupun pembagian polinomial dengan polinomial lainnya. Anda juga akan dapat melihat contoh pembagian polinomial dan berlatih dengan latihan penyelesaian langkah demi langkah. Selain itu, Anda akan menemukan properti operasi polinomial ini.
Pembagian polinomial (atau polinomial).
Sebelum kita melihat secara pasti cara pembagian dua polinomial, kita akan mengulas secara singkat konsep pembagian polinomial agar nantinya lebih mudah untuk memahami cara yang akan kita gunakan.
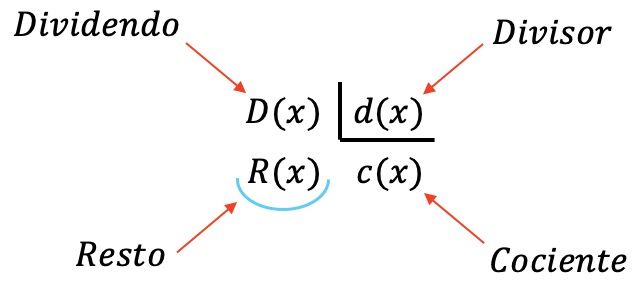
Empat polinomial terlibat dalam pembagian polinomial:
- Dividen : polinomial yang terbagi.
- Pembagi : polinomial yang membagi dividen.
- Hasil bagi : hasil membagi dividen dengan pembaginya.
- Sisa (atau residu): polinomial yang tersisa saat membagi dua polinomial.
Di sisi lain, Anda juga harus mengetahui bahwa ada dua jenis pembagian antar polinomial:
- Pembagian polinomial eksak : pembagian antar polinomial adalah tepat jika sisanya nol. Dalam hal ini, pembagian polinomial sama dengan pembagi dikalikan dengan hasil bagi.
![]()
Apalagi dalam hal ini dividen
![]()
adalah kelipatan dari pembaginya
![]()
dan hasil bagi
![]()
Demikian pula, pembagi polinomial dan hasil bagi polinomial keduanya merupakan pembagi pembagian.
- Pembagian polinomial bilangan bulat : dalam pembagian polinomial bilangan bulat (atau eksak), sisanya bukan nol (0). Kemudian, sifat dasar pembagian polinomial terpenuhi:
![]()
Sekarang kita telah mengetahui apa itu pembagian polinomial, mari kita lihat cara membagi polinomial satu sama lain. Lebih tepatnya akan dijelaskan terlebih dahulu pembagian antara polinomial dan monomial kemudian pembagian antara 2 polinomial.
Pembagian polinomial dengan monomial
Sebelum melihat cara membagi polinomial dengan monomial, mari kita ingat dulu bagaimana monomial dibagi di antara keduanya, karena kita perlu mengetahuinya untuk dapat melakukan operasi polinomial jenis ini.
Pembagian dua monomial melibatkan pembagian koefisien satu sama lain dan bagian literalnya satu sama lain, yaitu koefisien monomial dibagi dan eksponen variabel yang memiliki basis yang sama dikurangi. Lihatlah contoh berikut:
![]()
Sekarang mari kita lihat pembagian polinomial dengan monomial yang melibatkan:
Dalam matematika, untuk menyelesaikan pembagian polinomial dengan monomial, setiap suku polinomial dibagi dengan monomial.
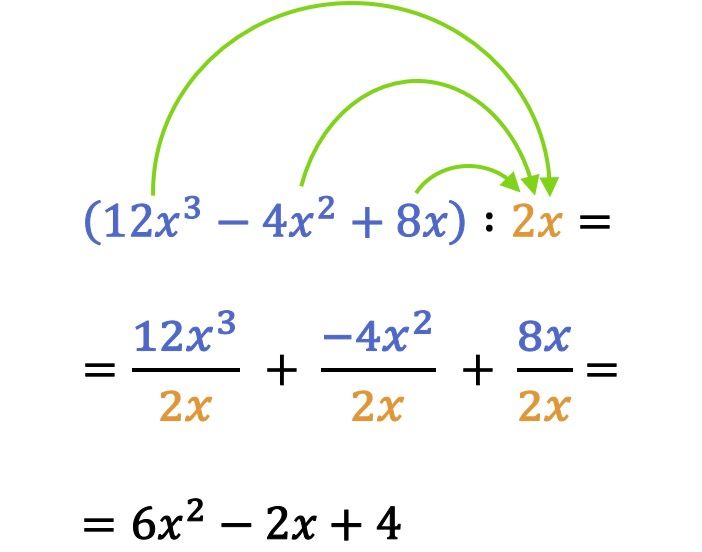
Perhatikan pada contoh pembagian sebelumnya bahwa ketika membagi monomial atau polinomial, Anda juga harus memperhitungkan aturan tanda. Faktanya, kesalahan umum dalam pembagian antara polinomial dan monomial adalah kesalahan tanda suatu suku.
Pembagian suatu polinomial dengan polinomial lainnya
Untuk membagi dua polinomial, Anda harus mengikuti prosedurnya, jadi mari kita lihat seperti apa cara membagi polinomial, yang juga disebut pembagian panjang polinomial, dengan menyelesaikan contoh langkah demi langkah:
- Hitung hasil pembagian polinomial

antara polinomial
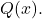
Menjadi dua polinomial:
![]()
![]()
Hal pertama yang harus dilakukan adalah memasukkan polinomial ke dalam bentuk pembagian. Di sebelah kiri kita tulis pembilang pecahan (polinomial pembagi) dan di sebelah kanan kita tulis penyebut pecahan (polinomial pembagi):
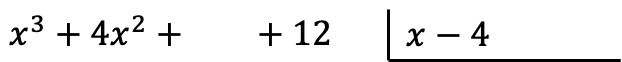
Peringatan: Jika suatu polinomial tidak memiliki monomial dengan derajat tertentu, kita harus menyisakan spasi pada tempatnya. Misalnya polinomial
![]()
Tidak ada semester tahun pertama, jadi ada ruang kosong saja.
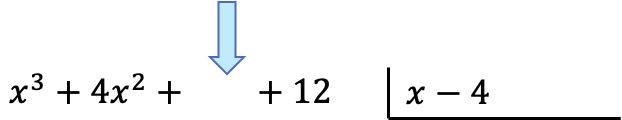
Setelah kita memiliki polinomial, kita akan mencari hasil bagi. Dan untuk mencari suku pertama hasil bagi kita harus membagi suku pertama pembagian dengan suku pertama pembagi:
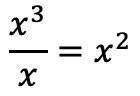
Dan kami menempatkan hasil pembagian sebagai ganti hasil bagi:
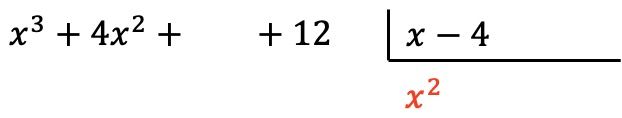
Sekarang kita mengalikan suku yang ditemukan oleh setiap elemen pembagi, dan kita menempatkan setiap hasil di bawah pembagian pada kolom yang sesuai , dengan mengubah tandanya :
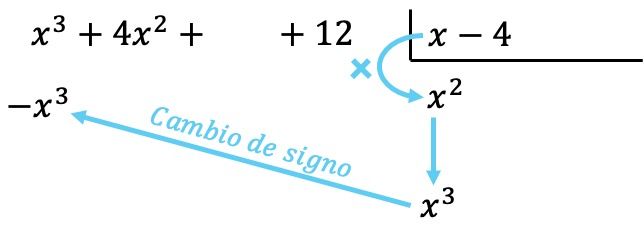
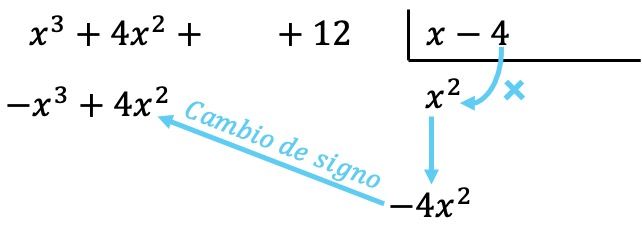
Seperti dalam semua operasi polinomial, penting untuk mengurutkan polinomial dari derajat tertinggi ke derajat terendah sehingga semua suku dengan derajat yang sama berada di kolom yang sama.
Setelah kita menempatkan hasil perkalian dengan tanda berlawanan, kita perlu menjumlahkan suku-suku yang disejajarkan secara vertikal:
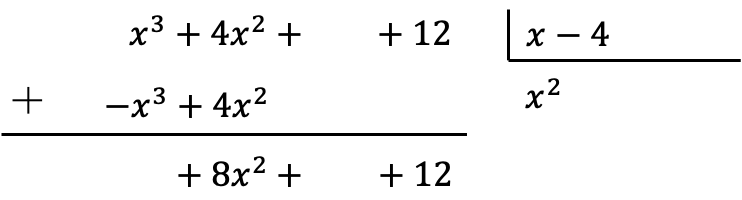
Perhatikan bahwa dengan melakukan penjumlahan ini, koefisien dengan derajat tertinggi akan hilang dan, oleh karena itu, kita memiliki suku yang lebih sedikit dalam dividen.
Sekarang kita perlu mengulangi prosedur yang sama hingga pembagian polinomialnya satu derajat lebih kecil dari pembagi polinomialnya.
Oleh karena itu, suku pertama dividen dibagi dengan suku pertama pembagi:
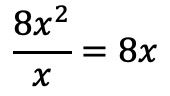
Kami menempatkan hasilnya dalam hasil bagi:
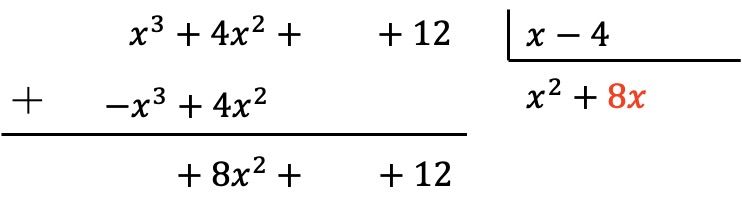
Seperti sebelumnya, kita mengalikan suku baru dari hasil bagi dengan setiap elemen pembagi dan kita memasukkan hasil yang berlawanan tanda pada kolom yang sesuai dari pembagi:
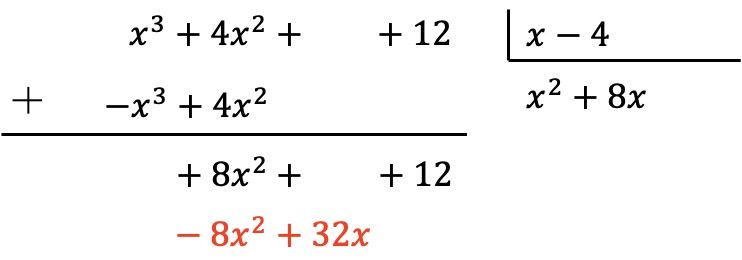
Dan kami menambahkan secara vertikal:
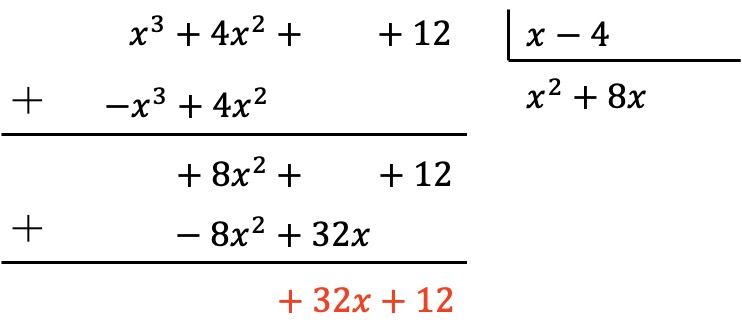
Polinomial pembagi masih tidak kurang satu derajat dari polinomial pembagi, jadi kita perlu terus melakukan proses yang sama.
Jadi, pertama-tama kita membagi suku pertama pembagi dengan suku pertama pembagi, kemudian kita mengalikan hasilnya dengan masing-masing suku pembagi, lalu kita memberi tanda pada hasil modifikasi tersebut di dalam pembagi, dan terakhir, kita menjumlahkan secara vertikal:
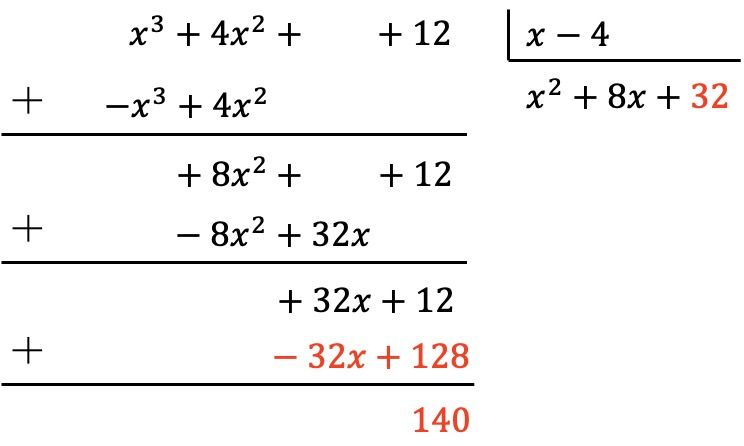
Jadi kita telah memperoleh bahwa polinomial dari pembaginya berderajat lebih kecil dari derajat pembaginya, karena pembaginya berderajat 0 dan pembaginya berderajat 1. Oleh karena itu, pembagiannya selesai.
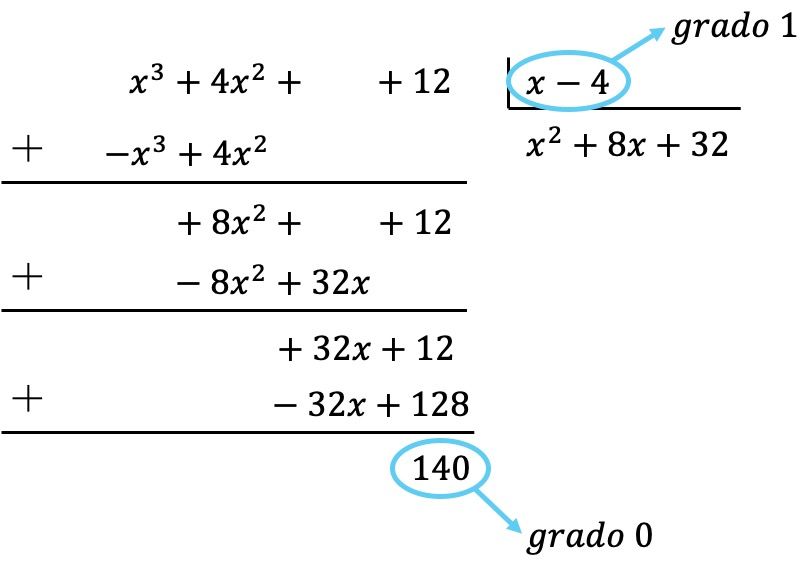
Maka hasil pembagiannya adalah:
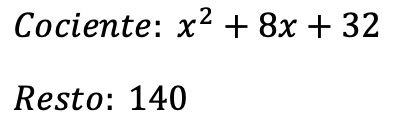
Di sisi lain, kita dapat memverifikasi bahwa kita telah melakukan pembagian polinomial dengan benar berdasarkan kondisi dasar pembagian polinomial:
![]()
![]()
![]()
![]()
✅
Persamaannya terpenuhi, sehingga pembagian polinomial dilakukan dengan benar.
Setelah kita selesai membagi polinomial, semoga penjelasan ini dapat membantu anda. Apa pendapat Anda tentang metode pembagian polinomial? Apakah Anda ragu? Apakah kamu menyukainya? Atau apakah Anda lebih suka pembagian polinomial tidak ada? 😂 Kami membaca Anda di komentar! 👇👇👇
Sifat-sifat membagi polinomial
Setiap pembagian polinomial memenuhi ciri-ciri berikut:
✓ Derajat pembagian polinomial harus selalu lebih besar dari derajat pembagi polinomial.
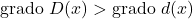 ✓ Derajat pembagian polinomial sama dengan jumlah derajat pembagi dan hasil bagi.
✓ Derajat pembagian polinomial sama dengan jumlah derajat pembagi dan hasil bagi.
![]()
✓ Derajat sisanya selalu lebih kecil dari derajat pembaginya (dan juga pembaginya).
![]()
✓ Dividen sama dengan hasil kali pembagi dikalikan hasil bagi ditambah sisanya. Kondisi ini juga berlaku pada pembagian angka.
![]()
Latihan soal pembagian polinomial
Latihan 1
Tentukan hasil pembagian polinomial dengan monomial berikut:
![]()
Untuk membagi polinomial dengan monomial, Anda harus menyelesaikan pembagian setiap suku polinomial dengan monomial tersebut:
![Rendered by QuickLaTeX.com \begin{aligned} \left(15x^5+9x^3 \right) : \left(3x^2\right) & = \cfrac{15x^{5}}{3x^2}+ \cfrac{9x^3}{3x^2} \\[2ex] & = \bm{5x^3+3x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffa558b26adc36e2ac45a842a6cf33df_l3.png)
Ingatlah bahwa ketika membagi monomial, koefisiennya dibagi satu sama lain dan eksponen pangkat yang basisnya sama dikurangi.
Latihan 2
Hitung pembagian polinomial dengan monomial berikut:
![]()
Untuk membagi polinomial dengan monomial, Anda harus membagi setiap suku polinomial dengan monomial tersebut:
![Rendered by QuickLaTeX.com \begin{aligned} \left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right) & = \cfrac{16x^5}{4x^2}+ \cfrac{-4x^3}{4x^2} + \cfrac{-20x^2}{4x^2} \\[2ex] & = \bm{4x^3-x-5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-868da1546d3e4d33e8226774020cbb2d_l3.png)
Ingatlah bahwa dalam pembagian monomial, koefisien dibagi satu sama lain dan eksponen pangkat dengan basis ekuivalen dikurangi.
Latihan 3
Selesaikan pembagian polinomial dengan monomial berikut:
![]()
Untuk membagi polinomial dengan monomial, Anda harus menyelesaikan pembagian setiap suku polinomial dengan monomial tersebut:
![Rendered by QuickLaTeX.com \begin{aligned} \left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right) & = \cfrac{12x^{10}}{-6x^3}+ \cfrac{-30x^{7}}{-6x^3} + \cfrac{-18x^6}{-6x^3} + \cfrac{54x^4}{-6x^3} \\[2ex] & = \bm{-2x^7+5x^4+3x^3-9x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a8d5fe46b397f2f531a865e7cb0df3cf_l3.png)
Ingatlah bahwa monomial pembagi adalah negatif dan oleh karena itu tanda-tanda semua pembagian berubah.
Latihan 4
Lakukan pembagian polinomial berikut:
![]()
Untuk membagi polinomial Anda harus menerapkan cara yang dijelaskan di atas:
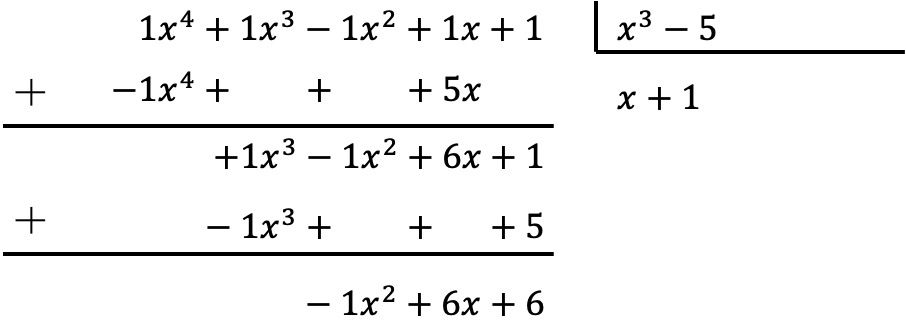
Oleh karena itu, hasil pembagian kedua polinomial tersebut adalah:
Hasil bagi:
![]()
Istirahat:
![]()
Latihan 5
Hitung pembagian polinomial berikut:
![]()
Untuk menyelesaikan pembagian polinomial dengan binomial kita harus menerapkan metode yang kita lihat di atas:
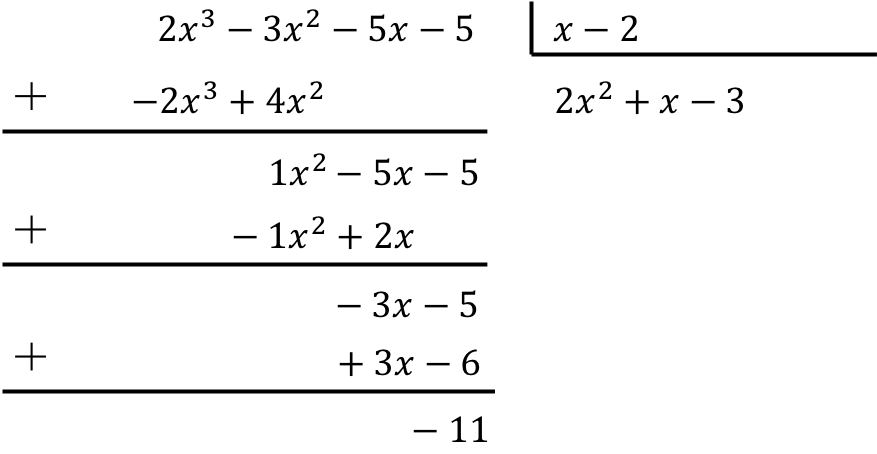
Oleh karena itu, hasil pembagian polinomial adalah:
Hasil bagi:
![]()
Istirahat:
![]()
Latihan 6
Selesaikan pembagian polinomial berikut:
![]()
Untuk menghitung pembagian polinomial, kita harus menerapkan metode yang dijelaskan:
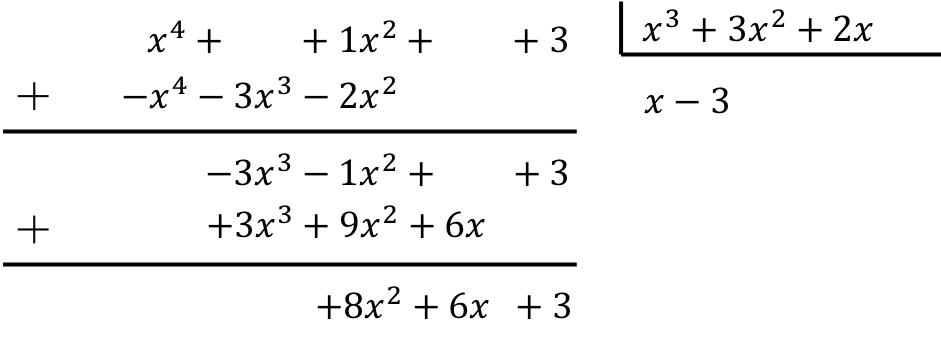
Oleh karena itu, hasil pembagian kedua polinomial tersebut adalah:
Hasil bagi:
![]()
Istirahat:
![]()
Latihan 7
Temukan hasil pembagian antara 2 polinomial berikut:
![]()
Untuk menghitung pembagian polinomial dengan trinomial Anda harus menerapkan metode yang dijelaskan:
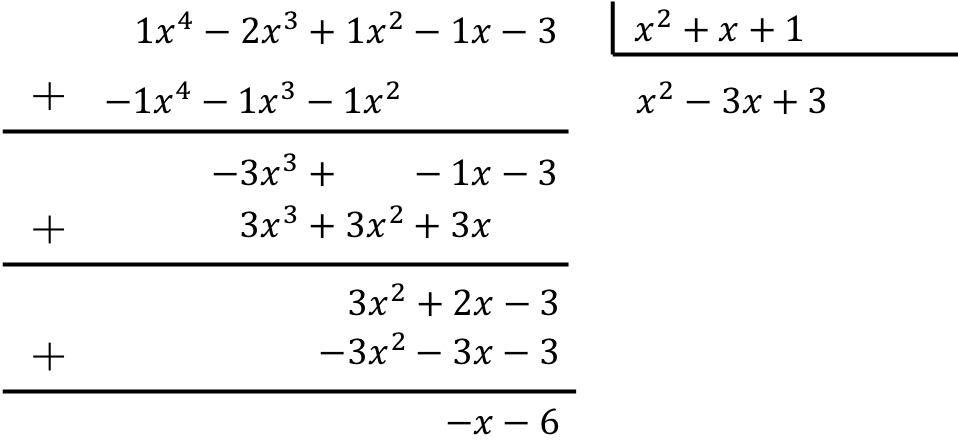
Oleh karena itu, hasil pembagian kedua polinomial tersebut adalah:
Hasil bagi:
![]()
Istirahat:
![]()
👉👉👉Jika Anda sudah sampai sejauh ini, berarti Anda sudah mengetahui cara pembagian polinomial. Terang! Sekarang setelah Anda menguasai pembagian polinomial, ketahuilah bahwa ada metode yang memungkinkan Anda menyelesaikan pembagian tertentu antar polinomial dengan lebih cepat . Ini adalah pembagian sintetis atau aturan Ruffini , Anda dapat melihat bagaimana trik ini diterapkan dan kapan dapat digunakan dengan mengklik link.😉