Pada artikel ini kita akan melihat cara merepresentasikan semua jenis fungsi pada grafik. Selain itu, Anda akan menemukan latihan langkah demi langkah yang diselesaikan dalam merepresentasikan fungsi pada grafik.
Cara merepresentasikan suatu fungsi pada grafik
Untuk merepresentasikan suatu fungsi pada grafik, langkah-langkah berikut harus dilakukan:
- Temukan domain dari fungsi tersebut.
- Hitung titik potong fungsi tersebut dengan sumbu kartesius.
- Hitung asimtot fungsi tersebut.
- Pelajari monotonisitas suatu fungsi dan temukan titik ekstrem relatifnya .
- Pelajari kelengkungan fungsi tersebut dan temukan titik beloknya .
- Plot titik potong, asimtot, ekstrem relatif, dan titik belok, lalu plot fungsinya.
Contoh merepresentasikan suatu fungsi
Agar Anda dapat melihat bagaimana suatu fungsi direpresentasikan secara grafis, kita akan menyelesaikan latihan berikut langkah demi langkah:
- Gambarkan fungsi rasional berikut pada grafik:
![]()
Hal pertama yang harus dilakukan adalah menghitung domain fungsi tersebut . Ini adalah fungsi rasional, jadi kita perlu menyetel penyebutnya sama dengan nol untuk melihat bilangan mana yang tidak termasuk dalam domain fungsi tersebut:
![]()
![]()
Jadi, jika x sama dengan 1, penyebutnya adalah 0 sehingga fungsinya tidak ada. Oleh karena itu, domain fungsi tersebut terdiri dari semua bilangan real kecuali x=1.
![]()
Untuk mencari titik potong dengan sumbu X , kita harus menyelesaikan persamaannya
![]()
Karena fungsi selalu bernilai 0 pada sumbu X:
![]()
![]()
Syarat
![]()
Caranya adalah dengan membagi seluruh ruas kiri, sehingga kita dapat mengalikannya dengan seluruh ruas kanan:
![]()
![]()
![]()
Maka titik potongnya dengan sumbu OX adalah:
![]()
Dan untuk mencari titik potong dengan sumbu Y , kita hitung
![]()
Karena x selalu 0 pada sumbu Y:
![]()
Oleh karena itu, titik potong dengan sumbu OY adalah:
![]()
Dalam hal ini, ketika fungsi melewati titik asal koordinat, titik potong dengan sumbu X bertepatan dengan titik potong dengan sumbu Y.
Setelah kita mengetahui domain dan titik potongnya, kita perlu menghitung asimtot fungsinya .
Untuk melihat apakah suatu fungsi mempunyai asimtot vertikal, kita perlu menghitung limit fungsi tersebut di titik-titik yang tidak termasuk dalam domain (dalam hal ini x=1). Dan jika hasilnya tak terhingga, maka itu adalah asimtot vertikal. Belum:
![]()
Karena limit fungsi ketika x cenderung 1 menghasilkan tak terhingga, x=1 adalah asimtot vertikal:
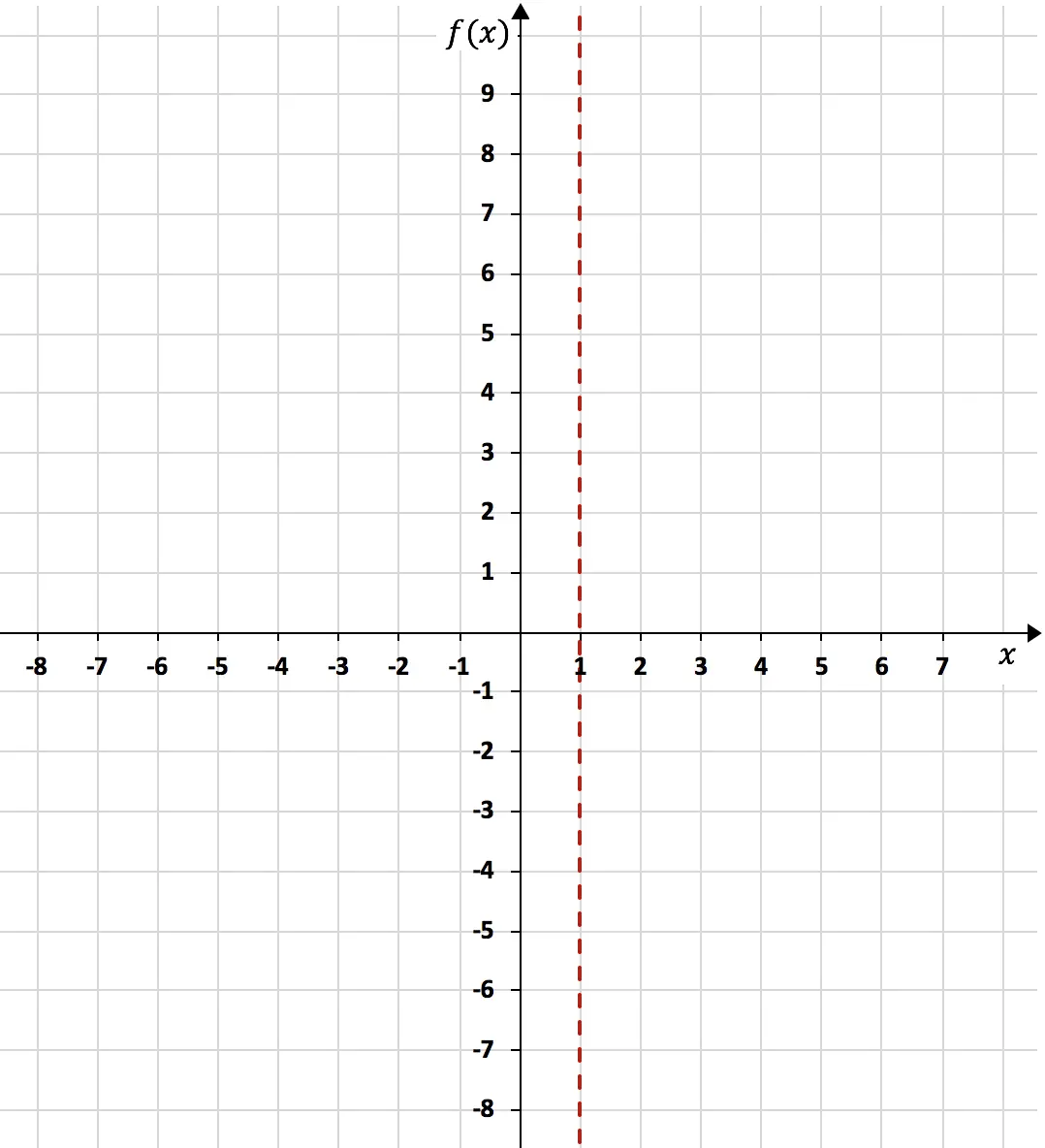
Setelah asimtot vertikal dihitung, perlu dihitung batas lateral fungsi terhadap asimtot tersebut. Karena kita tidak tahu apakah fungsinya akan cenderung -∞ atau +∞ ketika mendekati x=1 dari kiri, dan kita tidak tahu kapan mendekati x=1 dari kanan.
Jadi, kita lanjutkan menghitung limit lateral kiri fungsi tersebut di x=1:
![]()
Untuk menghitung batas lateral suatu titik secara numerik, kita harus mensubstitusi suatu bilangan ke dalam fungsi yang sangat dekat dengan titik tersebut. Dalam hal ini, kita menginginkan angka yang sangat dekat dengan 1 di sebelah kiri, misalnya 0,9. Oleh karena itu, kita substitusikan titik 0,9 ke dalam fungsi:
![]()
Batas lateral asimtot hanya dapat menghasilkan +∞ atau -∞. Dan dengan mensubstitusi angka yang sangat dekat dengan 1 di sebelah kiri ke dalam fungsi tersebut, kita memperoleh hasil negatif, limit di sebelah kiri adalah -∞:
![]()
Sekarang kita melakukan prosedur yang sama dengan batas sisi kanan:
![]()
Kami mengganti angka yang sangat dekat dengan 1 di sebelah kanan ke dalam fungsi tersebut. Misalnya poin 1.1:
![]()
Dalam hal ini hasil batas sisinya adalah bilangan positif. Oleh karena itu, limit di sebelah kanan adalah +∞:
![]()
Kesimpulannya, pada x=1 fungsinya cenderung ke arah minus tak terhingga di sebelah kiri, dan ditambah tak terhingga di sebelah kanan:
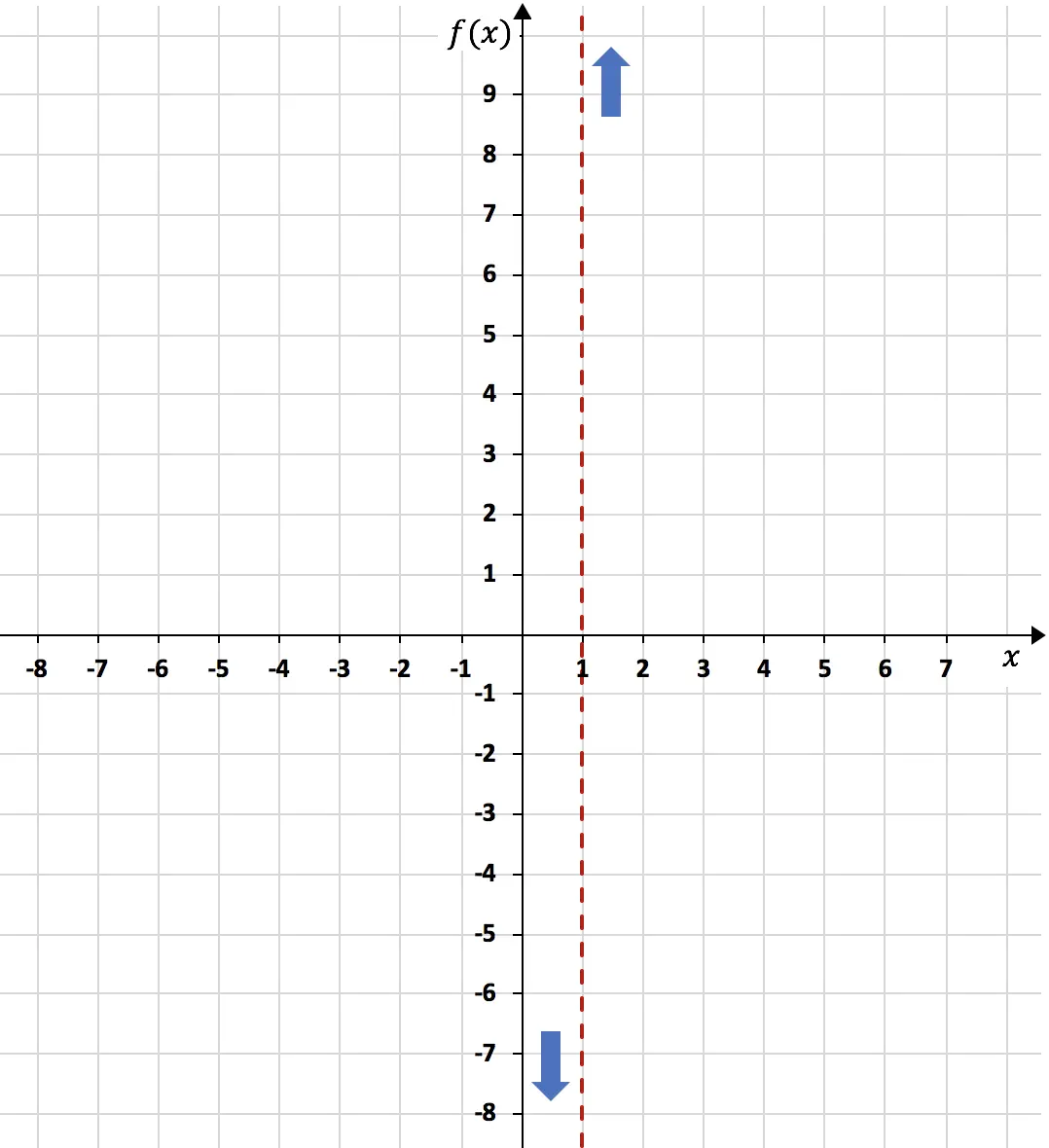
Sebaliknya, asimtot horizontal suatu fungsi adalah hasil dari limit fungsi tersebut. Belum:
![]()
Ingat cara menghitung batas tak hingga dari fungsi rasional:
![\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”></p>
</p>
</div>
<p> Limit tak terhingga dari fungsi tersebut menghasilkan +∞, sehingga fungsi tersebut tidak memiliki asimtot horizontal.</p>
<p> Kami sekarang menghitung asimtot miring. Asimtot miring berbentuk</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c969e4b99985b44006e57d554ff0247_l3.png)
![]()
. DAN
![]()
Itu dihitung dengan rumus berikut:
![]()
![]()
X seolah-olah memiliki angka 1 sebagai penyebutnya:
![]()
Ini adalah pembagian pecahan, jadi kita mengalikannya secara melintang:
![]()
![]()
Dan kami menghitung batasnya:
![]()
Jadi m=1. Sekarang kita menghitung
![]()
dengan rumus berikut:
![]()
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty](https://mathority.org/wp-content/ql-cache/quicklatex.com-10dfa8fdcfbf0c978e02374654a66b7d_l3.png)
Tapi kita mendapatkan ketidakterbatasan tak terhingga dikurangi tak terhingga, jadi kita harus mereduksi suku-suku tersebut menjadi penyebut yang sama. Untuk melakukannya, kita mengalikan dan membagi suku x dengan penyebut pecahan:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-70026c2aed1bb58a120f8c18423d9ef5_l3.png)
Karena kedua suku tersebut memiliki penyebut yang sama, kita dapat mengelompokkannya:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-7702287a02af6d8e3dddaa3f0c6eb1b5_l3.png)
Dan akhirnya kami memecahkan batasnya:
![Rendered by QuickLaTeX.com \displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-feb5faa9dc5d3b68d3273ad4d75d2bb1_l3.png)
Jadi n = 1. Oleh karena itu, asimtot miringnya adalah:
![]()
![]()
![]()
Setelah kami menghitung asimtot miring, kami merepresentasikannya pada grafik yang sama dengan membuat tabel nilai:
![]()

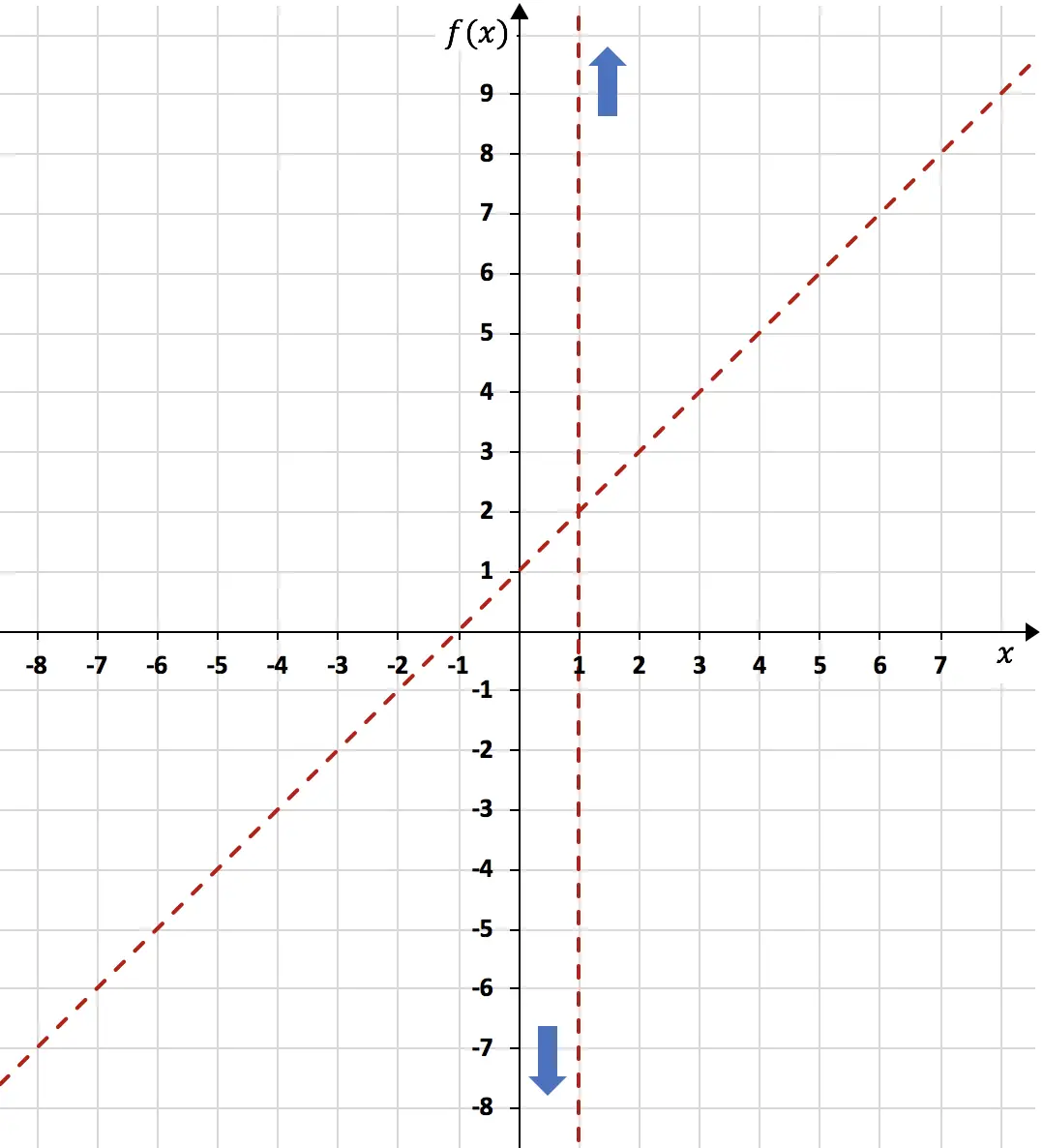
Sekarang setelah kita mengetahui semua asimtot suatu fungsi, kita perlu menganalisis monotonisitas fungsi tersebut . Artinya, kita perlu mempelajari pada interval mana fungsi tersebut meningkat dan pada interval mana fungsi tersebut menurun. Oleh karena itu kami menghitung turunan pertama dari fungsi tersebut:
![]()
![]()
Dan sekarang kita menetapkan turunannya sama dengan 0 dan menyelesaikan persamaannya:
![]()
![]()
Syarat
![]()
Caranya adalah dengan membagi seluruh ruas kiri, sehingga kita dapat mengalikannya dengan seluruh ruas kanan:
![]()
![]()
Kami mengekstrak faktor persekutuan untuk menyelesaikan persamaan kuadrat:
![]()
Agar perkaliannya sama dengan 0, salah satu dari dua unsur perkaliannya harus nol. Oleh karena itu, kami menetapkan setiap faktor sama dengan 0 dan memperoleh kedua solusi persamaan:
![Rendered by QuickLaTeX.com \displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55127e675ce8f7742db17d565c2ae507_l3.png)
Sekarang kita nyatakan pada garis bilangan semua titik kritis yang ditemukan, yaitu titik-titik yang tidak termasuk dalam domain (x=1) dan titik-titik yang membatalkan turunan (x=0 dan x=2):

Dan kita evaluasi tanda turunannya pada setiap interval, untuk mengetahui apakah fungsinya naik atau turun. Oleh karena itu, kita mengambil sebuah titik di setiap interval (tidak pernah titik kritisnya) dan melihat tanda apa yang dimiliki turunannya pada titik tersebut:
![]()
![]()
![]()
![]()
![]()
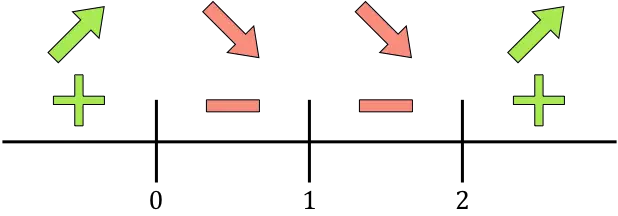
Jika turunannya positif berarti fungsinya meningkat, dan jika turunannya negatif berarti fungsinya menurun. Oleh karena itu, interval pertumbuhan dan penurunannya adalah:
Pertumbuhan:
![]()
Mengurangi:
![]()
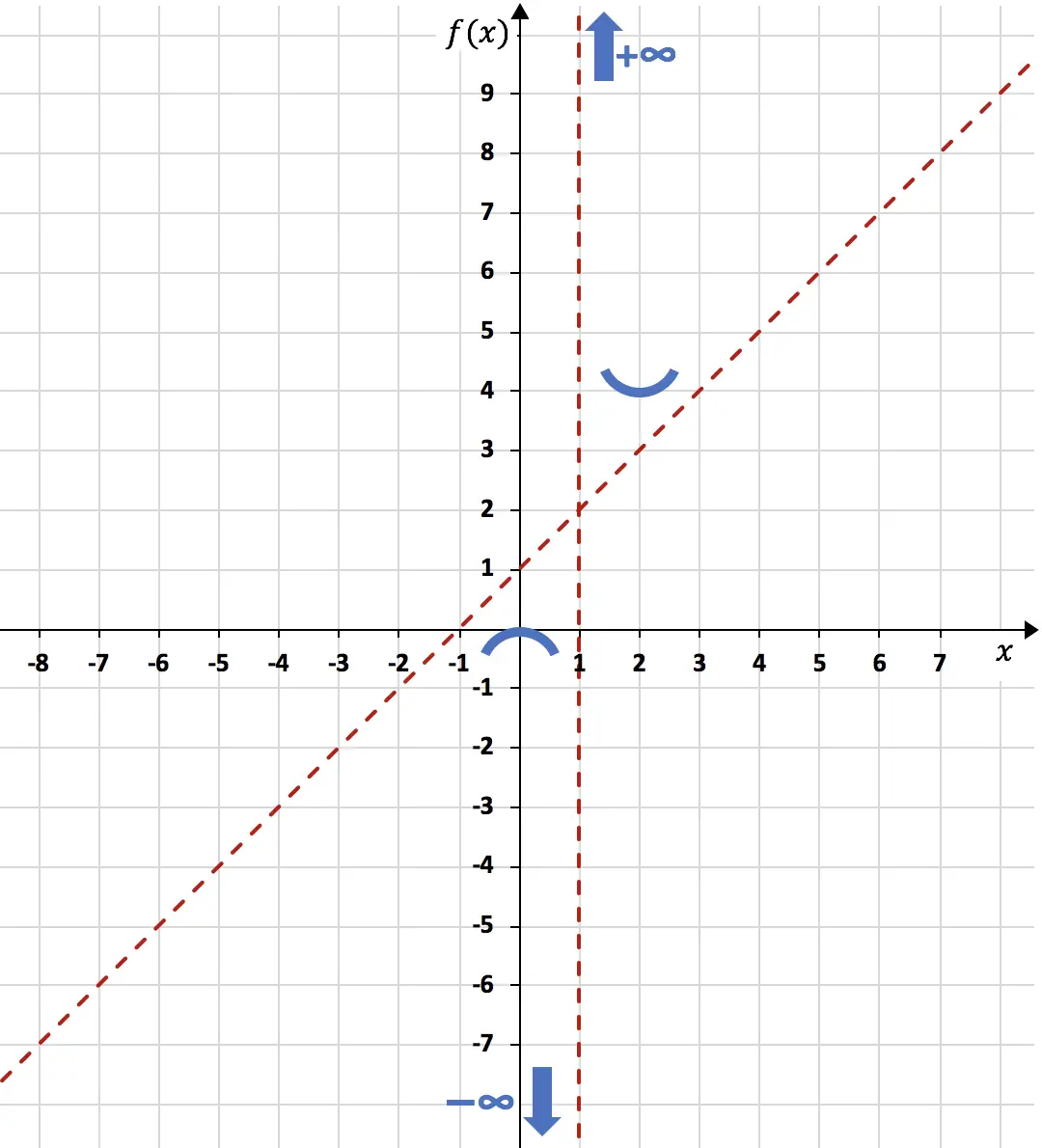
Selanjutnya, pada x=0 fungsinya berubah dari naik ke turun, jadi x=0 adalah maksimum relatif dari fungsi tersebut. Dan pada x=2, fungsinya berubah dari menurun menjadi meningkat, jadi x=2 adalah minimum relatif dari fungsi tersebut.
Terakhir, kita substitusikan nilai ekstrem yang ditemukan ke dalam fungsi asli untuk mencari koordinat Y dari titik-titik tersebut:
![]()
![]()
Oleh karena itu, ekstrem relatif dari fungsi tersebut adalah:
Maksimal tepat sasaran
![]()
Minimal untuk menunjuk
![]()
Kami mewakili maksimum dan minimum pada grafik:
Terakhir, cukup mempelajari kelengkungan fungsi , yaitu mempelajari interval kecekungan dan kecembungan fungsi. Untuk melakukan ini, kami menghitung turunan keduanya:
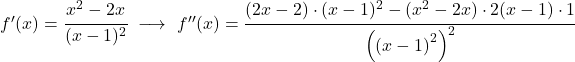
![]()
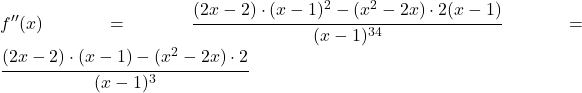
![]()
![]()
Dan sekarang kita menetapkan turunan kedua sama dengan nol dan menyelesaikan persamaan:
![]()
![]()
![]()
![]()
2 tidak akan pernah sama dengan 0, begitulah persamaannya
![]()
Tidak ada solusi.
Sekarang kita nyatakan pada garis bilangan semua titik kritis yang ditemukan, yaitu titik-titik yang tidak termasuk dalam domain (x=1) dan titik-titik yang menghilangkan turunan kedua (dalam hal ini tidak ada satupun yang tidak):

Dan kita evaluasi tanda turunannya pada setiap interval, untuk mengetahui apakah fungsinya cembung atau cekung. Oleh karena itu, kita mengambil sebuah titik di setiap interval (bukan titik tunggalnya) dan melihat tanda apa yang dimiliki turunannya pada titik tersebut:
![]()
![]()
![]()

Dan akhirnya kita menyimpulkan interval kecekungan dan kecembungan fungsi tersebut. Jika turunan keduanya positif berarti fungsinya cembung.
![]()
, dan jika turunan keduanya negatif berarti fungsinya cekung
![]()
. Oleh karena itu, interval kecekungan dan kecembungan adalah:
Cembung
![]()
:
![]()
Cekung
![]()
:
![]()
Namun meskipun terjadi perubahan kelengkungan pada x=1, hal tersebut bukanlah titik belok. Karena x=1 bukan milik domain fungsi tersebut.
Jadi kita bisa menyelesaikan representasi fungsi menggunakan semua yang kita hitung:
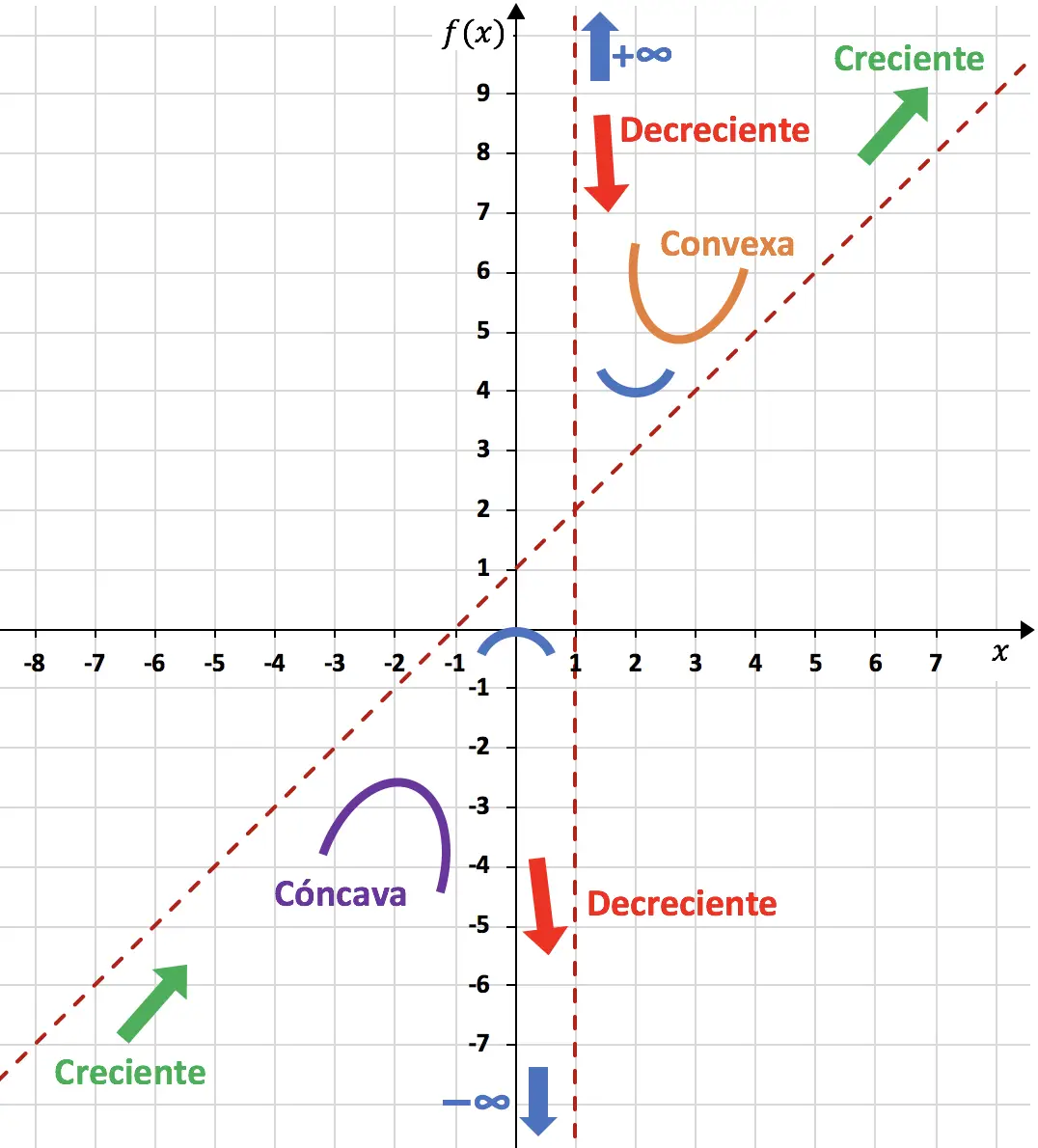
Oleh karena itu, fungsi yang direpresentasikan pada grafik terlihat seperti ini:
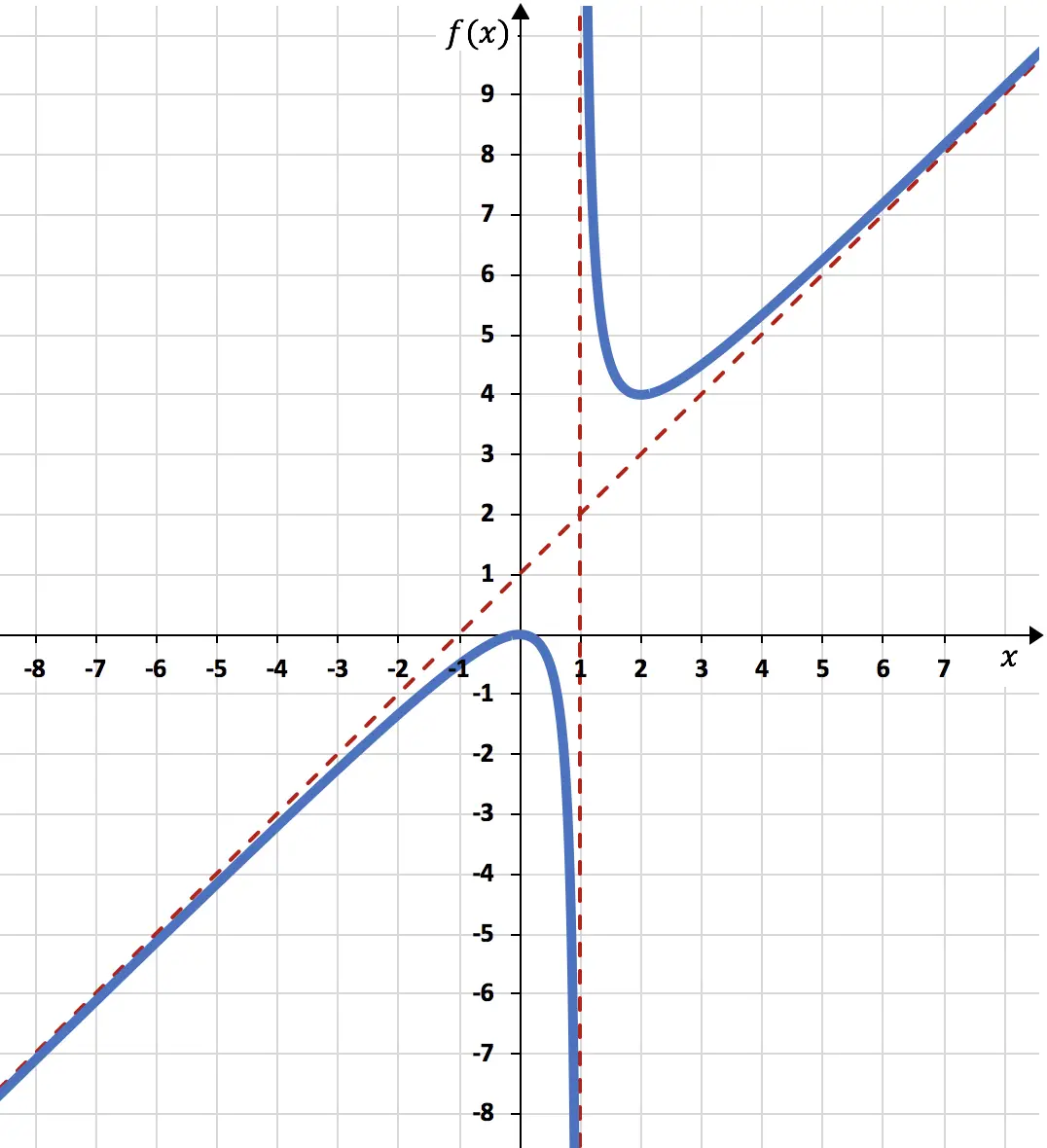
Latihan yang diselesaikan untuk merepresentasikan fungsi
Latihan 1
Gambarkan fungsi polinomial berikut:
![]()
Hal pertama yang harus dilakukan adalah menghitung domain definisi fungsi. Ini adalah fungsi polinomial, jadi domainnya hanya terdiri dari bilangan real:
![]()
Untuk mencari titik potong dengan sumbu X, kita selesaikan
![]()
![]()
![]()
Ini adalah persamaan derajat yang lebih besar dari 2. Oleh karena itu, kita memfaktorkan persamaan tersebut:
![]()
Jadi x=-1 adalah penyelesaian. Dan kami menghitung solusi lainnya dengan menyelesaikan persamaan kuadrat yang dihasilkan:
![Rendered by QuickLaTeX.com \begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e79a2a2f6650c4095c0dca52188c40c3_l3.png)
Maka titik potongnya terhadap sumbu X adalah:
![]()
Dan
![]()
Dan untuk mencari titik potong dengan sumbu Y, kita hitung
![]()
Karena x selalu 0 pada sumbu Y:
![]()
Maka titik potongnya dengan sumbu Y adalah:
![]()
Untuk melihat apakah suatu fungsi mempunyai asimtot vertikal, kita perlu menghitung limit fungsi tersebut di titik-titik yang tidak termasuk dalam domain tersebut. Dalam hal ini, domain mencakup semua bilangan real. Oleh karena itu, fungsi tersebut tidak memiliki asimtot vertikal.
Sebaliknya, asimtot horizontal suatu fungsi adalah hasil dari limit fungsi tersebut. Belum:
![]()
Limit tak terhingga dari fungsi tersebut menghasilkan +∞, sehingga fungsi tersebut tidak memiliki asimtot horizontal.
Kami sekarang menghitung asimtot miring. Asimtot miring berbentuk
![]()
DAN
![]()
Itu dihitung dengan rumus berikut:
![]()
![]()
Batasnya memberi kita +∞, jadi fungsinya juga tidak memiliki asimtot miring.
Untuk mempelajari monotonisitas suatu fungsi, pertama-tama kita harus menghitung turunannya:
![]()
Sekarang kita atur turunannya sama dengan 0 dan selesaikan persamaannya:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d23e2b378508baca9f51117fc8767e90_l3.png)
Sekarang kita nyatakan pada garis bilangan semua titik tunggal yang diperoleh, yaitu titik-titik yang tidak termasuk dalam domain (dalam hal ini, semuanya termasuk) dan titik-titik yang membatalkan turunan (x=0 dan x =2) :

Dan kita evaluasi tanda turunannya pada setiap interval, untuk mengetahui apakah fungsinya naik atau turun. Oleh karena itu, kita mengambil sebuah titik di setiap interval (bukan titik tunggalnya) dan melihat tanda apa yang dimiliki turunannya pada titik tersebut:
![]()
![]()
![]()

Jika turunannya positif berarti fungsinya meningkat, dan jika turunannya negatif berarti fungsinya menurun. Oleh karena itu, interval pertumbuhan dan penurunannya adalah:
Pertumbuhan:
![]()
Mengurangi:
![]()
Fungsi tersebut berubah dari naik ke turun pada x=0, jadi x=0 adalah maksimum dari fungsi tersebut. Dan fungsinya berubah dari menurun menjadi meningkat pada x=2, jadi x=2 adalah minimum dari fungsi tersebut.
Terakhir, kita substitusikan nilai ekstrem yang ditemukan ke dalam fungsi asli untuk mencari koordinat Y dari titik-titik tersebut:
![]()
![]()
Oleh karena itu, ekstrem relatif dari fungsi tersebut adalah:
Maksimal tepat sasaran
![]()
Minimal untuk menunjuk
![]()
Untuk mempelajari kelengkungan suatu fungsi, kita menghitung turunan keduanya:
![]()
Sekarang kita atur turunan keduanya sama dengan 0 dan selesaikan persamaannya:
![]()
![]()
![]()
![]()
Kami menyatakan pada garis semua titik tunggal yang ditemukan, yaitu titik-titik yang tidak termasuk dalam domain (dalam hal ini semuanya termasuk) dan titik-titik yang membatalkan turunan (x=1):

Dan sekarang kita evaluasi tanda turunan keduanya pada setiap interval, untuk mengetahui apakah fungsinya cekung atau cembung. Oleh karena itu, kita mengambil sebuah titik di setiap interval (tidak pernah berupa titik tunggal) dan melihat tanda apa yang dimiliki turunan kedua pada titik tersebut:
![]()
![]()

Jika turunan keduanya positif berarti fungsinya cembung.
![]()
, dan jika turunan keduanya negatif berarti fungsinya cekung
![]()
. Oleh karena itu, interval kecekungan dan kecembungan adalah:
Cembung
![]()
:
![]()
Cekung
![]()
:
![]()
Selain itu, fungsi berubah dari cekung menjadi cembung pada x=1, jadi x=1 adalah titik belok fungsi tersebut.
Terakhir, kita substitusikan titik belok yang ditemukan ke dalam fungsi asli untuk mencari koordinat Y dari titik tersebut:
![]()
Oleh karena itu, titik balik dari fungsi tersebut adalah:
Titik balik:
![]()
Terakhir, berdasarkan semua informasi yang telah kami hitung, kami membuat grafik fungsinya:
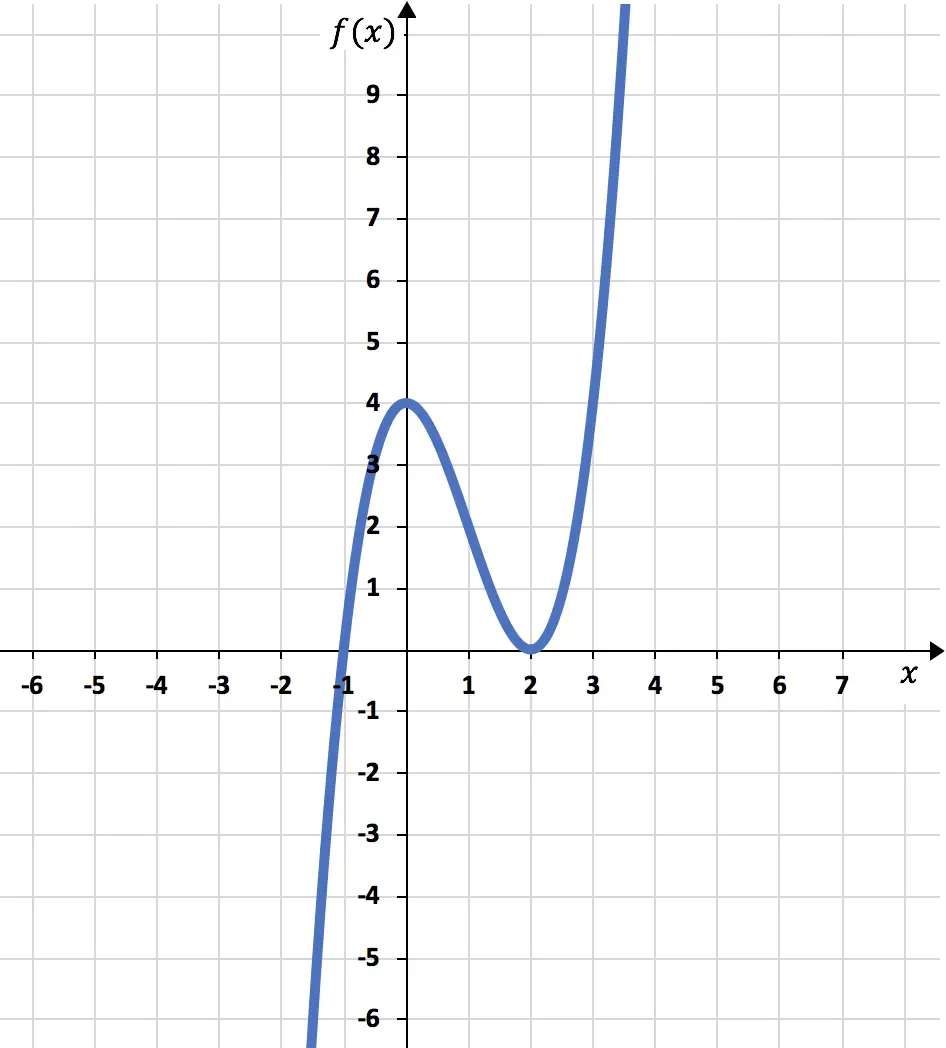
Latihan 2
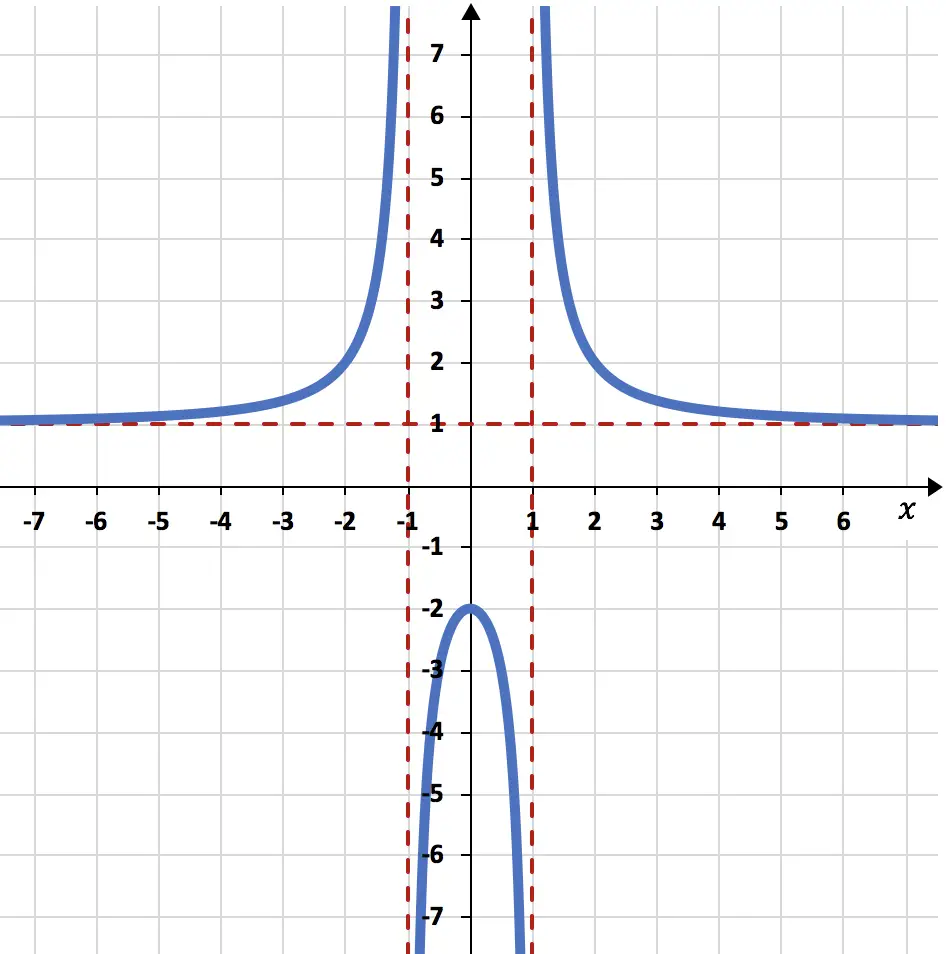
Gambarkan fungsi rasional berikut:
![]()
Untuk mencari domain suatu fungsi, kita atur penyebutnya sama. bawa pecahan ke nol dan selesaikan persamaan yang dihasilkan:
![]()
![]()
![]()
![]()
![]()
Kedua, kita menentukan ambang suatu fungsi dengan sumbu x sama dengan ekspresi aljabar fungsi tersebut. baja:
![]()
![]()
![]()
![]()
![]()
![]()
Tidak ada akar kuadrat dari bilangan negatif. Oleh karena itu, fungsinya tidak memotong sumbu X.
Dan untuk mencari titik potong dengan sumbu komputer, kita evaluasi fungsinya di x=0.
![]()
Maka titik potongnya dengan sumbu Y adalah:
![]()
Untuk melihat apakah suatu fungsi mempunyai asimtot vertikal, kita perlu menghitung limit fungsi tersebut di titik-titik yang tidak termasuk dalam domain tersebut (dalam hal ini x=-1 dan x=+1). Dan jika hasilnya tak terhingga, maka itu adalah asimtot vertikal. Belum:
![]()
Karena limit fungsi ketika x mendekati -1 menghasilkan tak terhingga, x=-1 adalah asimtot vertikal.
Kita menghitung batas lateral asimtot x=-1 dengan mensubstitusikan bilangan yang sangat dekat dengannya ke dalam fungsi:
![]()
![]()
Sekarang mari kita lihat apakah x=+1 merupakan asimtot vertikal:
![]()
Karena limit fungsi ketika x mendekati +1 menghasilkan tak terhingga, x=+1 adalah asimtot vertikal.
Kita menghitung batas lateral asimtot x=1 dengan mensubstitusi bilangan yang sangat dekat dengannya ke dalam fungsi:
![]()
![]()
Sebaliknya, asimtot horizontal suatu fungsi adalah hasil dari limit fungsi tersebut. Belum:
![]()
Limit tak terhingga dari fungsi tersebut menghasilkan 1, sehingga fungsi tersebut mempunyai asimtot horizontal di y=1.
Karena fungsi tersebut memiliki asimtot horizontal, maka fungsi tersebut tidak memiliki asimtot miring.
Kita bedakan fungsinya lalu pelajari interval kenaikan dan penurunannya:
![]()
![]()
Sekarang kita atur turunannya sama dengan 0 dan selesaikan persamaannya:
![]()
![]()
![]()
![]()
![]()
Kami mewakili pada garis semua titik kritis yang dihitung, yaitu titik yang tidak termasuk dalam domain (x=-1 dan x=+1) dan titik yang membatalkan turunan (x=0):

Dan kita evaluasi tanda turunannya pada setiap interval, untuk mengetahui apakah fungsinya naik atau turun. Oleh karena itu, kita mengambil sebuah titik di setiap interval (bukan titik tunggalnya) dan melihat tanda apa yang dimiliki turunannya pada titik tersebut:
![]()
![]()
![]()
![]()
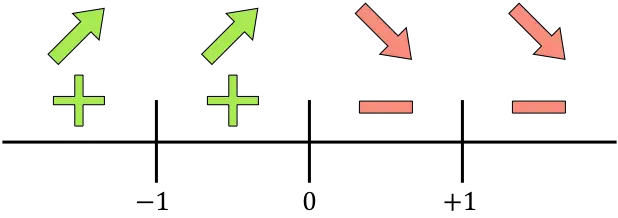
Fungsinya bertambah jika turunannya positif dan fungsinya berkurang jika fungsinya negatif:
Pertumbuhan:
![]()
Mengurangi:
![]()
Fungsinya berubah dari naik ke turun pada x=0, jadi x=0 adalah maksimum lokal dari fungsi tersebut.
Kami mengganti titik ekstrem yang ditemukan ke dalam fungsi asli untuk mencari koordinat Y dari titik tersebut:
![]()
Oleh karena itu, ekstrem relatif dari fungsi tersebut adalah:
Maksimal tepat sasaran
![]()
Untuk mempelajari kelengkungan suatu fungsi, kita menghitung turunan keduanya:
![f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}” title=”Rendered by QuickLaTeX.com”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-802852beb818dd5a0dce2f30374f3a88_l3.png) Semua istilah punya
Semua istilah punya
![]()
, maka kita dapat menyederhanakan pecahan tersebut:
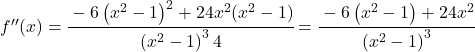
![]()
Sekarang kita atur turunan keduanya sama dengan 0 dan selesaikan persamaannya:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Tidak ada akar kuadrat dari bilangan negatif. Jadi tidak ada gunanya yang cocok
![]()
Sekarang kita nyatakan pada garis semua titik tunggal yang ditemukan, yaitu titik-titik yang tidak termasuk dalam domain (x=-1 dan x=+1) dan titik-titik yang menghilangkan turunan keduanya (dalam hal ini tidak ada setiap):
Dan kita evaluasi tanda turunan keduanya pada setiap interval, untuk mengetahui apakah fungsinya cekung atau cembung. Oleh karena itu, kita mengambil sebuah titik di setiap interval (tidak pernah berupa titik tunggal) dan melihat tanda apa yang dimiliki turunan kedua pada titik tersebut:
![]()
![]()
![]()

Jika turunan keduanya positif berarti fungsinya cembung.
![]()
, dan jika turunan keduanya negatif berarti fungsinya cekung
![]()
. Oleh karena itu, interval kecekungan dan kecembungan adalah:
Cembung
![]()
:
![]()
Cekung
![]()
:
![]()
Namun meskipun terjadi perubahan kelengkungan pada x=-1 dan x=1, hal tersebut bukanlah titik belok. Karena mereka tidak termasuk dalam domain fungsi.
Dan terakhir, kami membuat grafik fungsi tersebut menggunakan semua perhitungan yang dilakukan:
Latihan 3
Gambarkan fungsi rasional berikut pada grafik:
![]()
Ini adalah fungsi rasional, jadi kita perlu menetapkan penyebutnya sama dengan 0 untuk melihat bilangan mana yang tidak termasuk dalam domain fungsi tersebut:
![]()
![]()
![]()
![]()
![]()
Untuk mencari titik potong dengan sumbu X, kita selesaikan
![]()
Karena fungsi selalu bernilai 0 pada sumbu X:
![]()
![]()
![]()
![]()
![]()
Maka titik potongnya dengan sumbu X adalah:
![]()
Dan untuk mencari titik potong dengan sumbu Y, kita hitung
![]()
Karena x selalu 0 pada sumbu Y:
![]()
Maka titik potongnya dengan sumbu Y adalah:
![]()
Dalam hal ini, titik potong sumbu X bertepatan dengan titik potong sumbu Y, karena fungsi melewati titik asal.
Untuk melihat apakah suatu fungsi mempunyai asimtot vertikal, kita perlu menghitung limit fungsi tersebut di titik-titik yang tidak termasuk dalam domain (dalam hal ini x=-2 dan x=+2). Dan jika hasilnya tak terhingga, maka itu adalah asimtot vertikal. Belum:
![]()
Karena limit fungsi ketika x mendekati -2 menghasilkan tak terhingga, x=-2 adalah asimtot vertikal.
Kita menghitung batas lateral asimtot x=-2 dengan mensubstitusikan bilangan yang sangat dekat dengannya ke dalam fungsi:
![]()
![]()
Sekarang mari kita lihat apakah x=+2 merupakan asimtot vertikal:
![]()
Karena limit fungsi ketika x mendekati +2 menghasilkan tak terhingga, x=+2 adalah asimtot vertikal.
Kita menghitung batas lateral asimtot x=2 dengan mensubstitusi bilangan yang sangat dekat dengannya ke dalam fungsi:
![]()
![]()
Sebaliknya, asimtot horizontal suatu fungsi adalah hasil dari limit fungsi tersebut. Belum:
![]()
Limit tak terhingga dari fungsi tersebut menghasilkan +∞, sehingga fungsi tersebut tidak memiliki asimtot horizontal.
Kami sekarang menghitung asimtot miring. Asimtot miring berbentuk
![]()
DAN
![]()
Itu dihitung dengan rumus berikut:
![]()
![]()
![]()
Setelah kita mengetahui kemiringan asimtot miring, kita menentukan titik potongnya menggunakan rumus berikut:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-de4326a40acf34b64a28c9da8250bf00_l3.png)
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13478ac6f6fac958ec8b2a714c28bc3d_l3.png)
Tapi kita memperoleh ketidakpastian ∞ – ∞. Oleh karena itu, suku-suku tersebut perlu direduksi menjadi penyebut yang sama. Untuk melakukannya, kita mengalikan dan membagi x dengan penyebut pecahan:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e939b43a3405ba644d4b60bb4bacadb_l3.png)
![]()
![]()
Singkatnya, asimtot miringnya adalah:
![]()
![]()
![]()
Untuk mempelajari monotonisitas suatu fungsi, pertama-tama kita harus menghitung turunannya:
![]()
![]()
Sekarang kita atur turunannya sama dengan 0 dan selesaikan persamaannya:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc1f64cdcd293da4fee1ef02fff9a588_l3.png)
Sekarang kita nyatakan pada garis semua titik tunggal yang ditemukan, yaitu titik-titik yang tidak termasuk dalam domain (x=-2 dan x=+2) dan titik-titik yang membatalkan turunan (x=0, x=- 3,46 dan x= +3,46):

Dan kita evaluasi tanda turunannya pada setiap interval, untuk mengetahui apakah fungsinya naik atau turun. Oleh karena itu, kita mengambil sebuah titik di setiap interval (bukan titik tunggalnya) dan melihat tanda apa yang dimiliki turunannya pada titik tersebut:
![]()
![]()
![]()
![]()
![]()
![]()
Jika turunannya positif berarti fungsinya meningkat, dan jika turunannya negatif berarti fungsinya menurun. Oleh karena itu, interval pertumbuhan dan penurunannya adalah:
Pertumbuhan:
![]()
Mengurangi:
![]()
Fungsinya berubah dari naik ke turun pada x=-3,46, jadi x=-3,46 adalah maksimum dari fungsi tersebut. Dan fungsinya berubah dari menurun menjadi meningkat pada x=3,46, jadi x=3,46 adalah fungsi minimumnya.
Kami menentukan koordinat Y dari ujung relatif:
![]()
![]()
Oleh karena itu, ekstrem relatif dari fungsi tersebut adalah:
Maksimal tepat sasaran
![]()
Minimal untuk menunjuk
![]()
Untuk mempelajari kelengkungan suatu fungsi, kita menghitung turunan kedua dari fungsi tersebut:



![]()
![]()
![]()
![]()
Sekarang kita atur turunan keduanya sama dengan 0 dan selesaikan persamaannya:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]()
Tidak ada penyelesaian karena tidak ada akar negatif dari bilangan real.
Sekarang kita nyatakan pada garis semua titik tunggal yang ditemukan, yaitu titik-titik yang tidak termasuk dalam domain (x=-2 dan x=+2) dan titik-titik yang menghilangkan turunan kedua (x=0):

Dan kita evaluasi tanda turunan keduanya pada setiap interval, untuk mengetahui apakah fungsinya cekung atau cembung. Oleh karena itu, kita mengambil sebuah titik di setiap interval (tidak pernah berupa titik tunggal) dan melihat tanda apa yang dimiliki turunan kedua pada titik tersebut:
![]()
![]()
![]()
![]()

Jika turunan keduanya positif berarti fungsinya cembung.
![]()
, dan jika turunan keduanya negatif berarti fungsinya cekung
![]()
. Oleh karena itu, interval kecekungan dan kecembungan adalah:
Cembung
![]()
:
![]()
Cekung
![]()
:
![]()
Namun meskipun terjadi perubahan kelengkungan pada x=-2 dan x=+2, hal tersebut bukanlah titik belok. Karena x=-2 dan x=+2 tidak termasuk dalam domain fungsi tersebut. Sebaliknya pada x=0 terjadi perubahan kelengkungan (fungsi berubah dari cembung menjadi cekung) dan ini termasuk dalam fungsi tersebut, sehingga x=0 merupakan titik belok.
Kami mengganti titik belok yang ditemukan ke dalam fungsi asli untuk mencari koordinat titik belok lainnya:
![]()
Oleh karena itu, titik balik dari fungsi tersebut adalah:
Titik balik:
![]()
Terakhir, berdasarkan semua informasi yang telah kami hitung, kami merepresentasikan fungsinya:
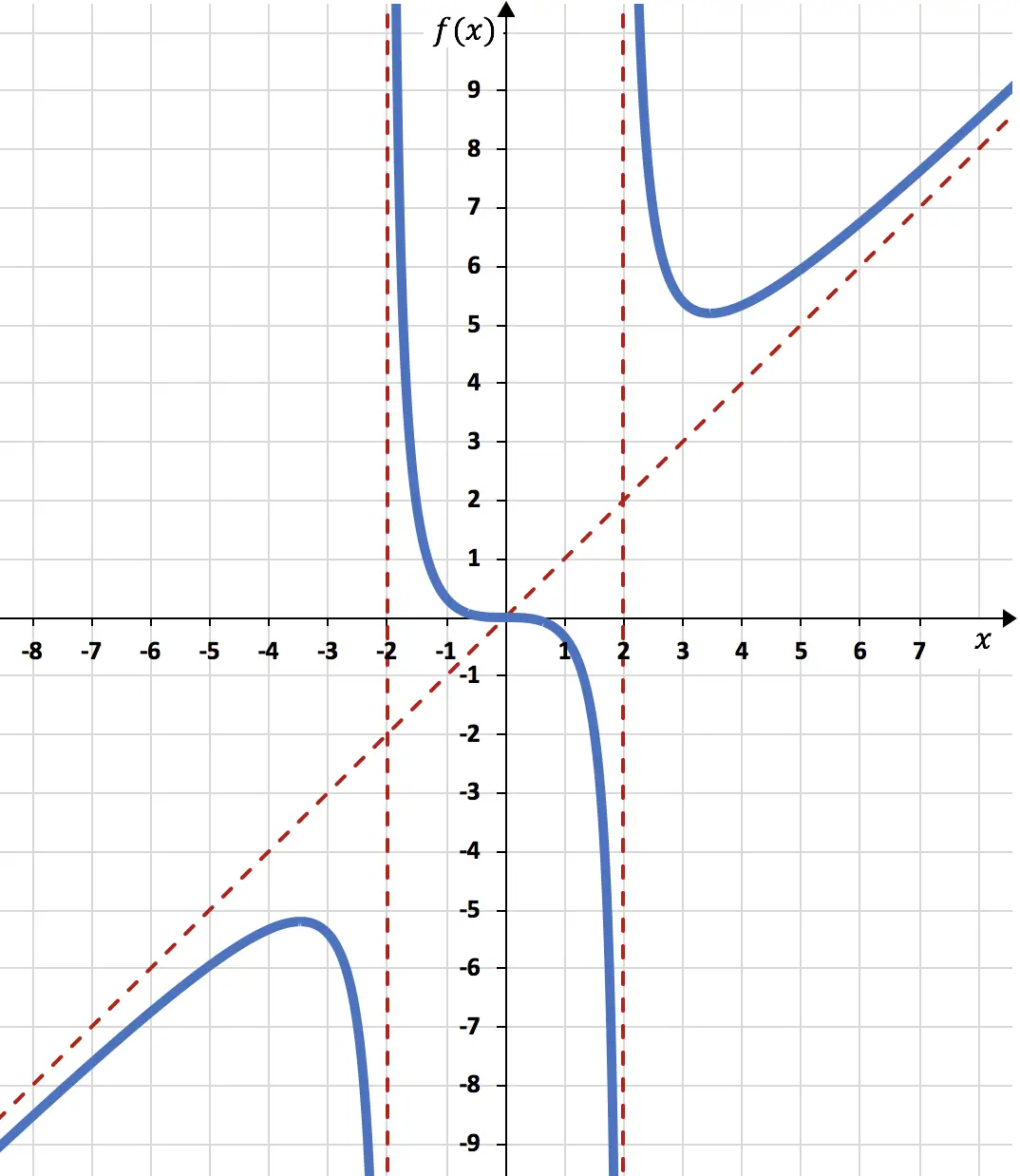
Komentar: Perhatikan bahwa fungsi tersebut memotong asimtot miring di suatu titik
![]()
Memang, asimtot miring terutama menentukan perilaku fungsi ketika x cenderung ke arah +∞ dan -∞, pada kenyataannya, fungsi tersebut tidak pernah melintasi asimtot miring di sebelah kanan grafik (x→+∞) dan di sebelah kiri grafik grafik (x→-∞). Namun, sangat jarang suatu fungsi melintasi asimtot miring di tengah, ini adalah kasus yang sangat istimewa.