Pada artikel ini kami akan menjelaskan cara mengetahui monotonisitas suatu fungsi, yaitu cara mencari interval kenaikan dan penurunan suatu fungsi. Selain itu, Anda dapat berlatih dengan latihan langkah demi langkah tentang pertumbuhan dan penurunan suatu fungsi.
Apa yang dimaksud dengan monotonisitas suatu fungsi?
Suatu fungsi bersifat monotonik pada suatu interval jika ia mempertahankan orde tertentu. Ada lima jenis monoton:
- Fungsi yang meningkat secara monoton: ketika nilai fungsi di suatu titik selalu sama dengan atau lebih besar dari nilai fungsi di titik sebelumnya.
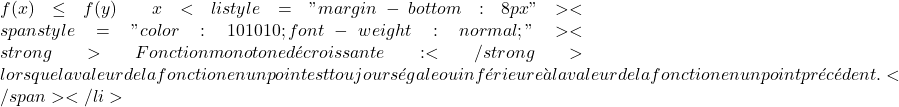 Fungsi yang meningkat secara monoton: ketika nilai fungsi di suatu titik selalu lebih besar dari nilai fungsi di titik sebelumnya.
Fungsi yang meningkat secara monoton: ketika nilai fungsi di suatu titik selalu lebih besar dari nilai fungsi di titik sebelumnya.
 Fungsi konstan bila nilai fungsi pada suatu titik selalu sama dengan nilai fungsi pada titik sebelumnya.
Fungsi konstan bila nilai fungsi pada suatu titik selalu sama dengan nilai fungsi pada titik sebelumnya.

![]()
x^2-4=0x^2=4x=\pm 2
![]()
\text{Dom } f= \mathbb{R}-\{+2, -2 \}
![]()
f(x)=\cfrac{3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-4) – 3\cdot 2x}{\left( x^2-4\kanan)^2}f'(x)=\cfrac{-6x}{\kiri(x^2-4\kanan)^2}
![]()
f'(x)=0\cfrac{-6x}{\kiri(x^2-4\kanan)^2}=0
![]()
\kiri(x^2-4\kanan)^2}
![]()
-6x=0\cdot \kiri(x^2-4\kanan)^2-6x=0x=\cfrac{0}{-6}x=0
![]()
f'(x)=0,



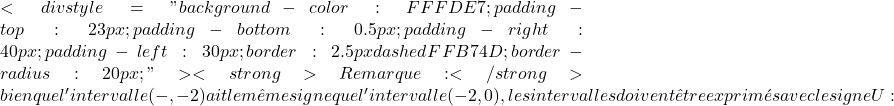
![]()
(-\infty,0)

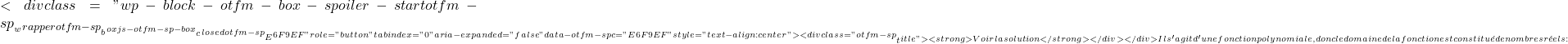
![]()
f'(x)=0.
![]()
f(x)=x^3-6x^2+9x \ \panah kanan panjang \ f'(x)=3x^2-12x+9
![]()
f'(x)= 03x^2-12x+9=0\begin{aligned}x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} = \cfrac{-(- 12) \pm \sqrt{(-12)^2-4\cdot 3 \cdot 9}}{2\cdot 3}=\\[2ex]&= \cfrac{+12 \pm \sqrt{144-108 }}{6} =\cfrac{12 \pm 6}{6}=\begin{kasus} \cfrac{12 + 6}{6}= 3 \\[4ex] \cfrac{12 – 6}{6} =1 \end{kasus} \end{sejajar}
![]()
f'(x)=0
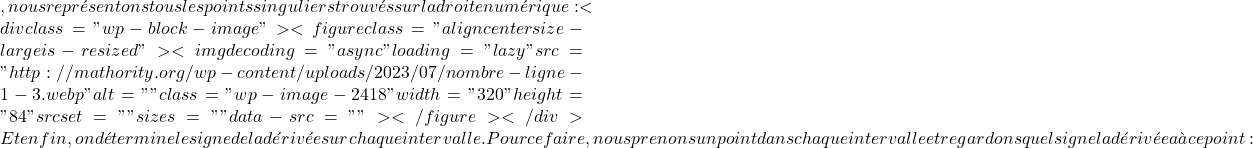


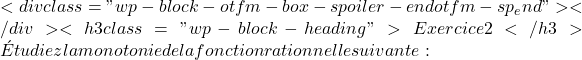
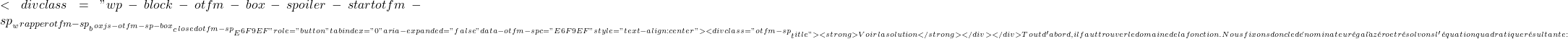
![]()
\text{Dom } f= \mathbb{R}-\{+3, -3 \}
![]()
f(x)=\cfrac{5}{x^2-9} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-9) – 5\cdot (2x)}{\ kiri(x^2-9\kanan)^2}f'(x)= \cfrac{-10x}{\kiri(x^2-9\kanan)^2}
![]()
f'(x)= 0\cfrac{-10x}{\kiri(x^2-9\kanan)^2}=0 -10x=0\cdot \kiri(x^2-9\kanan)^2 – 10x= 0 x= \cfrac{0}{-10} x=0
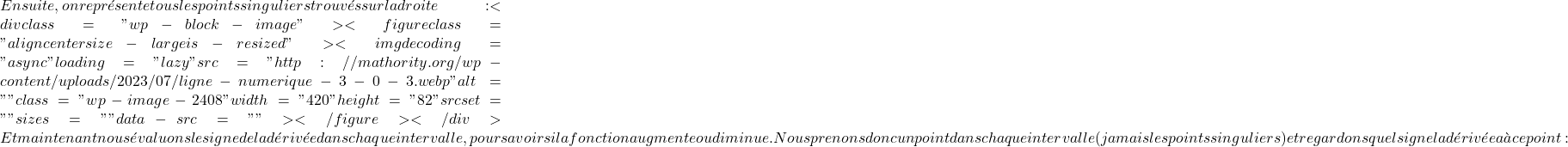


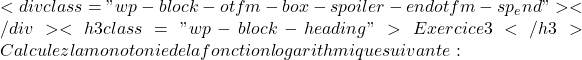
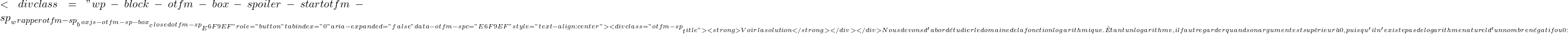
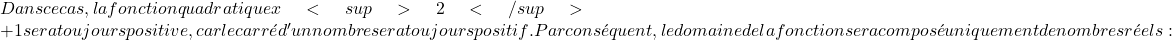
![]()
f(x)=\ln \bigl(x^2+1 \bigr) \ \longrightarrow \ f'(x)=\cfrac{1}{x^2+1 } \cdot (2x)f'(x) = \cfrac{2x}{x^2+1}
![]()
f'(x)= 0\cfrac{2x}{x^2+1}=0 2x=0\cdot \kiri(x^2+1\kanan) 2x= 0 x= \cfrac{0}{2} x=0


