Turunan dari arcsecant hiperbolik

Di sini Anda akan menemukan cara menghitung turunan dari garis potong busur hiperbolik suatu fungsi. Selain itu, Anda akan dapat melihat contoh penyelesaian turunan dari garis potong busur hiperbolik.

Rumus turunan busur hiperbolik

Turunan dari garis potong busur hiperbolik dari x sama dengan negatif 1 dibagi hasil kali x dengan akar satu dikurangi x kuadrat.

f(x)=\text{arcsech}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-1}{x\sqrt{1-x^2}}

Oleh karena itu, turunan garis potong busur hiperbolik suatu fungsi adalah dikurangi turunan fungsi tersebut dibagi dengan hasil kali fungsi tersebut dengan akar satu dikurangi fungsi kuadrat.

f(x)=\text{arcsech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1-u^2}}

Secara singkat rumus turunan fungsi arcsecant hiperbolik adalah:

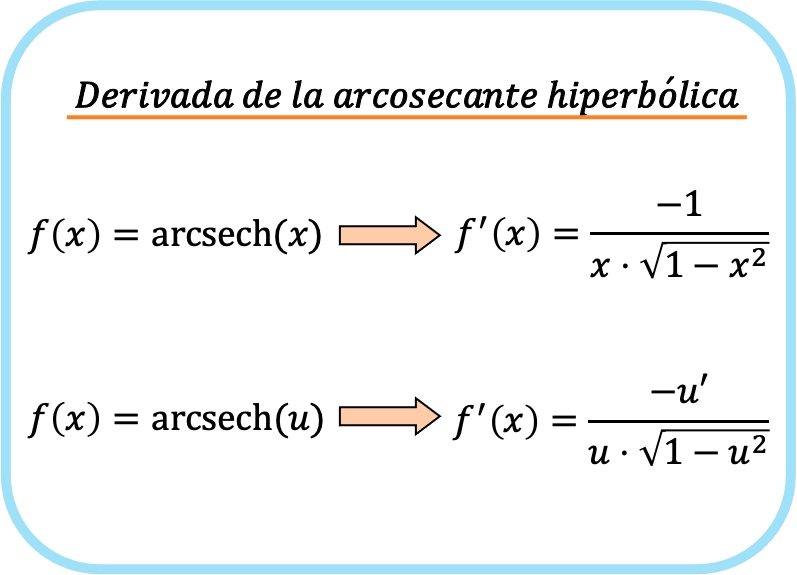
berasal dari arcsecant hiperbolik

Kedua ekspresi sebenarnya sesuai dengan rumus yang sama, namun aturan rantai diterapkan pada rumus kedua. Faktanya, jika Anda mensubstitusikan fungsi identitas x ke u, Anda akan mendapatkan rumus pertama karena turunan dari x adalah 1.

Contoh turunan dari arcsecant hiperbolik

Setelah melihat rumus turunan dari garis potong busur hiperbolik, kita akan menyelesaikan dua latihan langkah demi langkah jenis turunan trigonometri terbalik ini. Jadi, Anda dapat melihat dengan tepat cara menurunkan garis potong busur hiperbolik suatu fungsi.

Contoh 1

Pada contoh ini, kita akan menentukan turunan dari garis potong busur hiperbolik 2x.

f(x)=\text{arcsech}(2x)

Dalam argumen garis potong busur hiperbolik, kita mempunyai fungsi selain x, jadi kita perlu menggunakan rumus aturan rantai untuk menurunkannya:

f(x)=\text{arcsech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1-u^2}}

Fungsi 2x linier, jadi turunannya adalah 2. Oleh karena itu, untuk mencari turunannya, kita cukup mensubstitusikan 2x untuk u dan 2 untuk u’ ke dalam rumus:

f(x)=\text{arcsech}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-2}{2x\sqrt{1-(2x)^2}}=\cfrac{-2}{2x\sqrt{1-4x^2}}

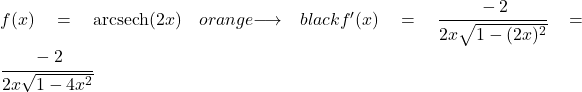
Contoh 2

Dalam latihan kedua ini, kita akan menurunkan garis potong busur hiperbolik dari fungsi polinomial:

f(x)=\text{arcsech}(x^3-4x)

Fungsi latihan ini bersifat majemuk, karena garis potong busur hiperbolik mempunyai fungsi lain dalam argumennya. Jadi kita perlu menggunakan rumus turunan busur hiperbolik dengan aturan rantai untuk melakukan penurunannya:

f(x)=\text{arcsech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1-u^2}}

Oleh karena itu, pada pembilang pecahan kita masukkan turunan dari fungsi polinomial argumen tersebut, dan pada penyebut kita ubah u dengan fungsi polinomial:

\begin{aligned}f(x)=\text{arcsech}(x^3-4x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(3x^2-4)}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\\[1.5ex] &=\cfrac{-3x^2+4}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\end{aligned}

Barang Serupa

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top