Pada artikel ini kami menjelaskan cara menurunkan kosekan hiperbolik suatu fungsi. Selain itu, Anda akan dapat melihat beberapa contoh penyelesaian turunan kosekan hiperbolik.
Rumus turunan dari kosekan hiperbolik
Turunan dari kosekan hiperbolik dari x sama dengan dikurangi kosekan hiperbolik dari x dikalikan kotangen hiperbolik dari x.
![]()
Oleh karena itu, turunan kosekan hiperbolik suatu fungsi adalah dikurangi hasil kali kosekan hiperbolik fungsi tersebut dikali kotangen hiperbolik fungsi tersebut dikalikan dengan turunan fungsi tersebut.
![]()
Singkatnya, rumus untuk menurunkan kosekan suatu fungsi adalah:
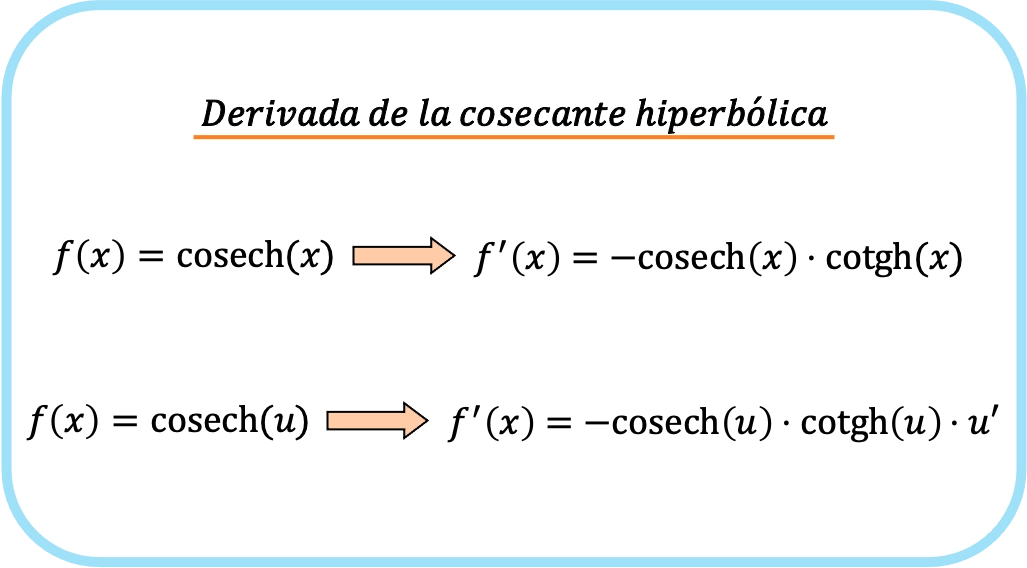
Faktanya, dua ekspresi sebelumnya sesuai dengan satu rumus, perbedaannya adalah aturan rantai diterapkan pada rumus kedua.
Contoh turunan dari kosekan hiperbolik
Setelah melihat apa rumus turunan kosekan hiperbolik, berikut beberapa contoh kerja turunan trigonometri jenis ini.
Contoh 1
Dalam contoh pertama ini, kita akan menurunkan kosekan hiperbolik dari x kuadrat:
![]()
Fungsi argumen kosekan hiperbolik berbeda dengan x, sehingga kita perlu menggunakan rumus turunan kosekan hiperbolik dengan aturan rantai.
![]()
Jadi, untuk menurunkan fungsi trigonometri ini, kita cukup mensubstitusikan nilai-nilai pada rumus sebelumnya, yaitu pada argumen kosekan hiperbolik dan tangen hiperbolik, kita masukkan x 2 , dan kalikan semuanya dengan turunannya dari x kuadrat, yaitu 2x:
![]()
Contoh 2
Dalam latihan ini, kita akan melihat berapa turunan dari kosekan hiperbolik dari x pangkat tiga:
![]()
Untuk mencari turunan kosekan hiperbolik suatu fungsi, kita menerapkan rumusnya:
![]()
Turunan dari x pangkat tiga adalah 3x 2 , jadi turunan seluruh fungsinya adalah:
![]()