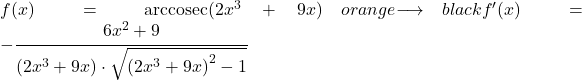Turunan dari busur kosekan

Di halaman ini Anda akan melihat rumus turunan arccosecant. Selain itu, Anda akan dapat melihat latihan yang diselesaikan untuk turunan dari kosekan busur suatu fungsi.

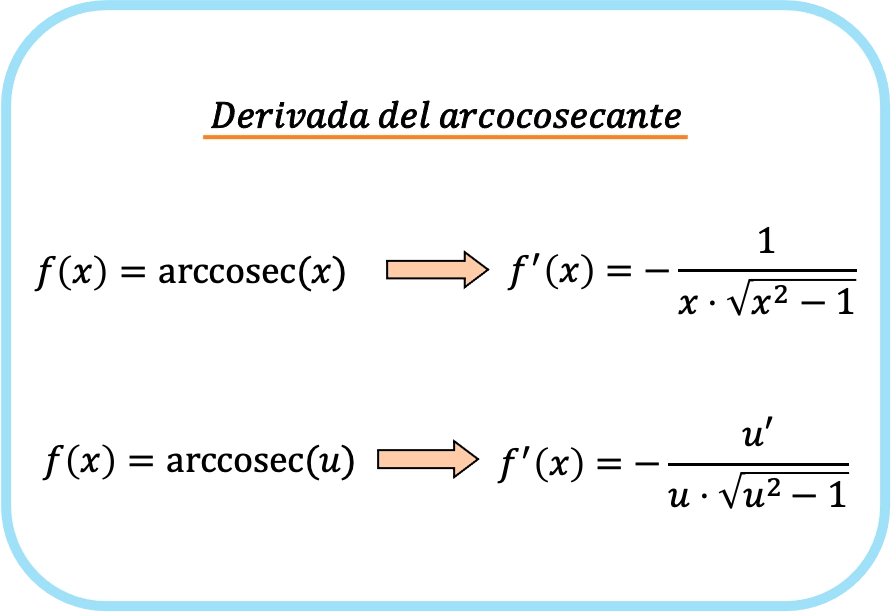
Rumus turunan arccosecant

Turunan arccosecant dari x adalah negatif satu perkalian x dengan akar x kuadrat dikurangi 1.

f(x)=\text{arccosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{x\cdot \sqrt{x^2-1}}

Oleh karena itu, turunan arccosecant suatu fungsi sama dengan dikurangi hasil bagi turunan fungsi tersebut dibagi fungsi dikalikan akar fungsi tersebut kuadrat dikurangi satu.

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

Faktanya, dua rumus sebelumnya sama, tetapi ekspresi kedua menerapkan aturan rantai. Faktanya, jika Anda mensubstitusi fungsi identitas x ke dalam u, Anda akan mendapatkan turunan arccosecant dari x karena turunan dari x adalah satu.

rumus turunan arccosecant

Seperti yang telah Anda ketahui, arccosecan merupakan kebalikan dari fungsi trigonometri dari cosecan, namun turunannya sangat berbeda. Rumus fungsi trigonometri jenis lainnya ini dapat Anda lihat pada link berikut:

➤ Lihat: turunan dari kosekan

Contoh turunan busur kosekan

Melihat apa itu aturan turunan arccosecant, selanjutnya kita akan menyelesaikan dua contoh turunan jenis ini. Namun jika Anda masih memiliki pertanyaan tentang cara menurunkan busur kosekan, Anda dapat menanyakannya kepada kami di komentar.

Contoh 1

Dalam contoh ini, kita akan melihat berapa turunan dari kosekan busur dari fungsi kuadrat x 2 .

f(x)=\text{arccosec}(x^2)

Untuk menghitung turunan arccosecant dari x kuadrat, kita menerapkan rumus yang kita lihat di atas:

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

Turunan x pangkat dua adalah 2x, jadi turunan fungsi gabungannya adalah:

f(x)=\text{arccosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{x^2\cdot \sqrt{\left(x^2\right)^2-1}}=-\cfrac{2x}{x^2\cdot \sqrt{x^4-1}}

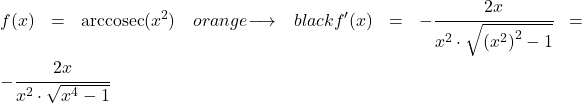
Contoh 2

Dalam contoh kedua ini, kita akan menurunkan arccosecant dari suatu fungsi potensial.

f(x)=\text{arccosec}(2x^3+9x)

Kita perlu menggunakan aturan turunan arcsecant untuk mencari turunan seluruh fungsi.

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

Jadi, di pembilangnya kita tuliskan turunan dari argumen fungsi tersebut, dan di penyebutnya kita tulis ulang fungsi potensialnya dan kalikan dengan akar kuadrat dari fungsi argumen tersebut, kuadrat dikurangi 1:

f(x)=\text{arccosec}(2x^3+9x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{6x^2+9}{(2x^3+9x)\cdot \sqrt{\left(2x^3+9x\right)^2-1}}

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top