Di sini Anda akan menemukan cara menurunkan tangen hiperbolik suatu fungsi. Anda juga akan dapat melihat contoh penyelesaian turunan trigonometri jenis ini dan, terakhir, kami akan menunjukkan rumus turunan tangen busur hiperbolik.
Rumus turunan dari tangen busur hiperbolik
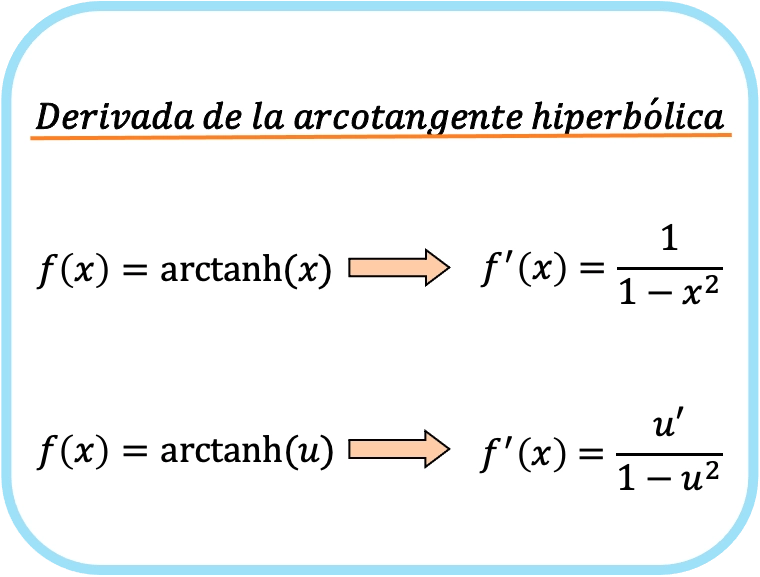
Turunan dari tangen busur hiperbolik x adalah satu per satu dikurangi x kuadrat.
![]()
Oleh karena itu, turunan tangen busur hiperbolik suatu fungsi sama dengan hasil bagi turunan fungsi tersebut dibagi satu dikurangi kuadrat fungsi tersebut.
![]()
Sebenarnya kedua rumus tersebut sama, namun pada rumus kedua diterapkan aturan rantai. Misalnya, mengganti x dengan u memberi kita rumus pertama karena turunan dari x adalah 1.
Sama seperti tangen busur yang merupakan kebalikan dari fungsi tangen, maka tangen busur hiperbolik adalah kebalikan dari tangen hiperbolik. Meski begitu turunannya sangat berbeda, turunan fungsi trigonometri ini bisa kamu cek di sini:
➤ Lihat: rumus turunan tangen hiperbolik
Contoh turunan dari arctangen hiperbolik
Contoh 1
![]()
Logikanya, kita harus menerapkan aturan turunan dari tangen busur hiperbolik:
![]()
Turunan dari 2x adalah 2, jadi masukkan dua pada pembilang pecahan dan satu dikurangi 2x kuadrat pada penyebutnya:
![]()
Contoh 2
![]()
Untuk menyelesaikan turunan fungsi ini, kita perlu menggunakan rumus turunan tangen busur hiperbolik.
![]()
Selain itu, fungsi argumen tangen busur hiperbolik adalah fungsi gabungan, jadi kita juga perlu menerapkan aturan rantai:
![]()
Bukti turunan dari tangen busur hiperbolik
Pada bagian akhir ini, kita akan mendemonstrasikan rumus turunan tangen busur hiperbolik.
![]()
Karena tangen busur hiperbolik adalah kebalikan dari tangen hiperbolik, kita dapat menyatakan persamaan sebelumnya dengan cara lain:
![]()
Sekarang kita bedakan kedua ruas persamaan:
![]()
Kami membersihkan Anda:
![]()
Sebaliknya, kita mengetahui bahwa selisih kuadrat kosinus hiperbolik dan sinus hiperbolik menghasilkan 1. Oleh karena itu, kita dapat mengubah ekspresi sebelumnya menjadi pecahan:
![]()
![]()
Kami membagi semua suku pecahan dengan kuadrat kosinus hiperbolik:
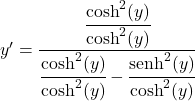
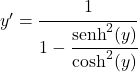
Hasil bagi sinus hiperbolik antara kosinus hiperbolik sama dengan tangen hiperbolik, oleh karena itu:
![]()
![]()
Namun, seperti yang kita lihat di awal pembuktian, garis singgung hiperbolik setara dengan variabel x, oleh karena itu kita dapat mensubstitusikan ekspresi tersebut sehingga memperoleh rumus turunan dari garis singgung busur hiperbolik:
![]()