Di sini Anda akan menemukan turunan dari arcsinus hiperbolik (rumus). Selain itu, Anda akan dapat melihat beberapa latihan yang diselesaikan pada turunan dari arcsinus hiperbolik suatu fungsi. Terakhir, kami tunjukkan rumus turunan fungsi trigonometri jenis ini.
Rumus turunan busur hiperbolik
Turunan busur hiperbolik x adalah satu pada akar kuadrat x kuadrat ditambah 1.
![]()
Jadi turunan busur hiperbolik suatu fungsi sama dengan hasil bagi turunan fungsi tersebut dibagi dengan akar kuadrat fungsi tersebut kuadrat ditambah satu.
![]()
Rumus kedua sama seperti rumus pertama namun menerapkan aturan rantai. Artinya, dengan rumus pertama, hanya busur hiperbolik dari xy yang dapat diturunkan, sedangkan dengan rumus kedua, busur hiperbolik dari fungsi apa pun dapat diturunkan.

Perlu diingat bahwa arcsinus hiperbolik merupakan kebalikan dari fungsi sinus hiperbolik, yang turunannya dapat Anda lihat di sini:
➤ Lihat: rumus turunan sinus hiperbolik
Contoh turunan busur hiperbolik
Contoh 1
![]()
Untuk menyelesaikan turunan fungsi arcsinus, kita menggunakan rumus seperti di atas:
![]()
Turunan dari 3x adalah 3, jadi pembilangnya adalah 3. Dan pada penyebutnya kita hanya perlu memasukkan akar kuadrat dari 3x kuadrat ditambah 1:
![]()
Contoh 2
![]()
Untuk menurunkan busur hiperbolik dari fungsi x pangkat tiga, kita harus menerapkan rumus yang sama:
![]()
Turunan dari x pangkat tiga adalah 3x 2 , jadi turunan dari sinus hiperbolik dari x yang dipangkatkan menjadi 3 adalah:
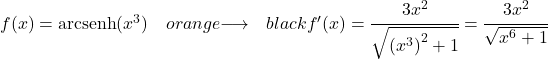
Bukti turunan arcsinus hiperbolik
Kami akan mendemonstrasikan rumus turunan dari busur hiperbolik:
![]()
Pertama, kita ubah arcsinus hiperbolik menjadi sinus hiperbolik:
![]()
Kami menyimpulkan dari kedua sisi persamaan:
![]()
Kami membersihkan Anda:
![]()
Kemudian kita terapkan identitas trigonometri yang menghubungkan sinus hiperbolik dan kosinus hiperbolik:
![]()
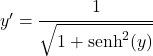
Namun di atas kita menyimpulkan bahwa x berhubungan dengan sinus hiperbolik dari y, sehingga persamaannya tetap:
![]()
Seperti yang Anda lihat, dengan menerapkan langkah-langkah ini kami memperoleh rumus turunan arcsinus hiperbolik, sehingga terbukti.