Berasal dari akar kata

Di sini kami menjelaskan cara mengambil turunan dari suatu akar (atau fungsi radikal). Anda akan menemukan rumus pembagian akar dan latihan yang diselesaikan langkah demi langkah untuk turunan akar.

Rumus turunan suatu akar

Turunan dari suatu akar, atau fungsi irasional, sama dengan turunan dari radikan (ekspresi di bawah akar) dibagi dengan hasil kali indeks dari akar dikalikan dengan akar yang sama, dengan mengurangkan 1 dari eksponen dari akar tersebut.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Namun, jika akar akarnya hanya x, rumusnya akan disederhanakan. Oleh karena itu, turunan akar dari x adalah sebagai berikut:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Singkatnya, ada dua rumus untuk mendapatkan akar: rumus pertama yang selalu dapat digunakan dan rumus kedua yang hanya dapat digunakan jika radikannya adalah x.

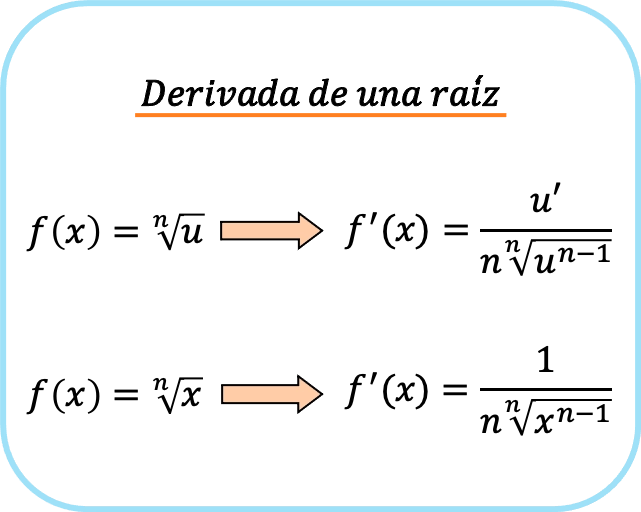
Jika dicermati, suku pada pembilang pecahan adalah suku yang dihasilkan dari penerapan aturan rantai saat mengambil turunan akar. Inilah sebabnya mengapa jika radikan adalah x, 1 muncul pada penyebutnya karena merupakan turunan dari x.

Contoh turunan akar

Mengingat rumus turunan fungsi radikal, berikut kami jelaskan beberapa contoh turunan jenis tersebut agar Anda memahami cara mengambil turunan suatu akar.

Contoh 1: Turunan dari akar kuadrat

Selanjutnya kita akan melihat turunan dari akar kuadrat:

$f(x)=\sqrt{x}$

Dalam hal ini, ekspresi di dalam akar hanyalah x, jadi kita bisa menggunakan rumus berikut:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Jadi turunan akar kuadrat sama dengan 1 dibagi hasil kali 2 kali akar kuadrat x:

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

Contoh 2: Turunan dari akar pangkat tiga

$f(x)=\sqrt[3]{x}$

Dalam contoh ini, ekspresi di bawah akar adalah x, jadi kita bisa menerapkan rumus berikut:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Jadi turunan akar pangkat tiga sama dengan 1 dibagi 3 kali akar pangkat tiga x kuadrat:

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

Contoh 3: Turunan dari akar keempat

$f(x)=\sqrt[4]{7x-2}$

Sekarang kita tidak memiliki x di bawah tanda radikal, tetapi kita memiliki ekspresi aljabar yang lebih kompleks. Oleh karena itu, kita harus menggunakan rumus umum turunan suatu akar:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Persamaan di bawah akar merupakan fungsi derajat satu, sehingga turunannya adalah 7. Jadi, turunan seluruh fungsi tersebut adalah:

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

Contoh 4: Penurunan dari satu akar ke akar lainnya

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

Untuk menyelesaikan turunan dari suatu akar yang tersusun dari akar lain, kita harus menerapkan rumus berikut:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Dalam hal ini, Anda harus menggunakan rumus yang sama dua kali berturut-turut untuk menghitung turunannya:

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

Memecahkan masalah turunan dari suatu akar

Hitunglah turunan dari akar-akar berikut:

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

lihat solusi

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

Rumus turunan suatu akar

Contoh turunan akar

Contoh 1: Turunan dari akar kuadrat

Contoh 2: Turunan dari akar pangkat tiga

Contoh 3: Turunan dari akar keempat

Contoh 4: Penurunan dari satu akar ke akar lainnya

Memecahkan masalah turunan dari suatu akar

Tinggalkan Komentar Batalkan Balasan