Di sini Anda akan menemukan asimtot vertikal suatu fungsi (dengan contoh). Kami juga menjelaskan cara mencari asimtot vertikal suatu fungsi dan, sebagai tambahan, Anda akan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah.
Apa yang dimaksud dengan asimtot vertikal?
Asimtot vertikal suatu fungsi adalah garis vertikal yang grafiknya mendekati tak terhingga tanpa pernah melintasinya. Oleh karena itu, persamaan asimtot vertikal adalah x=k , dengan k adalah nilai asimtot vertikal.
Artinya, k adalah asimtot vertikal jika limit fungsi ketika x mendekati k tidak terhingga.
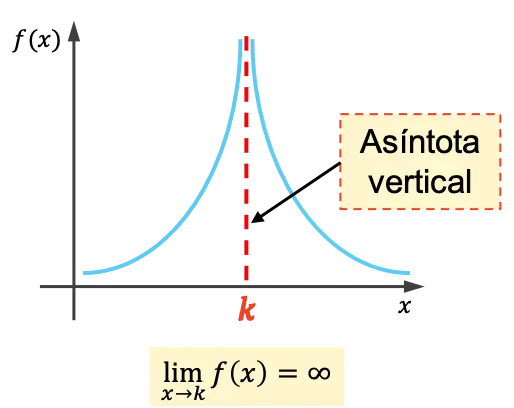
Cara menghitung asimtot vertikal suatu fungsi
Untuk menghitung asimtot vertikal suatu fungsi, langkah-langkah berikut harus diikuti:
- Temukan domain dari fungsi tersebut. Jika semua titik berada dalam domain, fungsi tersebut tidak memiliki asimtot vertikal.
- Hitung limit fungsi pada titik-titik yang tidak berada dalam domain.
- Asimtot vertikal dari fungsi tersebut adalah semua nilai yang limitnya memberikan tak terhingga.
Perhatikan bahwa suatu fungsi dapat memiliki lebih dari satu asimtot vertikal. Misalnya, grafik fungsi tangen memiliki banyak asimtot vertikal yang tak terhingga banyaknya.
➤ Lihat : ciri-ciri fungsi tangen
Contoh asimtot vertikal
Sebagai contoh, kita akan menemukan semua asimtot dari fungsi rasional berikut sehingga Anda dapat melihat cara kerjanya:
![]()
Secara umum, titik-titik yang terdapat asimtot vertikal tidak termasuk dalam domain fungsi. Oleh karena itu, pertama-tama kita akan menghitung domain dari fungsi tersebut.
Ini adalah fungsi rasional, jadi kita melihat saat penyebutnya hilang untuk menentukan titik-titik yang tidak termasuk dalam domain:
![]()
![]()
Oleh karena itu, domain dari fungsi tersebut adalah semua bilangan real kecuali x=2:
![]()
Jadi x=2 bisa menjadi asimtot vertikal dari fungsi tersebut. Untuk memverifikasi ini, kita harus menghitung limit fungsi pada titik ini:
![]()
Dalam hal ini kita telah memperoleh ketidakpastian suatu bilangan antara nol dan oleh karena itu, untuk menyelesaikan limitnya kita harus menghitung limit lateralnya untuk mengetahui apakah bilangan tersebut plus tak terhingga, dikurangi tak terhingga, atau limitnya tidak ada. Akan tetapi, ketika kita menghitung asimtot vertikal, kita tidak perlu melakukan batas lateral, namun memperoleh ketidakpastian ini sudah cukup untuk mengatakan bahwa ini adalah asimtot vertikal.
Singkatnya, karena limit fungsi ketika x mendekati 2 menghasilkan tak terhingga, x=2 adalah asimtot vertikal.
Di bawah ini adalah fungsi yang direpresentasikan secara grafis. Seperti yang Anda lihat, garis tersebut sangat dekat dengan garis x=2 (dari kiri dan kanan) namun tidak pernah berpotongan karena merupakan asimtot vertikal:

Selain itu, kita dapat menyimpulkan dari grafik batas lateral fungsi di titik x=2:
![]()
Memecahkan masalah asimtot vertikal
Latihan 1
Hitung asimtot vertikal dari fungsi rasional berikut:
![]()
Tidak ada rumus untuk menghitung asimtot vertikal suatu fungsi, tetapi Anda harus mencari domain fungsi tersebut dan melihat di titik mana fungsi tersebut tidak terdefinisi, limitnya memberikan tak terhingga.
Oleh karena itu, kita menetapkan penyebut fungsi rasional sama dengan 0 untuk mencari titik-titik yang tidak termasuk dalam domain:
![]()
![]()
![]()
Jadi, domain dari fungsi tersebut adalah semua bilangan real kecuali x=1/2:
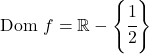
Jadi x=1/2 bisa menjadi asimtot vertikal. Untuk memeriksanya, kami menghitung limit fungsi pada titik ini:
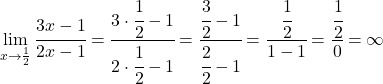
Jadi x=1/2 adalah asimtot vertikal , karena limit fungsi pada titik ini menghasilkan tak terhingga.
Latihan 2
Temukan semua asimtot vertikal dari fungsi pecahan berikut:
![]()
Pertama, kita atur penyebut pecahan menjadi nol untuk melihat nilai mana yang tidak berada dalam domain fungsi:
![]()
Kami memecahkan persamaan kuadrat tidak lengkap:
![]()
![]()
Oleh karena itu, domain dari fungsi rasional adalah:
![]()
Jadi, untuk menentukan mana dari dua nilai ini yang merupakan asimtot vertikal, kita mencari limit fungsi di setiap titik:
![]()
![]()
Kedua limit tersebut menghasilkan tak terhingga, jadi x=3 dan x=-3 adalah dua asimtot vertikal dari fungsi soal .
Latihan 3
Temukan, jika Anda punya, semua asimtot vertikal dari fungsi rasional berikut:
![]()
➤ Lihat: nol di antara nol ketidakpastian
Pertama, kita selesaikan persamaan penyebut kuadrat untuk mencari nilai yang menghilangkan penyebut pecahan:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9b2170358d5d1719077695aba5afa02e_l3.png)
Jadi domain fungsinya adalah:
![]()
Jadi, pertama-tama kita hitung limit fungsi tersebut di x=1:
![]()
Dan sebaliknya, kita menyelesaikan limit fungsi ketika x cenderung ke -3:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0e96a48986cd110e04058e3545290a0_l3.png)
Limit sebelumnya memberikan bentuk tak tentu nol di antara nol, jadi untuk menyelesaikannya kita perlu memfaktorkan polinomialnya. Jika Anda ragu tentang cara kami memecahkan batasan tersebut, Anda dapat melihat penjelasan lengkap tentang cara mengatasi ketidakpastian jenis ini di tautan ke pernyataan latihan.
Dalam hal ini, hanya limit fungsi di titik x=1 yang menghasilkan tak terhingga, jadi x=1 adalah satu-satunya asimtot vertikal fungsi tersebut .