Fungsi Identitas - Mathoritas

Di sini Anda akan menemukan apa itu fungsi identitas. Selain itu, Anda akan dapat melihat cara merepresentasikan fungsi identitas secara grafis dan apa saja karakteristiknya.

Apa yang dimaksud dengan fungsi identitas?

Fungsi identitas adalah fungsi yang gambarnya memiliki nilai yang sama dengan argumennya. Fungsi identitas dapat dinyatakan dengan istilah id .

Oleh karena itu, ekspresi matematika untuk fungsi identitas adalah:

$f(x)=x$

Misalnya bayangan fungsi identitas x=1 bernilai 1, bayangan x=2 bernilai 2, bayangan x=3 bernilai 3,…

$\begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}$

Fungsi identitas adalah contoh fungsi linier. Di tautan berikut Anda dapat melihat lebih banyak contoh fungsi jenis ini:

➤ Lihat: contoh fungsi linier

Representasi grafis dari fungsi identitas

Grafik fungsi identitas bersesuaian dengan garis yang merupakan garis bagi kuadran pertama dan ketiga.

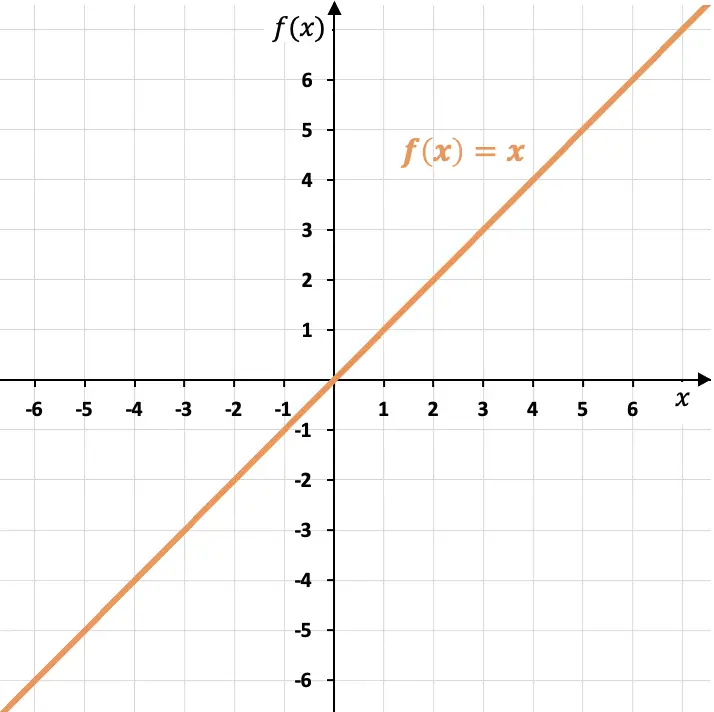
Seperti yang Anda lihat, fungsi identitas melewati titik asal (titik (0,0)) dan memiliki kemiringan sama dengan satu (m=1), karena satu satuan variabel bertambah dan untuk setiap nilai independen variabel X. Selain itu, fungsi identitas membentuk sudut 45º dengan sumbu X.

Ciri-ciri fungsi identitas

Fungsi identitas memiliki properti berikut:

Domain fungsi identitas adalah semua bilangan real:

$\text{Dom } f=\mathbb{R}$

Jangkauan (atau jangkauan) fungsi identitas juga terdiri dari semua bilangan real:

$\text{Im } f=\mathbb{R}$

Fungsi identitas merupakan fungsi kontinu dan bijektif.

Selain itu, fungsi identitas terdiri dari fungsi ganjil, artinya merupakan fungsi simetris terhadap titik asal koordinat.

$\displaystyle f(-x)=-f(x)$

➤ Lihat: fungsi simetris ganjil

Fungsi identitas meningkat di seluruh domainnya, dan kemiringannya sama dengan 1.

$m=1$

Memotong sumbu x (sumbu OX) dan sumbu y (sumbu Y) pada titik yang sama: titik asal koordinat.

$(0,0)$

Ini dapat diklasifikasikan sebagai fungsi polinomial derajat pertama.

Fungsi identitas bertindak sebagai elemen netral dari komposisi fungsi . Sehingga setiap fungsi yang dikomposisikan dengan fungsi identitas akan menghasilkan fungsi itu sendiri.

$f\circ id =id \circ f=f$

Nilai
$x=0$

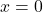
adalah satu-satunya akar dari jenis fungsi ini.

Limit fungsi identitas ketika x cenderung ke arah plus tak terhingga atau minus tak terhingga berturut-turut menghasilkan plus tak terhingga dan minus tak terhingga:

$\displaystyle\lim_{x\to +\infty} f(x)=+\infty$