Di sini Anda akan menemukan apa itu fungsi polinomial dan apa saja jenis fungsi polinomial. Selain itu, kami juga menjelaskan sifat-sifat fungsi polinomial.
Apa itu fungsi polinomial?
Fungsi polinomial adalah fungsi yang ekspresi aljabarnya berupa polinomial , yaitu fungsi polinomial yang ditentukan dengan penjumlahan atau pengurangan sejumlah suku berhingga yang derajatnya berbeda.
Oleh karena itu, fungsi polinomial dijelaskan secara matematis dengan ekspresi berikut:
![]()
Di sisi lain, fungsi polinomial juga dapat didefinisikan menggunakan rumus berikut:
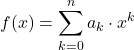
dimana syaratnya
![]()
Dan
![]()
masing-masing adalah koefisien dan variabel setiap monomial yang membentuk fungsi polinomial.
Syarat
![]()
, yang disebut suku utama, menunjukkan derajat fungsi polinomial, karena merupakan derajat monomial tertinggi dari fungsi tersebut. Dengan kata lain, nilai eksponen terbesar adalah nilai yang menunjukkan derajat fungsi polinomial.
Meskipun kita akan melihat lebih banyak karakteristik fungsi polinomial di bawah ini, domain dari setiap fungsi polinomial adalah bilangan real.
Jenis fungsi polinomial
Mengingat definisi fungsi polinomial, sekarang kita akan melihat semua jenis fungsi polinomial yang ada.
fungsi konstan
Fungsi konstanta merupakan fungsi polinomial berderajat 0, sehingga merupakan jenis fungsi yang selalu mengambil gambaran yang sama untuk setiap nilai variabel bebas (x).
Ekspresi umum fungsi konstanta adalah sebagai berikut:
![]()
Misalnya, tiga fungsi berikut merupakan konstanta atau fungsi polinomial berderajat nol:
![]()
Representasi grafis dari fungsi konstanta adalah garis horizontal (sejajar dengan sumbu x) yang nilainya sama dengan konstanta.

Anda dapat melihat lebih banyak fitur tentang jenis fungsi ini di tautan berikut:
➤ Lihat: ciri-ciri fungsi konstanta
Fungsi linear
Fungsi linier , disebut juga fungsi affine, adalah fungsi polinomial derajat pertama. Jadi fungsi polinomial jenis ini hanya dapat terdiri dari suku linier dan suku bebas:
![]()
Emas
![]()
adalah kemiringan garis dan
![]()
adalah perpotongan y, yaitu ketika fungsi tersebut memotong sumbu Y.
Contoh fungsi linier atau fungsi polinomial derajat satu:
![]()
Beberapa orang membedakan fungsi linier dari fungsi affine bergantung pada apakah fungsi tersebut memiliki sukunya
![]()
atau tidak, menjadi fungsi affine dengan intersep dan fungsi linier tanpa intersep.
Representasi grafis dari fungsi linier selalu berupa garis yang derajat kemiringannya bergantung pada nilai kemiringan fungsi tersebut.
Di bawah ini Anda dapat melihat secara grafis fungsi polinomial derajat pertama
![]()

Namun, untuk membuat grafik fungsi linier, Anda harus memahami beberapa konsep dengan jelas. Di tautan berikut Anda akan menemukan penjelasan langkah demi langkah tentang cara membuat grafik fungsi polinomial jenis ini:
➤ Lihat: Representasi grafis dari fungsi linier
Fungsi kuadrat
Fungsi kuadrat adalah fungsi polinomial berderajat 2, yaitu fungsi yang suku derajat tertingginya berderajat dua.
Oleh karena itu, rumus fungsi kuadrat adalah:
![]()
Emas
![]()
adalah suku kuadrat,
![]()
suku linier dan
![]()
suku bebas dari fungsi polinomial.
Contoh fungsi kuadrat atau fungsi polinomial kuadrat:
![]()
Grafik fungsi kuadrat selalu berbentuk parabola dan bentuknya bergantung pada tanda koefisien terdepan.
![]()
- Jika koefisien

positif, fungsi kuadratnya cembung (berbentuk seperti

).
- Sebaliknya, jika koefisiennya

negatif, fungsi kuadratnya cekung (berbentuk seperti

).


Jadi, dengan tanda koefisien utama fungsi polinomial kuadrat, kita dapat mengetahui bentuk grafiknya, namun untuk membuat representasi grafis yang tepat harus mengikuti prosedur tertentu. Anda dapat melihat prosedur ini di tautan berikut:
➤ Lihat: Representasi grafis dari fungsi kuadrat
fungsi kubik
Fungsi kubik adalah fungsi polinomial derajat ketiga. Oleh karena itu, fungsi polinomial jenis ini dinyatakan secara aljabar sebagai berikut:
![]()
Contoh fungsi kubik atau fungsi polinomial derajat ketiga:
![]()
![]()
Representasi grafis dari fungsi kubik sesuai dengan kurva kubik. Namun, untuk merepresentasikan fungsi jenis ini dalam grafik, prosedur yang rumit harus diikuti (termasuk turunannya). Anda dapat melihat cara melakukannya di sini:
➤ Lihat: Cara merepresentasikan suatu fungsi
Seperti yang Anda lihat, jenis fungsi polinomial sebenarnya tidak terbatas, karena polinomial dapat memiliki suku-suku yang tidak terbatas. Jadi, misalnya fungsi kuartik sama dengan fungsi kubik tetapi dengan penambahan suku kuadrat. Yang penting Anda memahami bahwa jenis fungsi polinomial ditandai dengan derajat fungsinya.
Sifat-sifat fungsi polinomial
Fungsi polinomial mempunyai ciri-ciri sebagai berikut:
- Domain dari setiap fungsi polinomial adalah himpunan bilangan real.
![]()
- Semua fungsi polinomial kontinu.
- Fungsi polinomial yang derajatnya lebih besar dari 1 tidak mempunyai asimtot.
- Terlepas dari jenis fungsi polinomialnya, satu-satunya titik potong dengan sumbu ordinat (sumbu Y) adalah pada tinggi suku bebasnya, yaitu pada titik berikut:
![]()
- Sebaliknya, suatu fungsi polinomial memotong sumbu absis (sumbu X), paling banyak, sebanyak derajat fungsi tersebut.
- Jika suatu fungsi polinomial hanya mempunyai suku-suku yang berderajat genap, berarti fungsi tersebut simetris terhadap sumbu OY. Sebaliknya, jika suatu fungsi polinomial hanya mempunyai suku-suku berderajat ganjil, berarti fungsi tersebut simetris terhadap titik asal koordinat.
- Banyaknya ekstrem relatif (maksimum atau minimum) suatu fungsi polinomial, paling banyak, adalah derajat polinomial fungsi tersebut dikurangi 1.
- Banyaknya titik belok suatu fungsi polinomial paling banyak sama dengan derajat polinomial fungsi tersebut dikurangi 2.
- Operasi dapat dilakukan dengan fungsi polinomial:
- Jumlah dua fungsi polinomial menghasilkan fungsi polinomial lainnya.
- Hasil kali dua fungsi polinomial menimbulkan fungsi polinomial lainnya.
- Mengalikan fungsi polinomial dengan skalar (bilangan real) menghasilkan fungsi polinomial yang serupa tetapi grafiknya diperkecil atau diperluas.
- Komposisi dua fungsi polinomial sama dengan fungsi polinomial lainnya.