Pada artikel ini kami akan menjelaskan apa itu fungsi simetris (fungsi genap dan ganjil) dan cara mempelajari simetri suatu fungsi. Anda juga akan dapat melihat properti dari jenis fungsi ini dan, terakhir, Anda akan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah fungsi simetris.
Apa yang dimaksud dengan fungsi simetris?
Fungsi simetris adalah fungsi yang sumbu simetrinya dapat ditemukan dalam representasi grafisnya. Ada dua jenis fungsi simetris: fungsi genap, simetris terhadap sumbu Y, dan fungsi ganjil, simetris terhadap titik asal.
Ingatlah bahwa sumbu simetri adalah garis khayal yang membagi suatu benda menjadi dua bagian sehingga titik-titik yang berlawanan berjarak sama satu sama lain.
bahkan fungsi
Fungsi genap adalah fungsi yang simetris terhadap sumbu y, artinya sumbu Y merupakan sumbu simetri fungsi tersebut.
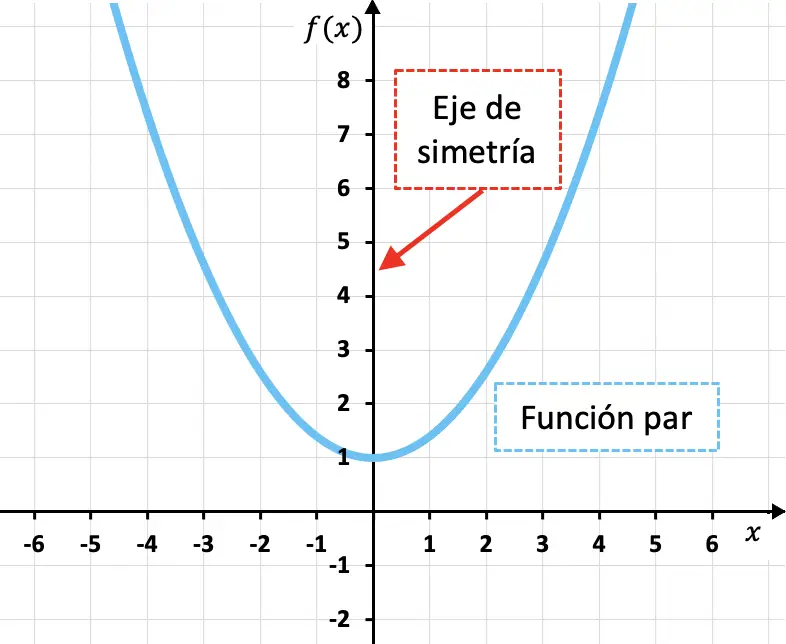
Seperti yang Anda lihat pada fungsi kuadrat di atas, gambaran fungsi genap untuk sembarang nilai variabel bebas (x) ekuivalen dengan gambaran fungsi untuk nilai kebalikannya (-x). Dengan kata lain, secara matematis, suatu fungsi genap jika memenuhi syarat berikut:
![]()
Fungsi genap merupakan salah satu jenis fungsi simetris, sekarang mari kita lihat seperti apa fungsi ganjil.
fungsi aneh
Fungsi ganjil adalah fungsi yang simetris terhadap titik asal, yaitu terhadap titik (0,0).
Di bawah ini Anda dapat melihat grafik fungsi ganjil:
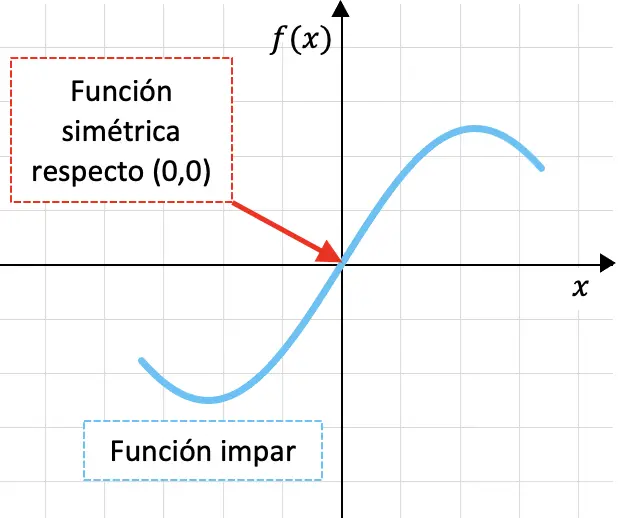
Fakta bahwa suatu fungsi simetris terhadap titik asal koordinat berarti jika kita melipat grafik fungsi terlebih dahulu melalui sumbu OY dan kemudian melalui sumbu OX, grafik fungsi tersebut akan tumpang tindih.
Secara aljabar, suatu fungsi ganjil jika hubungan antara gambar-gambarnya terpenuhi:
![]()
Mengetahui simetri suatu fungsi sangat berguna untuk merepresentasikannya, karena dengan mengetahui hanya separuh grafik kita dapat dengan cepat menggambar bagian lainnya.
Cara mencari simetri suatu fungsi
Untuk mempelajari simetri suatu fungsi, kita harus menghitung bayangannya
![]()
, artinya perlu untuk menghitung
![]()
Jadi, bergantung pada hasil bayangannya, simetri fungsinya adalah:
- jika sudah terisi
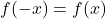
, fungsinya genap dan oleh karena itu simetris terhadap sumbu Y.
- jika sudah terisi
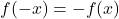
, fungsinya ganjil sehingga simetris terhadap titik asal.
- Jika tidak ada satupun syarat di atas yang terpenuhi maka fungsi tersebut merupakan fungsi asimetris (tidak mempunyai sumbu simetri).
Sebagai contoh, mari kita analisis simetri fungsi kubik berikut:
![]()
Untuk mempelajari simetri fungsi, kita menghitung
![]()
![]()
Ekspresi aljabar yang dihasilkan setara dengan ekspresi fungsi aslinya tetapi telah berubah tanda, atau dengan kata lain persamaan berikut terpenuhi:
![]()
Oleh karena itu, fungsinya ganjil dan karenanya simetris terhadap titik asal koordinat (0,0).
Sifat-sifat fungsi simetris
Fungsi simetris mempunyai ciri-ciri sebagai berikut:
- Jumlah dua fungsi genap/ganjil sama dengan fungsi genap/ganjil lainnya.
- Hasil kali dua fungsi genap atau dua fungsi ganjil menghasilkan fungsi genap.
- Turunan fungsi genap/ganjil adalah fungsi genap/ganjil.
- Komposisi antara dua fungsi genap/ganjil setara dengan fungsi genap/ganjil.
- Satu-satunya fungsi yang genap dan ganjil, yaitu simetris terhadap sumbu OY dan terhadap titik asal, adalah fungsi
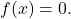
Menyelesaikan masalah simetri suatu fungsi
Latihan 1
Temukan simetri fungsi berikut:
![]()
Untuk menghitung simetri suatu fungsi, kita perlu mengevaluasi
![]()
![]()
Pangkat apa pun dari bilangan negatif yang dipangkatkan menjadi eksponen akan menghasilkan bilangan positif, sehingga persamaan berikut ini benar:
![]()
Oleh karena itu, fungsinya genap dan, oleh karena itu, simetris terhadap sumbu y (sumbu Y).
Latihan 2
Pelajari simetri fungsi rasional berikut:
![]()
Untuk menentukan simetri fungsi, kita lakukan
![]()
![]()
Dalam soal ini, kondisi simetri tidak terpenuhi, karena bayangannya
![]()
tidak sama dengan
![]()
juga tidak ke
![]()
![]()
Oleh karena itu, fungsi tersebut tidak memiliki sumbu simetri, melainkan fungsi asimetris.
Latihan 3
Hitung simetri fungsi berikut:
![]()
Untuk menganalisis simetri suatu fungsi, kita perlu menghitung
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d939238f353c0ab70492a66466dd0569_l3.png)
Dalam hal ini ekspresi yang dihasilkan sama seperti ekspresi aslinya tetapi dengan perubahan tanda, sehingga persamaan berikut terpenuhi:
![]()
Oleh karena itu, fungsinya ganjil dan karenanya simetris terhadap titik asal koordinat (0,0).