Pada artikel ini kami menjelaskan apa itu fungsi konstanta dan apa representasi grafisnya. Selain itu, Anda juga akan melihat beberapa contoh fungsi konstanta dan semua ciri-ciri dari jenis fungsi tersebut. Dan, akhirnya, Anda akan dapat berlatih dengan latihan fungsi konstan yang terselesaikan.
Apa yang dimaksud dengan fungsi konstanta?
Fungsi konstanta adalah fungsi yang selalu mempunyai gambaran yang sama untuk setiap nilai variabel bebas (x) , yaitu fungsi konstanta berbentuk f(x)=k , dimana k adalah bilangan real apa pun.
![]()
Representasi grafis dari fungsi konstanta adalah garis horizontal.
Misalnya, semua fungsi berikut adalah konstanta:
![]()
Representasi grafis dari fungsi konstan
Setelah kita melihat konsep fungsi konstanta, kita akan melihat cara merepresentasikan fungsi konstanta dalam grafik.
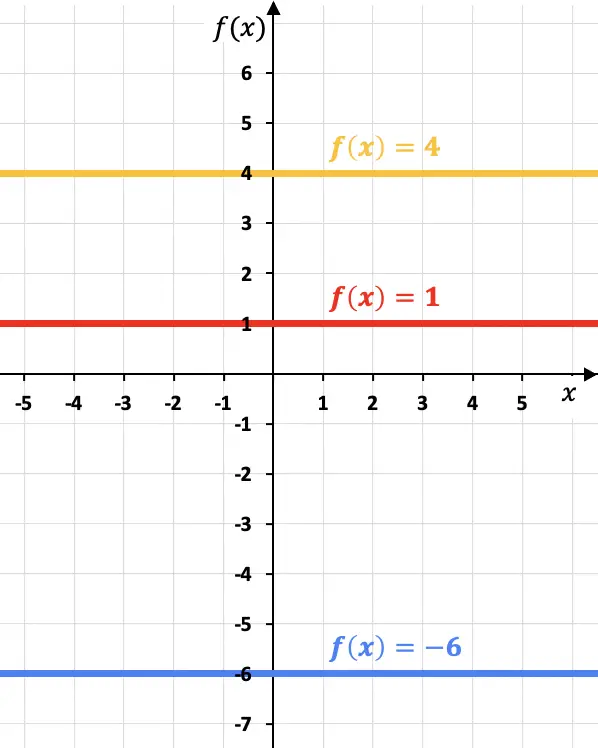
Membuat grafik fungsi konstanta cukup sederhana, cukup menggambar garis horizontal pada nilai fungsi (k).
Lihatlah contoh berikut di mana kita telah merepresentasikan tiga fungsi konstanta yang berbeda pada sebuah grafik:

Perhatikan bahwa setiap fungsi konstanta sejajar dengan sumbu x.
Di sisi lain, perlu diingat bahwa garis vertikal bukanlah fungsi konstan. Faktanya, garis vertikal bahkan bukan sebuah fungsi, karena menurut definisi suatu fungsi hanya dapat memiliki satu gambar untuk setiap nilai x.
Karakteristik fungsi konstanta
Selanjutnya kita akan menganalisis sifat-sifat fungsi konstanta. Pertimbangkan fungsi konstan dengan nilai berapa pun:
![]()
- Domain dari fungsi konstanta adalah semua bilangan real:
![]()
- Jalur atau rentang fungsi konstanta hanyalah nilai konstanta:
![]()
- Ini adalah fungsi kontinu dan genap, karena fungsinya selalu bernilai sama:
![]()
- Fungsi konstanta tidak bertambah atau berkurang, merupakan jenis fungsi yang selalu mempunyai kemiringan nol:
![]()
- Itu selalu memotong sumbu OY di titik (0,k).
![]()
- Setiap fungsi konstanta adalah polinomial yang berderajat nol.
- Ya
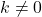
fungsi konstanta tidak memiliki akar, sebaliknya jika
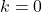
semua bilangan real adalah akar dari fungsi konstanta.
- Limit fungsi konstanta ketika x mendekati plus tak terhingga atau dikurangi tak terhingga sama dengan nilai konstanta:
![]()
![]()
- Turunan dari fungsi konstanta selalu nol:
![]()
Faktanya, definisi fungsi konstan juga dapat dilakukan dari pengertian turunan: suatu fungsi adalah konstan jika turunannya hilang di seluruh domainnya.
- Integral fungsi konstanta adalah fungsi linier (atau affine):
![]()
➤ Lihat: Apa itu fungsi linier?
Fungsi konstan pada suatu interval
Kita telah melihat bagaimana suatu fungsi bersifat konstan, namun suatu fungsi hanya dapat konstan dalam suatu interval domainnya.
Untuk memahami konsep ini, Anda perlu mengetahui fungsi mana saja yang didefinisikan secara potongan-potongan, jadi sebelum melanjutkan sebaiknya simak penjelasan berikut ini:
➤ Lihat: Apa yang dimaksud dengan fungsi sepotong-sepotong?
Setelah Anda mengetahui jenis-jenis fungsi ini, lihatlah fungsi yang didefinisikan pada bagian di bawah ini:

Seperti yang Anda lihat dari grafik, fungsinya tidak konstan di semua bilangan dalam domainnya. Namun konstan pada interval [-2,4), sehingga merupakan fungsi konstan hanya pada satu interval.
Masalah Memperbaiki Fungsi Konstan
Latihan 1
Tentukan manakah fungsi berikut yang merupakan konstanta:
![]()
Fungsi pertama,
![]()
, adalah fungsi konstan karena selalu 4 berapa pun nilai yang diambil variabel x.
Fungsi kedua,
![]()
, bukan merupakan fungsi konstan karena nilai fungsinya berubah-ubah bergantung pada nilai x. Ini adalah fungsi affine.
Fungsi ketiga,
![]()
, selalu sama dengan 0 untuk setiap nilai x, sehingga memang merupakan fungsi konstan.
Fungsi keempat,
![]()
, bukan fungsi konstan karena bervariasi bergantung pada nilai x. Ini adalah fungsi linier.
Latihan 2
Temukan fungsi konstanta yang melalui titik (0,6).
Secara aljabar, rumus fungsi konstanta selalu mempunyai bentuk yang sama:
![]()
Dan secara grafis fungsi konstanta selalu berupa garis mendatar, oleh karena itu koordinat fungsi konstanta selalu sama dan bernilai
![]()
Karena titik yang dilalui fungsi tersebut memiliki koordinat y=6, konstanta fungsi yang kita cari dalam soal ini pasti:
![]()
Latihan 3
Plot fungsi konstanta berikut pada grafik yang sama:
![]()
Untuk merepresentasikan setiap fungsi konstanta, cukup gambarkan garis horizontal lurus pada ketinggian setiap konstanta: