Fungsi tangen hiperbolik

Di halaman ini Anda akan menemukan segala sesuatu tentang garis singgung hiperbolik: apa rumusnya, representasi grafisnya, semua karakteristiknya,…

Rumus tangen hiperbolik

Fungsi tangen hiperbolik merupakan salah satu fungsi hiperbolik utama dan dilambangkan dengan simbol tanh(x) . Secara matematis, tangen hiperbolik sama dengan sinus hiperbolik dibagi kosinus hiperbolik.

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Dari rumus sinus hiperbolik dan rumus kosinus hiperbolik, kita dapat memperoleh persamaan berikut:

$\text{tanh}(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}$

Oleh karena itu, fungsi tangen hiperbolik berhubungan dengan fungsi eksponensial. Di tautan berikut Anda dapat melihat semua karakteristik dari jenis fungsi ini:

➤ Lihat: ciri-ciri fungsi eksponensial

Representasi grafis dari garis singgung hiperbolik

Dari rumusnya, secara grafis kita dapat merepresentasikan fungsi tangen hiperbolik:

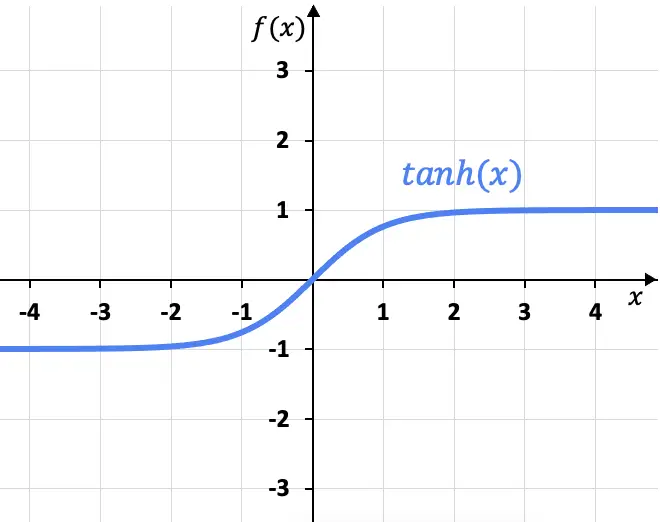
Seperti dapat dilihat dari grafik, fungsi tangen hiperbolik memiliki dua asimtot horizontal di x=+1 dan x=-1, karena limit fungsi ketika x mendekati plus tak terhingga menghasilkan x=+1, dan limit hingga minus tak terhingga memberikan x=-1.

Sebaliknya, grafik garis singgung hiperbolik tidak ada hubungannya dengan grafik garis singgung (fungsi trigonometri) yang merupakan fungsi periodik. Gambaran grafis garis singgung dan perbedaannya dengan garis singgung hiperbolik dapat Anda lihat pada tautan berikut:

➤ Lihat: representasi grafis dari fungsi tangen

Ciri-ciri garis singgung hiperbolik

Fungsi tangen hiperbolik mempunyai sifat sebagai berikut:

Domain fungsi tangen hiperbolik adalah semua bilangan real.

$\text{Dom } f = \mathbb{R}$

Sebaliknya, jalur atau rentang fungsi tangen hiperbolik dibatasi pada nilai antara -1 dan +1 (tidak inklusif).

$\text{Im } f= (-1,1)$

Garis singgung hiperbolik merupakan fungsi kontinu, bijektif, dan ganjil (simetris terhadap titik asal).

$\displaystyle \text{tanh}(-x) =- \text{tanh}(x)$

Fungsi tersebut memotong sumbu X dan sumbu Y di titik asal koordinat.

$(0,0)$

Batasan plus/minus tak terhingga dari fungsi tangen hiperbolik menghasilkan +1/-1. Oleh karena itu, fungsi tersebut memiliki asimtot horizontal di x=+1 dan asimtot horizontal lainnya di x=-1.

$\displaystyle\lim_{x\to+\infty}\text{tanh}(x)=+1$

$\displaystyle\lim_{x\to-\infty}\text{tanh}(x)=-1$

Garis singgung hiperbolik meningkat tajam di seluruh domainnya, oleh karena itu ia tidak memiliki ekstrem relatif (tidak maksimum maupun minimum).

Namun fungsi tersebut berubah dari cembung menjadi cekung di titik x = 0, sehingga x = 0 merupakan titik belok fungsi tersebut.

Kebalikan dari fungsi tangen hiperbolik disebut argumen tangen hiperbolik (atau tangen hiperbolik) dan rumusnya adalah sebagai berikut:

$\displaystyle\text{tanh}^{-1}(x)=\text{arg tanh}(x)=\cfrac{1}{2}\ln\left(\frac{1+x}{1-x}\right)$

Turunan fungsi tangen hiperbolik adalah 1 dibagi kuadrat kosinus hiperbolik:

$f(x)=\text{tanh}(x) \ \longrightarrow \ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=1-\text{tanh}^2(x)$

Integral fungsi tangen hiperbolik adalah logaritma natural dari kosinus hiperbolik:

$\displaystyle\int\text{tanh}(x) \ dx= \ln\Bigl(\text{cosh}(x)\Bigr)+C$

Garis singgung hiperbolik dari penjumlahan dua bilangan berbeda dapat dihitung dengan menerapkan persamaan berikut:

$\text{tanh}(x+y)=\cfrac{\text{tanh}(x)+\text{tanh}(y)}{1+\text{tanh}(x)\cdot \text{tanh}(y)}$

Polinomial Taylor atau deret tangen hiperbolik memiliki jari-jari konvergensi
$\left|x\right|<\cfrac{\pi}{2}$

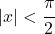
dan sesuai dengan ekspresi berikut:

$\displaystyle\text{tanh}(x)=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots =\sum_{n=1}^\infty\frac{2^{2n}(2^{2n}-1)B_{2n} x^{2n-1}}{(2n)!}$

Emas

$B_n$

adalah bilangan Bernoulli .

Rumus tangen hiperbolik

Representasi grafis dari garis singgung hiperbolik

Ciri-ciri garis singgung hiperbolik

Tinggalkan Komentar Batalkan Balasan