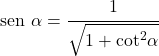Di halaman ini Anda akan menemukan segala sesuatu tentang fungsi sinus: apa itu fungsi sinus, apa rumusnya, cara merepresentasikannya dalam grafik, ciri-ciri fungsi jenis ini, amplitudo, periode, dll. Selain itu, Anda akan dapat melihat berbagai contoh fungsi sinus untuk memahami konsepnya sepenuhnya. Ia bahkan menjelaskan teorema sinus dan hubungan fungsi sinus dengan rasio trigonometri lainnya.
rumus fungsi sinus
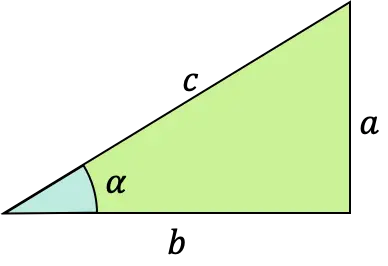
Fungsi sinus sudut α merupakan fungsi trigonometri yang rumusnya didefinisikan sebagai perbandingan antara kaki yang berhadapan dengan sisi miring suatu segitiga siku-siku (segitiga dengan sudut siku-siku).

Fungsi matematika jenis ini sering ditulis dengan singkatan “sin” atau “sin” (dari bahasa Latin sinus ). Selain itu, dapat juga disebut fungsi sinusoidal, sinusoidal, atau sinusoidal.
Fungsi sinus adalah salah satu perbandingan trigonometri yang paling terkenal, bersama dengan kosinus dan tangen suatu sudut.
Nilai karakteristik fungsi sinus
Beberapa sudut sering berulang dan oleh karena itu, akan lebih mudah untuk mengetahui nilai fungsi sinus pada sudut-sudut ini:
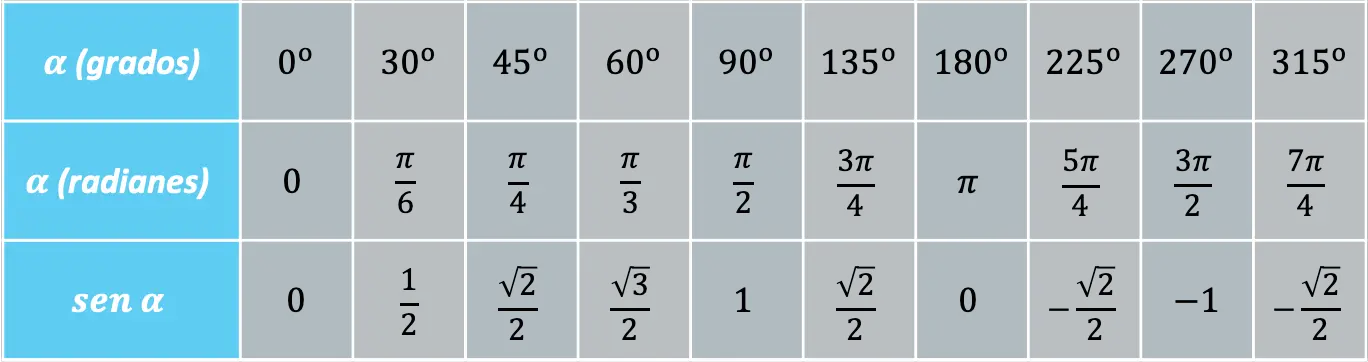
Jadi, tanda fungsi sinus bergantung pada kuadran dimana sudut tersebut berada: jika sudut berada pada kuadran pertama atau kedua maka sinusnya positif, sebaliknya jika sudut berada pada kuadran ketiga atau keempat. , sinusnya akan negatif.
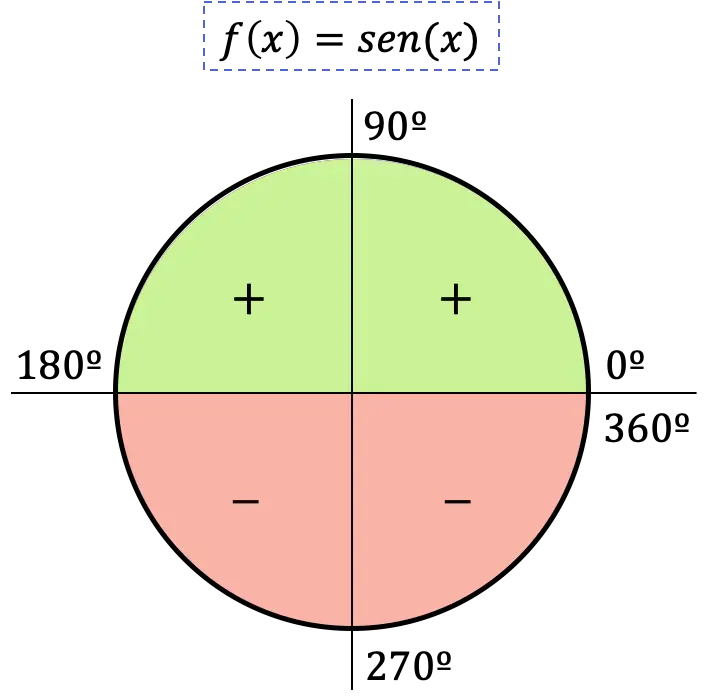
Representasi grafis dari fungsi sinus
Dengan tabel nilai yang kita lihat di bagian sebelumnya, kita dapat membuat grafik fungsi sinus. Jadi, ketika kita membuat grafik fungsi sinus, kita mendapatkan:
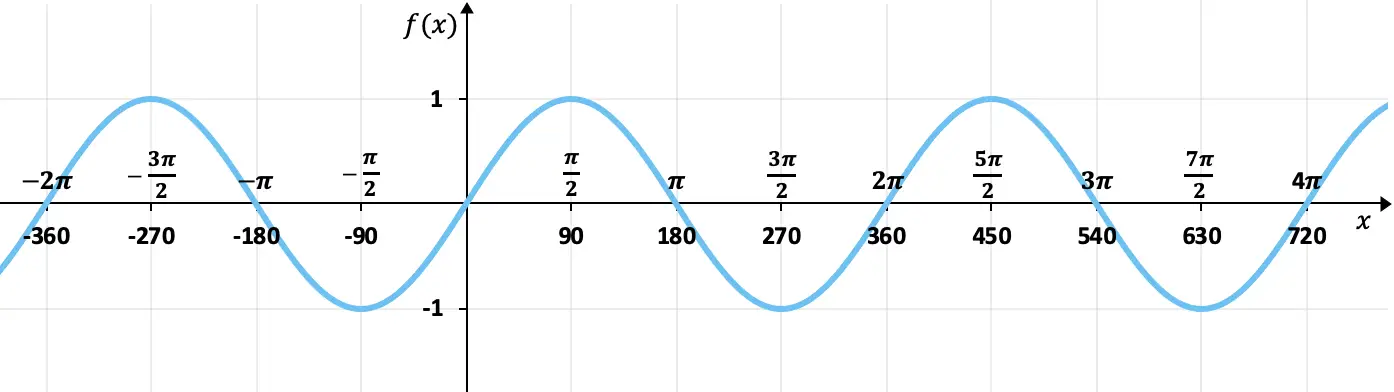
Terlihat dari grafik, nilai bayangan fungsi sinus selalu antara +1 dan -1, yaitu dibatasi di atas oleh +1 dan di bawah dibatasi oleh -1. Selain itu, nilainya diulang setiap 360 derajat (2π radian), sehingga merupakan fungsi periodik yang periodenya 360º.
Sebaliknya, pada grafik ini kita mengetahui dengan sempurna bahwa fungsi sinus adalah ganjil, karena elemen-elemen yang berlawanan memiliki bayangan yang berlawanan, atau dengan kata lain, simetris terhadap titik asal (0,0). Misalnya sinus 90º adalah 1 dan sinus -90º adalah -1.
Sifat-sifat fungsi sinus
Fungsi sinus mempunyai ciri-ciri sebagai berikut:
- Domain fungsi sinus adalah semua bilangan real karena, seperti yang ditunjukkan grafik, fungsi tersebut ada untuk sembarang nilai variabel bebas x.
![]()
- Jalur atau rentang fungsi sinus adalah dari minus 1 hingga plus 1 (keduanya inklusif).
![]()
- Ini adalah fungsi kontinu dan ganjil dengan periodisitas 2π.
![]()
- Fungsi trigonometri jenis ini memiliki satu titik potong dengan sumbu y (sumbu Y) di titik (0,0).
![]()
- Sebaliknya, ia secara berkala memotong absis (sumbu X) pada beberapa koordinat pi.
![]()
- Fungsi sinus maksimum terjadi ketika:
![]()
- Dan sebaliknya, fungsi sinus minimum terjadi pada:
![]()
- Turunan fungsi sinus adalah kosinus:
![]()
- Terakhir, integral fungsi sinus adalah tanda perubahan kosinus:
![]()
Periode dan amplitudo fungsi sinus
Seperti yang kita lihat pada grafiknya, fungsi sinus adalah fungsi periodik, yaitu nilainya berulang menurut frekuensi. Selain itu, nilai maksimum dan minimum di mana ia berosilasi bergantung pada amplitudonya. Oleh karena itu, dua ciri yang menentukan fungsi sinusoidal adalah periode dan amplitudonya:
![]()
- Periode fungsi sinus adalah jarak antara dua titik di mana grafik diulang dan dihitung dengan rumus berikut:
![]()
- Amplitudo fungsi sinus setara dengan koefisien di depan suku sinus.
![]()
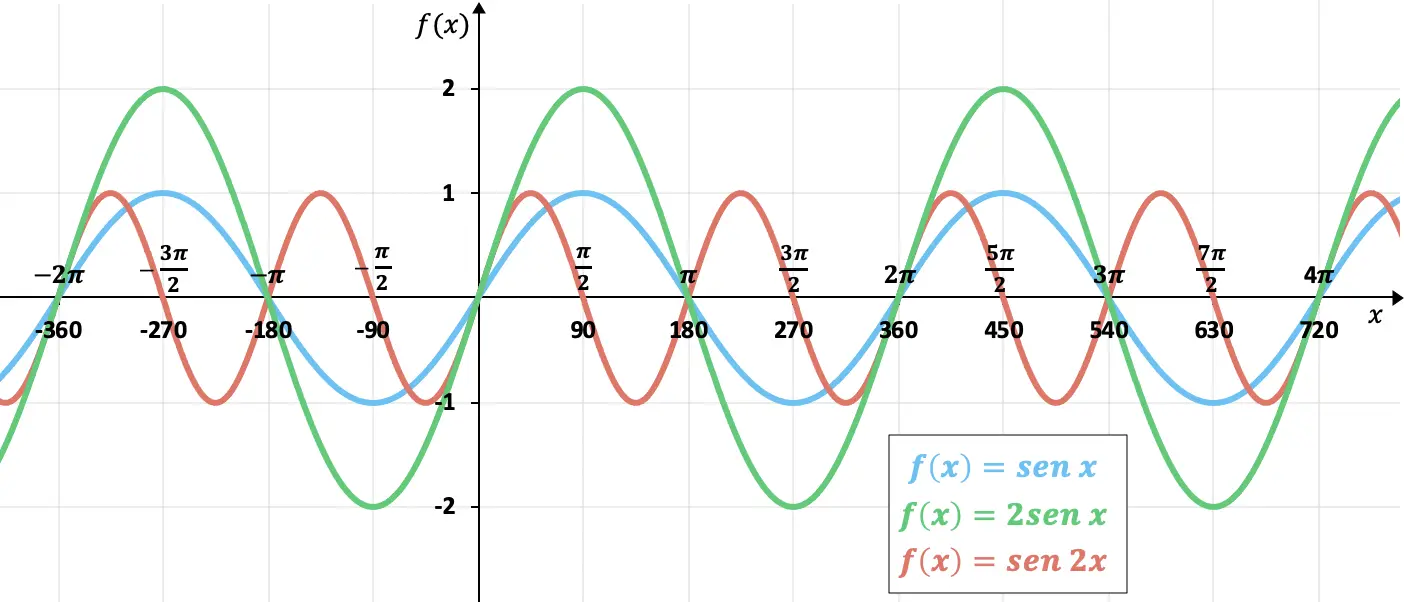
Di bawah ini Anda dapat melihat grafik yang menunjukkan pengaruh perubahan periode atau amplitudo:

Pada fungsi yang ditunjukkan dengan warna hijau, kita dapat melihat bahwa dengan menggandakan amplitudo, fungsinya berubah dari +2 ke -2, bukan +1 ke -1. Di sisi lain, dalam fungsi yang ditunjukkan dengan warna merah, Anda dapat melihat bagaimana fungsi ini berjalan dua kali lebih cepat dari fungsi sinus “kanonik”, karena periodenya telah dibelah dua.
teorema sinus
Meskipun sinus biasanya diterapkan pada segitiga siku-siku, ada juga teorema yang dapat digunakan untuk semua jenis segitiga: teorema sinus.
Hukum sinus menghubungkan sisi dan sudut suatu segitiga sebagai berikut:
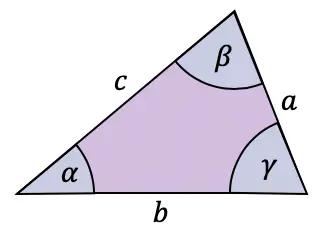
![]()
Hubungan fungsi sinus dengan perbandingan trigonometri lainnya
Di bawah ini Anda akan menemukan hubungan sinusoidal dengan rasio trigonometri terpenting dalam trigonometri.
Rasio kosinus
- Grafik fungsi cosinus ekuivalen dengan kurva sinus namun bergeser
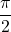
ke kiri, sehingga kedua fungsi tersebut dapat dihubungkan dengan ekspresi berikut:
![]()
- Anda juga dapat menghubungkan sinus dan kosinus dengan identitas dasar trigonometri:
![]()
kaitannya dengan garis singgung
- Meskipun pembuktiannya rumit, sinus hanya dapat dinyatakan berdasarkan garis singgung:
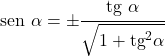
Hubungan dengan kosekan
- Sinus dan kosekan merupakan invers perkalian:
![]()
Hubungan dengan garis potong
- Sinusnya bisa dihapus sehingga hanya bergantung pada garis potongnya:
![]()
Hubungan dengan kotangen
- Sinus dan kotangen suatu sudut dihubungkan dengan persamaan berikut: