Matriks idempoten - Mathority

Pada halaman ini kami menjelaskan apa itu matriks idempoten. Kami juga menunjukkan beberapa contoh matriks jenis ini agar Anda memahaminya secara menyeluruh. Selain itu, Anda juga akan menemukan rumus untuk mencari matriks idempoten dan, terakhir, semua sifat matriks idempoten.

Apa yang dimaksud dengan matriks idempoten?

Pengertian matriks idempoten adalah sebagai berikut:

Matriks idempoten adalah matriks yang jika dikalikan dengan dirinya sendiri akan menghasilkan matriks yang sama.

$A\cdot A = A$

Oleh karena itu, pangkat apa pun dari matriks idempoten sama dengan matriks itu sendiri, berapapun eksponennya:

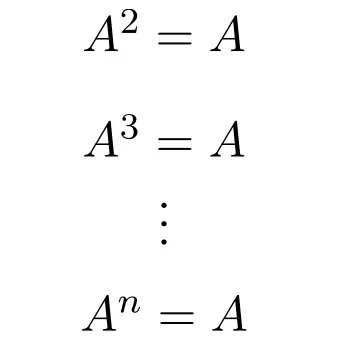
Faktanya, inilah mengapa papan jenis ini mendapatkan namanya. Karena dalam matematika, idempotensi merupakan operasi yang artinya kita selalu memperoleh hasil yang sama berapa kali pun dilakukan.

Contoh matriks idempoten

Setelah kita mengetahui konsep matriks idempoten, kita akan melihat beberapa contoh dimensi yang berbeda untuk menyelesaikan pemahamannya.

Contoh matriks idempoten 2×2

Matriks persegi berdimensi 2×2 berikut ini idempoten:

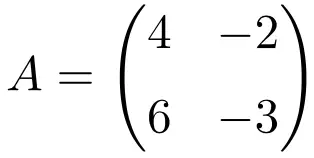
Untuk memverifikasi bahwa matriks tersebut merupakan matriks idempoten, kita menghitung kuadratnya:

$\displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}$

Hasilnya sama, sehingga dapat dibuktikan bahwa matriks tersebut merupakan matriks idempoten.

Contoh matriks idempoten 3×3

Matriks persegi berikut berukuran 3×3 adalah idempoten:

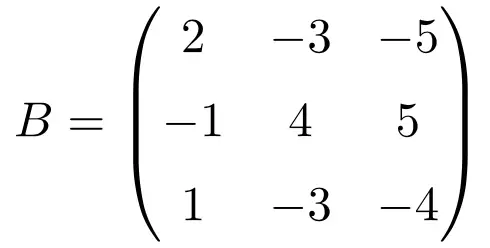
Untuk memeriksa kesesuaian matriks idempoten, kita menaikkan matriks menjadi 2:

$\displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}$

Hasilnya sama dengan matriks aslinya, sehingga idempotensi matriks tersebut terbukti.

Struktur matriks idempoten 2×2

Di sini kami tunjukkan rumus untuk mendapatkan matriks idempoten. Jika Anda lebih tertarik, Anda dapat melihat demonstrasi rumus di bawah ini di kolom komentar, namun agak membosankan, jadi berikut kami tinggalkan langsung rumus matriks idempoten :

Sedemikian rupa sehingga elemen-elemen diagonal sekunder suatu matriks idempoten dapat berubah-ubah selama syaratnya terpenuhi

$a^2+bc=a$

dan angka pada diagonal utama haruslah

$a$

Dan

$1-a.$

Selain semua matriks yang dijelaskan oleh rumus ini, kita harus menambahkan matriks Identitas, yang juga merupakan matriks idempoten meskipun tidak mengikuti rumus tersebut. Jika Anda tidak tahu apa itu array, Anda bisa bertanya apa itu array Identity .

Sifat-sifat matriks idempoten

Matriks idempoten mempunyai ciri-ciri sebagai berikut:

Penentu matriks idempoten selalu 0 atau 1.

Kecuali matriks identitas, semua matriks idempoten lainnya merupakan matriks tunggal atau matriks degenerasi, artinya matriks tersebut tidak dapat dibalik.

Setiap matriks idempoten dapat didiagonalisasi, dan nilai eigennya (atau nilai eigen) selalu 0 atau 1.

Jejak suatu matriks idempoten sama dengan pangkat matriks tersebut.

Terakhir, terdapat hubungan antara matriks idempoten dan matriks involusional: matriks
$A$

idempoten jika dan hanya jika matriksnya

$\displaystyle P= 2A-I$

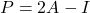
itu tidak disengaja.