Pada halaman ini kami menjelaskan apa itu matriks antisimetris. Selain itu, Anda akan dapat melihat beberapa contoh serta struktur khasnya untuk memahaminya dengan sempurna. Kami juga menjelaskan kekhasan penghitungan determinan matriks antisimetris dan semua sifat matriks jenis ini. Dan terakhir, Anda akan menemukan cara menguraikan matriks persegi apa pun menjadi jumlah matriks simetris ditambah matriks antisimetris lainnya.
Apa yang dimaksud dengan matriks antisimetris?
Pengertian matriks antisimetris adalah sebagai berikut:
Matriks antisimetris adalah matriks persegi yang transposnya sama dengan negatif matriksnya.
![]()
Emas
![]()
mewakili matriks yang ditransposisikan dari
![]()
Dan
![]()
adalah matriksnya
![]()
dengan semua elemennya berubah tanda.
Contoh matriks antisimetris
Setelah kita mengetahui konsep matriks antisimetri, kita akan melihat beberapa contoh matriks antisimetris untuk lebih memahaminya:
Contoh matriks antisimetri berorde 2×2
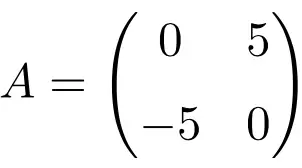
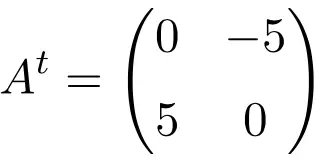
Contoh matriks antisimetris berdimensi 3×3
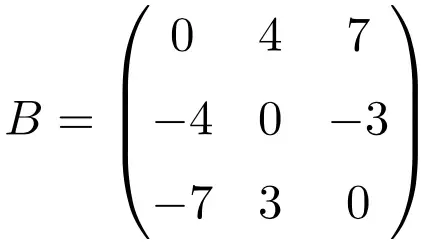
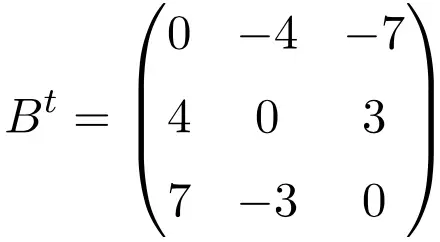
Contoh matriks antisimetris berukuran 4×4
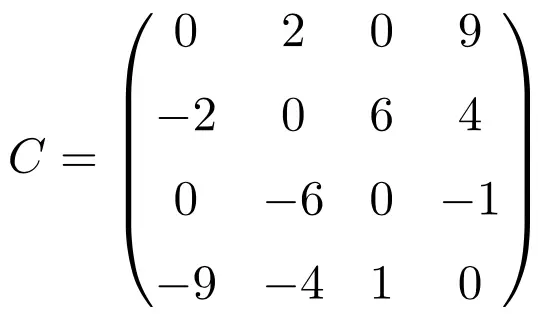
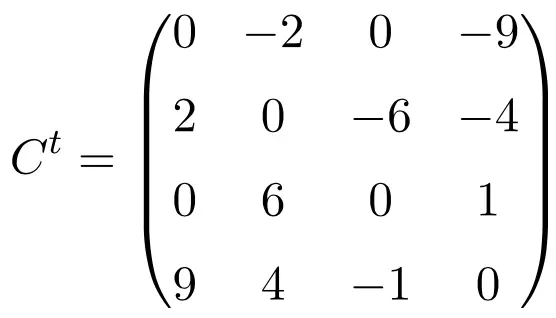
Saat melakukan transposisi ketiga matriks ini, kami memverifikasi bahwa ketiga matriks tersebut antisimetris, karena matriks yang ditransposisikan ekuivalen dengan matriks aslinya yang diubah tandanya.
Struktur matriks antisimetris
Agar syarat matriks antisimetris terpenuhi, matriks tersebut harus selalu mempunyai jenis struktur yang sama: bilangan-bilangan pada diagonal utama semuanya sama dengan nol dan elemen baris i dan kolom j adalah negatif elemen baris j dan kolom saya . Dengan kata lain, bentuk matriks antisimetrisnya adalah sebagai berikut:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 0 & a & b & \cdots & c\\[1.1ex]-a & 0 & d & \cdots &e\\[1.1ex]-b & -d & 0 & \cdots & f\\[1.1ex]\vdots & \vdots & \vdots & \ddots & \vdots\\[1.1ex] -c & -e & -f & \cdots & 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-21250d80d061affcf74ef1338b4d1314_l3.png)
Oleh karena itu, diagonal utama matriks antisimetri bertindak sebagai sumbu antisimetri. Dari sinilah nama matriks khusus ini berasal.
Penentu matriks antisimetris
Penentu matriks antisimetris bergantung pada dimensi matriks tersebut. Hal ini disebabkan oleh sifat-sifat determinan:
![]()
Jadi, jika matriks antisimetris berorde ganjil, determinannya sama dengan 0 . Sebaliknya, jika matriks antisimetris berdimensi genap, determinannya dapat bernilai berapa pun.
Oleh karena itu, matriks antisimetris berdimensi ganjil merupakan matriks tunggal atau matriks berdegenerasi. Sebaliknya, matriks antisimetri berorde genap adalah matriks beraturan.
Sifat-sifat matriks antisimetris
Ciri-ciri matriks antisimetri adalah sebagai berikut:
- Penjumlahan (atau pengurangan) dua matriks antisimetri menghasilkan matriks antisimetris lainnya. Karena mentransposisi dua matriks yang ditambah (atau dikurangi) sama dengan mentransposisi setiap matriks secara terpisah:
![]()
- Setiap matriks antisimetris yang dikalikan dengan suatu skalar juga akan menghasilkan matriks antisimetris yang lain.
- Kekuatan matriks antisimetri setara dengan matriks antisimetris atau matriks simetris. Jika eksponennya bilangan genap maka hasil pangkatnya adalah matriks simetris, tetapi jika pangkatnya ganjil maka hasil pangkatnya adalah matriks antisimetris. Anda dapat berkonsultasi di tautan ini apa itu matriks simetris .
- Jejak matriks antisimetris selalu sama dengan nol.
- Jumlah matriks antisimetri ditambah matriks kesatuan menghasilkan matriks yang dapat dibalik.
![]()
- Semua nilai eigen (atau nilai eigen) sebenarnya dari matriks antisimetris adalah 0. Namun, matriks antisimetris juga dapat memiliki nilai eigen yang kompleks.
- Semua matriks antisimetris adalah matriks normal. Oleh karena itu, mereka tunduk pada teorema spektral, yang mengatakan bahwa matriks antisimetris dapat didiagonalisasi oleh matriks kesatuan.
Penguraian matriks persegi menjadi matriks simetris dan matriks antisimetris
Ciri khusus matriks persegi adalah matriks tersebut dapat diuraikan menjadi jumlah matriks simetris ditambah matriks antisimetris.
Rumus yang memungkinkan kita melakukan hal ini adalah sebagai berikut:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3b9aa2b7ed0e9ce31587d4f00f1144e_l3.png)
Dimana C adalah matriks persegi yang ingin kita dekomposisi, C t transposnya, dan terakhir S dan A masing-masing adalah matriks simetris dan antisimetris yang menjadi tempat dekomposisi matriks C.
Di bawah ini Anda memiliki latihan yang diselesaikan untuk mendemonstrasikan rumusnya. Mari kita dekomposisi matriks berikut:
![Rendered by QuickLaTeX.com \displaystyle C=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5534c773c54b15eab3d0ab4a5823ce6c_l3.png)
Kita menghitung matriks simetris dan antisimetris dengan rumus:
![Rendered by QuickLaTeX.com \displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44ecbf11344f1de645aed313f801fa0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bc3c78415b6596b99186207efde54e7_l3.png)
Dan kita dapat memeriksa apakah persamaan tersebut terpenuhi dengan menjumlahkan kedua matriks:
![]()
![Rendered by QuickLaTeX.com \displaystyle\begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}+\begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2725b1e3a2de74b4446145ef32b61d1f_l3.png)
![]()
✅