Di halaman ini Anda akan menemukan penjelasan tentang apa itu matriks simetris. Selain itu, kami akan menunjukkan kepada Anda cara cepat mengidentifikasi suatu matriks simetris, beserta beberapa contohnya sehingga Anda tidak perlu ragu. Anda juga akan menemukan semua sifat matriks simetris. Dan terakhir, kami menjelaskan ciri khusus yang dimiliki oleh setiap matriks persegi: matriks tersebut dapat diuraikan menjadi jumlah matriks simetris dan matriks antisimetris.
Apa itu matriks simetris?
Pengertian matriks simetris adalah sebagai berikut:
Matriks simetris adalah matriks persegi yang transposnya sama dengan matriks itu sendiri.
![]()
Emas
![]()
mewakili matriks yang ditransposisikan dari
![]()
.
Setelah kita mengetahui konsep matriks simetris, kita akan melihat bagaimana matriks simetris dapat dengan mudah diidentifikasi:
Kapan suatu matriks simetris?
Mengenali struktur matriks simetris sangatlah sederhana: elemen baris i dan kolom j harus identik dengan elemen baris j dan kolom i . Dan nilai diagonal utama matriks dapat berupa apa saja.
Contoh matriks simetris
Berikut beberapa contoh matriks simetris untuk membantu Anda memahami:
Contoh matriks simetris berorde 2×2
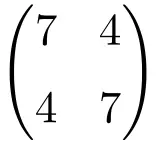
Contoh matriks simetris berdimensi 3×3

Contoh matriks simetris berukuran 4×4
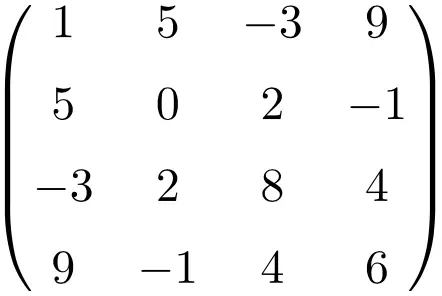
Dengan melakukan transposisi ketiga matriks ini kita memverifikasi bahwa matriks-matriks tersebut simetris, karena matriks-matriks yang ditransposisikan ekuivalen dengan matriks aslinya masing-masing.
Mengapa disebut matriks simetris?
Jika diperhatikan contoh sebelumnya, diagonal utama suatu matriks simetris adalah sumbu simetri, atau dengan kata lain bertindak sebagai cermin antara bilangan di atas diagonal dan bilangan di bawahnya. Oleh karena itu, matriks jenis ini disebut simetris.
Sifat-sifat matriks simetris
Ciri-ciri matriks simetris adalah sebagai berikut:
- Penjumlahan (atau pengurangan) dua matriks simetris menghasilkan matriks simetris lainnya. Karena mentransposisi dua matriks yang ditambah (atau dikurangi) sama dengan mentransposisi setiap matriks secara terpisah:
![]()
- Setiap matriks simetris yang dikalikan dengan skalar juga akan menghasilkan matriks simetris lainnya.
- Demikian pula hasil kali matriks antara dua matriks simetris tidak selalu sama dengan matriks simetris lainnya, hanya jika dan hanya jika kedua matriks tersebut dapat dikomutasi. Kondisi ini dapat dibuktikan dengan sifat perkalian matriks yang ditransposisikan:
![]()
- Pangkat suatu matriks simetris memunculkan matriks simetris lainnya, asalkan eksponennya bilangan bulat.
- Jelasnya, matriks kesatuan dan matriks nol merupakan contoh matriks simetris.
- Suatu matriks yang kongruen dengan matriks simetris juga harus simetris.
- Jika suatu matriks simetris beraturan atau dapat dibalik, maka matriks inversnya juga simetris.
- Begitu pula dengan adjoin matriks simetris: matriks adjoin dari matriks simetris menghasilkan matriks simetris lain sebagai solusinya.
- Matriks simetris sejati juga merupakan matriks normal.
- Karena matriks simetris merupakan kasus khusus dari matriks Hermitian, semua nilai eigen (atau nilai eigen) dari matriks simetris adalah bilangan real.
- Teorema spektral menyatakan bahwa semua matriks yang elemen-elemennya nyata adalah matriks yang dapat didiagonalisasi dan, terlebih lagi, diagonalisasi dilakukan melalui matriks ortogonal. Oleh karena itu, semua matriks simetris nyata didiagonalisasi secara ortogonal.
- Sebaliknya, matriks simetris dengan bilangan kompleks dapat didiagonalisasi melalui matriks kesatuan.
- Matriks Hessian selalu simetris.
Penguraian matriks persegi menjadi matriks simetris dan matriks antisimetris
Ciri khusus matriks persegi adalah matriks tersebut dapat diuraikan menjadi jumlah matriks simetris ditambah matriks antisimetris.
Rumus yang memungkinkan kita melakukan hal ini adalah sebagai berikut:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3b9aa2b7ed0e9ce31587d4f00f1144e_l3.png)
Dimana C adalah matriks persegi yang ingin kita dekomposisi, C t transposnya, dan terakhir S dan A masing-masing adalah matriks simetris dan antisimetris yang menjadi tempat dekomposisi matriks C.
Di bawah ini Anda memiliki latihan yang telah diselesaikan untuk melihat bagaimana hal ini dilakukan. Mari kita dekomposisi matriks berikut:
![Rendered by QuickLaTeX.com \displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-852a7267895a7f332ad3f28f8a8dda0d_l3.png)
Kita menghitung matriks simetris dan antisimetris dengan rumus:
![Rendered by QuickLaTeX.com \displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-994670ecc17b3bc8757482f1656e543e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d87e1d30d2bc657c20535f45c0fb7be6_l3.png)
Dan kita dapat memeriksa apakah persamaan tersebut terpenuhi dengan menjumlahkan kedua matriks:
![]()
![Rendered by QuickLaTeX.com \displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7cfdbffec6801c13041cd2996da13e96_l3.png)
![]()
✅