Pada artikel ini kami menjelaskan cara menurunkan fungsi (rumus). Anda juga akan menemukan contoh turunan pengurangan dan menyelesaikan latihan langkah demi langkah untuk berlatih.
Rumus turunan dari suatu pengurangan
Turunan dari pengurangan dua fungsi sama dengan mengurangkan turunan masing-masing fungsi secara terpisah.
![]()
Dengan kata lain, membedakan dua fungsi secara terpisah lalu mengurangkannya sama dengan mengurangkan fungsi terlebih dahulu lalu mengambil turunannya.
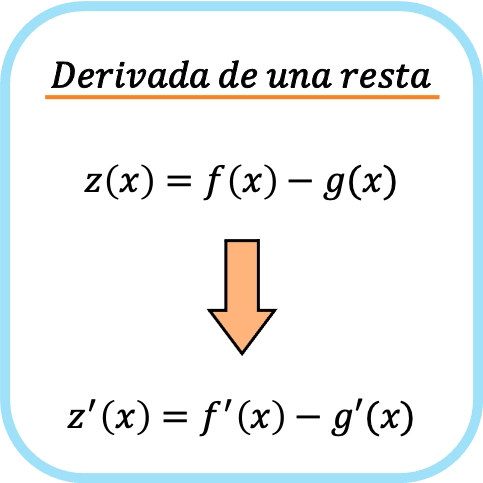
Demikian pula, aturan diferensiasi yang sama berlaku untuk pengurangan dua fungsi atau lebih, jadi jika kita melakukan pengurangan tiga, empat, lima,… fungsi, kita perlu membedakan masing-masing fungsi secara terpisah lalu mengurangkannya.
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bc282473a7f7560eebc97db66bb8f54_l3.png)
Seperti yang Anda lihat, rumus turunan selisih fungsi sangat mirip dengan aturan turunan suatu penjumlahan.
➤ Lihat: turunan dari sejumlah fungsi
Contoh turunan dari pengurangan
Setelah kita mengetahui rumus turunan dari suatu pengurangan, sekarang kita beralih ke menganalisis beberapa contoh turunan dari jenis operasi ini untuk memahami sepenuhnya bagaimana pengurangan suatu fungsi diturunkan.
Contoh 1: Turunan dari pengurangan fungsi potensial
![]()
Turunan pengurangan dua fungsi sama dengan selisih turunan masing-masing fungsi secara terpisah. Oleh karena itu, pertama-tama kita akan menghitung turunan setiap fungsi secara terpisah:
![]()
![]()
Oleh karena itu, turunan dari seluruh fungsi adalah sebagai berikut:
![]()
Contoh 2: Turunan dari pengurangan fungsi yang berbeda
![]()
Untuk membedakan fungsi pengurangan, pertama-tama Anda harus membedakan kedua fungsi tersebut secara terpisah, lalu mengurangkannya.
![]()
![]()
Dan setelah membuat kedua turunannya, kita kurangi dengan orde awal yang sama:
![]()
Contoh 3: Turunan dari pengurangan kuadrat
![]()
Dalam hal ini kita mempunyai fungsi komposit, karena merupakan pengurangan antara tiga fungsi kuadrat. Oleh karena itu kita harus menggunakan rumus turunan suatu fungsi potensial dan aturan rantai untuk menghitung turunan seluruh fungsi:
![]()
➤ Lihat: rumus turunan suatu pangkat
Latihan soal turunan pengurangan
Turunkan pengurangan fungsi berikut:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Bukti turunan dari suatu pengurangan
Selanjutnya kita akan mendemonstrasikan rumus turunan pengurangan fungsi dari definisi turunan, yaitu:
![]()
Jadi jika z adalah selisih dua fungsi berbeda:
![]()
![]()
Kita mengganti z dengan pengurangan fungsi dalam ekspresi limit:
![]()
![]()
Sekarang kita akan melakukan transformasi untuk memisahkan pecahan dan memperoleh pengurangan dua pecahan:
![]()
![]()
Dengan menerapkan hukum limit, kita dapat memisahkan persamaan di atas menjadi dua limit yang berbeda. Karena limit suatu pengurangan sama dengan pengurangan limit:
![]()
Jika diperhatikan lebih dekat, setiap limit berhubungan dengan turunan suatu fungsi, yang berarti rumus turunan selisih terpenuhi:
![]()