Di halaman ini Anda akan melihat apa yang dimaksud dengan matriks menjadi tunggal atau berdegenerasi. Selain itu, kami tunjukkan beberapa contoh agar Anda tidak ragu dan terakhir, kami menjelaskan semua properti matriks jenis ini.
Apa yang dimaksud dengan matriks tunggal atau matriks degenerasi?
Pengertian matriks singular disebut juga matriks degenerasi adalah sebagai berikut:
Matriks tunggal atau matriks berdegenerasi adalah matriks persegi yang tidak dapat dibalik sehingga determinannya sama dengan 0.
Jadi, untuk mengetahui suatu matriks tunggal, cukup hitung determinannya: jika hasilnya 0 maka matriksnya tunggal, sebaliknya jika determinannya berbeda dengan 0 maka matriksnya tidak tunggal. .
Jika Anda ingin mengetahui lebih banyak tentang matriks invers, Anda dapat membaca halaman ini yang menjelaskan secara rinci cara membalikkan matriks menggunakan metode Gauss , Anda juga akan menemukan beberapa contoh dan latihan yang diselesaikan langkah demi langkah untuk latihan.
Di sisi lain, matriks tunggal disebut juga matriks tak beraturan, karena matriks tersebut merupakan kebalikan dari matriks beraturan .
Contoh matriks tunggal
Setelah kita melihat penjelasan tentang matriks singular atau matriks degenerasi, mari kita lihat beberapa contoh matriks singular dengan beberapa dimensi:
Contoh matriks singular 2×2
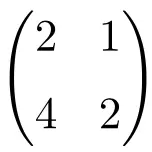
Kita dapat dengan mudah memverifikasi bahwa ini adalah matriks tunggal dengan menghitung determinannya:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 2&1 \\[1.1ex] 4 & 2\end{vmatrix}\bm{=0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e8466c3a7108986306c5e06a6b49049_l3.png)
Penentu matriks orde 2 sama dengan 0, sehingga merupakan matriks singular.
Contoh matriks tunggal 3×3
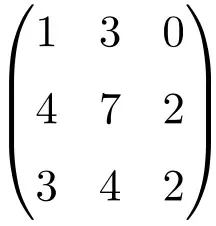
Kita harus menyelesaikan determinan matriks tersebut untuk memverifikasi bahwa matriks tersebut adalah matriks yang tidak dapat dibalik:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1&3&0\\[1.1ex] 4&7&2\\[1.1ex] 3&4&2\end{vmatrix}\bm{=0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1aebdc318be6773a6d4d78e9fcedaf5d_l3.png)
Penentu matriks berorde 3 menghasilkan 0, sehingga matriks tersebut merupakan matriks singular.
Contoh matriks tunggal 4×4
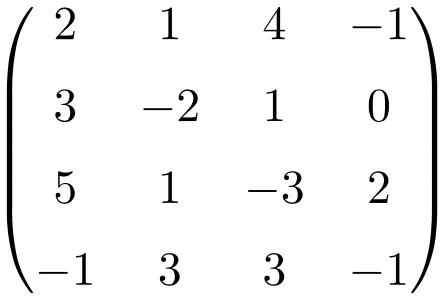
Dengan membuat determinan dari matriks tersebut kita menunjukkan bahwa matriks tersebut adalah matriks singular:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 2&1&4&-1\\[1.1ex] 3&-2&1&0\\[1.1ex] 5&1&-3&2\\[1.1ex] -1&3&3&-1\end{vmatrix}\bm{=0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ad6c7444321a65bb993c2abc87f93a0_l3.png)
Penentu matriks berorde 4 adalah nol, sehingga inversnya tidak ada.
Peringatan: Jika Anda ragu dengan perhitungan determinan, Anda dapat membaca halaman cara menghitung determinan .
Sifat-sifat matriks tunggal
Ciri-ciri matriks jenis ini adalah sebagai berikut:
- Setidaknya dua kolom atau dua baris matriks tunggal merupakan kombinasi linier dan oleh karena itu bersifat linier bergantung.
- Matriks apa pun yang baris atau kolomnya berisi nol merupakan matriks singular.
- Pangkat suatu matriks tunggal atau matriks yang mengalami degenerasi lebih kecil dari ukurannya.
- Hasil kali matriks suatu matriks tunggal dikalikan dengan matriks lainnya menghasilkan matriks tunggal lainnya. Kondisi ini dapat disimpulkan dari sifat-sifat determinannya:
![]()
- Demikian pula, pangkat suatu matriks tunggal sama dengan matriks tunggal lainnya, berapa pun pangkat yang dipangkatkannya.
- Transpos suatu matriks singular menimbulkan matriks singular lainnya, karena determinan matriks yang ditransposisikan (atau ditransposisikan) setara dengan determinan matriks yang tidak ditransposisikan:
![]()
- Mengalikan matriks singular dengan skalar tidak mengubah statusnya sebagai matriks yang mengalami degenerasi.
- Adjoint suatu matriks singular juga bersifat singular.
- Matriks segitiga dan matriks diagonal adalah matriks berdegenerasi jika paling sedikit salah satu elemen diagonal utamanya adalah nol.
- Jelasnya, matriks nol merupakan matriks singular.
- Dengan cara yang sama, matriks nilpoten juga merupakan matriks tunggal.
- Suatu sistem persamaan linier yang dihubungkan dengan matriks tunggal tidak mempunyai penyelesaian atau mempunyai banyak penyelesaian yang tak terhingga.
- Terakhir, matriks persegi dikatakan tunggal jika dan hanya jika matriks tersebut mempunyai paling sedikit satu nilai eigen (atau nilai eigen) yang sama dengan 0.