Matriks ortogonal - Mathoritas

Di halaman ini Anda akan melihat apa itu matriks ortogonal dan hubungannya dengan invers suatu matriks. Anda juga akan melihat beberapa contoh untuk memahaminya dengan sempurna. Selain itu, kami mengajari Anda rumus yang memeriksa matriks ortogonal apa pun, yang dengannya Anda akan mengetahui cara menemukannya dengan cepat. Dan terakhir, Anda akan menemukan properti dan penerapan matriks khusus ini serta latihan ujian yang diselesaikan secara umum.

Apa itu matriks ortogonal?

Pengertian matriks ortogonal adalah sebagai berikut:

Matriks ortogonal adalah matriks bilangan real persegi yang dikalikan transposnya (atau transposnya) sama dengan matriks identitas. Artinya, kondisi berikut terpenuhi:

$A\cdot A^t = A^t \cdot A =I$

Emas

$A$

adalah matriks ortogonal dan

$A^t$

mewakili matriks yang ditransposisikan.

Agar kondisi ini terpenuhi, kolom dan baris matriks ortogonal harus merupakan vektor satuan ortogonal, yaitu harus membentuk basis ortonormal. Oleh karena itu, beberapa ahli matematika juga menyebutnya matriks ortonormal .

Kebalikan dari matriks ortogonal

Cara lain untuk menjelaskan konsep matriks ortogonal adalah melalui matriks invers, karena transpos (atau transpos) matriks suatu matriks ortogonal sama dengan inversnya.

Untuk memahami teorema ini sepenuhnya, penting bagi Anda untuk mengetahui cara membalikkan matriks . Di tautan ini Anda akan menemukan penjelasan mendetail tentang invers matriks, semua propertinya, dan Anda bahkan memiliki latihan penyelesaian langkah demi langkah untuk dipraktikkan.

Matriks invers suatu matriks ortogonal dapat dengan mudah ditunjukkan ekuivalennya dengan transposnya menggunakan kondisi matriks ortogonal dan sifat utama matriks invers:

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

Oleh karena itu, matriks ortogonal akan selalu merupakan matriks yang dapat dibalik , atau dengan kata lain matriks beraturan atau matriks tak berdegenerasi.

Selanjutnya kita akan melihat beberapa contoh matriks ortogonal untuk melengkapi pemahaman konsep segala sesuatu.

Contoh matriks ortogonal 2×2

Matriks berikut merupakan matriks ortogonal berdimensi 2×2:

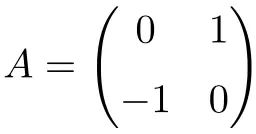
Kita dapat memeriksa ortogonalnya dengan menghitung hasil kali berdasarkan transposnya:

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Karena hasilnya menghasilkan matriks Identik, kita verifikasi bahwa A adalah matriks ortogonal.

Contoh matriks ortogonal 3×3

Matriks berikut merupakan matriks ortogonal berdimensi 3×3:

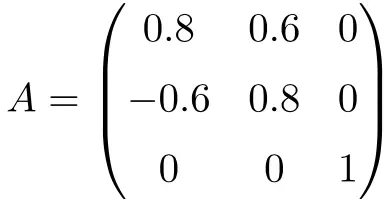
Kita dapat menunjukkan bahwa matriks tersebut ortogonal dengan mengalikan matriks A dengan transposnya:

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

Karena penyelesaiannya adalah matriks kesatuan, kita tunjukkan bahwa A adalah matriks ortogonal.

Rumus mencari matriks ortogonal 2×2

Kita kemudian akan melihat bukti bahwa semua matriks ortogonal orde 2 mengikuti pola yang sama.

Pertimbangkan matriks generik berukuran 2×2:

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

Agar matriks ini ortogonal, persamaan matriks berikut harus dipenuhi:

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Menyelesaikan perkalian matriks, kita memperoleh persamaan berikut:

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

Jika Anda perhatikan lebih dekat, persamaan ini sangat mirip dengan hubungan dasar trigonometri Pythagoras :

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

Oleh karena itu, suku-suku yang memenuhi persamaan (1) dan (3) yang diperoleh adalah:

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

Selain itu, dengan mensubstitusikan nilai-nilai tersebut ke dalam persamaan kedua, kita memperoleh hubungan antara kedua sudut:

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

Artinya, salah satu dari dua syarat berikut harus dipenuhi:

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

Jadi, kesimpulannya, matriks ortogonal harus mempunyai struktur salah satu dari dua matriks berikut:

Emas

$\theta$

adalah bilangan real.

Memang kalau sebagai contoh kita memberi nilai

$\displaystyle\theta=\frac{\pi}{2}$

dan kita ambil struktur pertama, kita akan memperoleh matriks yang telah kita verifikasi ortogonalnya pada bagian “Contoh matriks ortogonal 2×2”:

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

Properti Matriks Ortogonal

Ciri-ciri matriks jenis ini adalah:

Matriks ortogonal tidak akan pernah menjadi matriks tunggal karena matriks tersebut selalu dapat dibalik. Dalam pengertian ini, kebalikan dari matriks ortogonal adalah matriks ortogonal lainnya.

Matriks ortogonal apa pun dapat didiagonalisasi. Kita kemudian mengatakan bahwa matriks ortogonal dapat didiagonalisasi secara ortogonal.

Semua nilai eigen atau nilai eigen suatu matriks ortogonal mempunyai modulus sama dengan 1.

Matriks ortogonal apa pun yang hanya terdiri dari bilangan real juga merupakan matriks normal.

Analog dari matriks ortogonal dalam lingkungan dengan bilangan kompleks adalah matriks kesatuan.

Jelasnya matriks identitas merupakan matriks ortogonal.

Himpunan matriks ortogonal berdimensi n × n serta operasi hasil kali matriksnya membentuk suatu grup yang disebut grup ortogonal. Artinya, hasil kali dua matriks ortogonal sama dengan matriks ortogonal lainnya.

Selain itu, hasil perkalian matriks ortogonal dengan transposnya dapat dinyatakan dengan delta Kronecker:

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

Terakhir, determinan matriks ortogonal selalu +1 atau -1.

$\displaystyle \text{det}(A)=\pm 1$

Latihan matriks ortogonal yang diselesaikan

Selanjutnya kita akan menyelesaikan latihan matriks ortogonal.

Diketahui matriks persegi berorde 3 berikut, tentukan nilai dari
$a$

Dan

$b$

untuk membuatnya ortogonal:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

Agar ortogonalitas matriks terpenuhi, hasil kali matriks dengan transposnya harus sama dengan matriks Identitas. JADI:

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

Kami mengalikan matriks:

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$

Sekarang kita dapat memperoleh persamaan dari pojok kiri atas matriks, karena elemen-elemen pada posisi tersebut harus cocok. Belum:

$\displaystyle \frac{1}{9}(2a^2+1) = 1$

Kami memecahkan persamaan dan menghilangkan yang tidak diketahui:

$\displaystyle 2a^2+1 = 9$

$\displaystyle 2a^2 = 8$

$\displaystyle a^2 = 4$

$\displaystyle \bm{a = \pm 2}$

Namun, ada persamaan yang tidak berlaku untuk solusi positif, misalnya persamaan di pojok kanan atas. Jadi hanya solusi negatif yang mungkin dilakukan .

Di sisi lain, untuk menghitung variabel

$b$

kita dapat mencocokkan, misalnya, suku-suku yang ditempatkan pada baris kedua kolom pertama:

$\displaystyle \frac{1}{9}(ab+a+b) = 0$

$\displaystyle ab+a+b = 0$

Dengan mengganti nilai

$a$

dalam persamaan:

$\displaystyle -2b-2+b = 0$

$\displaystyle -b =2$

$\displaystyle \bm{b =-2}$

Singkatnya, satu-satunya solusi yang mungkin adalah:

$\displaystyle \bm{a=b =-2}$

Jadi matriks ortogonal yang sesuai dengan nilai-nilai ini adalah:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}$

Penerapan matriks ortogonal

Walaupun kelihatannya tidak begitu karena biasanya bentuknya sangat sederhana, matriks ortogonal sangat penting dalam matematika, khususnya dalam bidang aljabar linier.

Dalam geometri, matriks ortogonal mewakili transformasi isometrik (yang tidak mengubah jarak dan sudut) dalam ruang vektor nyata, oleh karena itu disebut transformasi ortogonal. Lebih lanjut, transformasi ini merupakan isomorfisme internal dari ruang vektor yang dipertimbangkan. Transformasi ini dapat berupa rotasi , refleksi specular , atau inversi .

Terakhir, matriks jenis ini juga digunakan dalam fisika, karena memungkinkan mempelajari pergerakan benda tegar. Dan mereka bahkan digunakan dalam perumusan teori lapangan tertentu.