Di sini kami menjelaskan apa rumus identitas penting dari kuadrat selisih (atau pengurangan), yaitu, kami menunjukkan kepada Anda bagaimana persamaan (ab) 2 diselesaikan. Selain itu, Anda akan dapat melihat contoh dan latihan dengan latihan yang diselesaikan pada kuadrat selisih. Dan terakhir, kami menunjukkan demonstrasi formula dan interpretasi geometris dari jenis produk yang luar biasa ini.
Berapakah kuadrat selisih (atau pengurangan)?
Kuadrat selisih , atau kuadrat pengurangan , adalah salah satu identitas penting (atau hasil kali penting), yaitu terdiri dari aturan matematika yang memfasilitasi penghitungan kuadratur binomial dengan dua suku: satu positif dan negatif lainnya.
Oleh karena itu, persamaan aljabar kuadrat selisih adalah (ab) 2 .
Rumus kuadrat selisih (atau pengurangan)
Setelah kita melihat definisi dari jenis identitas luar biasa ini, kita akan melihat cara menyelesaikan kuadrat selisih dengan rumusnya:

Sehingga kuadrat selisih sama dengan kuadrat suku pertama, dikurangi dua kali hasil kali suku pertama dan suku kedua, ditambah kuadrat suku kedua.
Jadi, untuk menghitung selisih atau pengurangan kuadrat, Anda tidak hanya harus menaikkan setiap suku menjadi dua, tetapi juga mengalikannya dengan 2.
Hal ini penting untuk diingat, karena kesalahan yang sangat umum saat melakukan pengurangan kuadrat adalah tidak meletakkan hasil kali di antara dua suku dan hanya menyelesaikan kuadrat pengurangan dan pengurangan dari pengurangan tersebut:

Jangan lupa hasil perkalian antara a dan b!
Contoh selisih (atau pengurangan) kuadrat
Sekarang setelah kita mengetahui rumus kuadrat selisih, kita dapat melakukan perhitungan dengannya. Agar Anda dapat melihat bagaimana hal ini dilakukan, kami telah menyiapkan beberapa contoh penyelesaian kuadrat selisih (atau pengurangan).
Contoh 1
- Selesaikan kuadrat selisih berikut:
![]()
Ini adalah pengurangan kuadrat, jadi Anda harus menerapkan rumusnya:
![]()
Jadi, kita harus mengidentifikasi apa saja nilai-nilai yang tidak diketahui
![]()
Dan
![]()
dari rumus tersebut. Pada kasus ini,
![]()
adalah variabelnya
![]()
Dan
![]()
sesuai dengan nomor 3:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1bb2d14a30d2cdabae6458f5df32392a_l3.png)
Perhatikan bahwa tanda negatif bukan bagian dari
![]()
tetapi Anda harus selalu mengambil angka tanpa tanda agar dapat menerapkan rumus dengan benar.
Oleh karena itu kita sudah mengetahui nilai-nilai
![]()
dan dari
![]()
Oleh karena itu, kita hanya perlu mensubstitusikan nilai-nilai ini ke dalam rumus:

Contoh 2
- Hitung binomial pengurangan kuadrat berikut:
![]()
Rumus selisih kuadrat adalah:
![]()
Jadi, pertama-tama kita perlu mengidentifikasi nilai-nilai
![]()
dan dari
![]()
dari rumus tersebut. Dalam masalah ini,
![]()
mewakili monomial
![]()
Dan
![]()
setara dengan suku bebas binomial, yaitu 2:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (5x-2)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=5x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-868a41eb665f5bc94959448547c060d5_l3.png)
Terakhir, setelah kita mengetahui nilai parameternya
![]()
Dan
![]()
, kita cukup menerapkan rumus binomial untuk pengurangan kuadrat:
![Rendered by QuickLaTeX.com \begin{aligned} (5x-2)^2 & = (5x)^2-2\cdot 5x \cdot 2 + 2^2 \\[2ex] & = 25x^2-20x+4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5e88231a654b23a306e53e17d175d25_l3.png)
Bukti rumus kuadrat selisih
Selanjutnya kita akan menyimpulkan dari mana rumus kuadrat pengurangan berasal. Meskipun Anda tidak perlu menghafal buktinya, tetap menyenangkan untuk memahami matematika di baliknya.
Jika kita mulai dari ekspresi binomial semua pengurangan:
![]()
Jelasnya, pangkat sebelumnya sama dengan hasil kali faktornya
![]()
dikalikan dengan dirinya sendiri:
![]()
Sekarang kita mengalikan kedua tanda kurung dengan menerapkan sifat distributif:
![Rendered by QuickLaTeX.com \begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b46073fd758d93fff8956f0a8dd57af_l3.png)
Dan kita hanya perlu mengelompokkan suku-suku serupa untuk menyelesaikan pembuktian rumusnya:
![]()
Agar rumus kuadrat pengurangan dapat dibuktikan secara matematis:
![]()
Yang menarik, perluasan ekspresi binomial dari pengurangan kuadrat juga dikenal sebagai trinomial kuadrat sempurna.
Interpretasi geometris dari kuadrat suatu perbedaan
Untuk menyelesaikan pemahaman tentang gagasan kuadrat suatu perbedaan, kita akan melihat bagaimana menafsirkan persamaan yang luar biasa ini secara geometris.
Perhatikan persegi berikut yang panjang sisi-sisinya
![]()
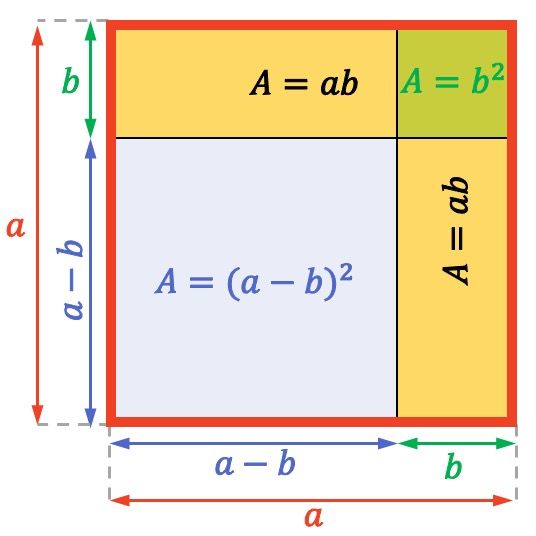
Luas (atau luas permukaan) persegi atau persegi panjang dihitung dengan mengalikan dua sisi yang berdekatan. Jadi, luas seluruh persegi bilangan bulat di atas adalah
![]()
Demikian pula luas setiap persegi panjang berwarna kuning adalah sama
![]()
Dan terakhir, persegi kecil di kanan atas mempunyai luas
![]()
Artinya persegi dengan sisinya
![]()
yang permukaannya
![]()
dapat diuraikan menjadi luas persegi berdimensi
![]()
dikurangi 2 kali luas persegi panjang
![]()
Dan
![]()
, ditambah luas sisi persegi
![]()
Singkatnya, rumus kuadrat selisih juga dapat diverifikasi secara geometris:
![]()
Menyelesaikan masalah kuadrat selisih (atau pengurangan)
Agar Anda dapat berlatih, kami memberikan kepada Anda beberapa latihan yang diselesaikan selangkah demi selangkah pada hasil kali kuadrat selisih yang penting. Ingatlah bahwa Anda dapat menulis kepada kami pertanyaan apa pun yang Anda miliki di bawah di komentar.
Latihan 1
Selesaikan pengurangan kuadrat berikut:
![]()
![]()
![]()
![]()
![]()
Untuk menemukan semua identitas masalah yang luar biasa, cukup menerapkan rumus kuadrat selisih, yaitu:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14d502eda968fe82617b4403cd9c4722_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c22d520301280872e645f5683a2fba8e_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95c7c481a96b20b700bd2253c90f0c0d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cea9fa89580d3d9d9df7fd93cca2b89_l3.png)
![Rendered by QuickLaTeX.com \text{E)} \ \begin{aligned}(4x-3y)^2 & = (4x)^2-2\cdot 4x\cdot 3y +(3y)^2\\[2ex] & = \bm{16x^2-24xy+9y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-138b359ce2e8f8b1012c6ecf1b7fb9b0_l3.png)
Latihan 2
Tentukan kuadrat selisih dua besaran berikut dengan menggunakan rumus:
![]()
![]()
![]()
Untuk menentukan semua hasil kali penting dari soal tersebut, perlu menggunakan rumus pengurangan kuadrat:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2\\[2ex] & = \bm{36x^6-48x^3y^4+16y^8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c73b9ba584f955a0cae5564a2226d465_l3.png)
Untuk menyelesaikan bagian B), perlu diingat bahwa jika suatu akar dikuadratkan, maka disederhanakan:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38cd9e9855f7f79f607247ccc731e297_l3.png)
Monomial pengurangan kuadrat terakhir mempunyai koefisien pecahan, jadi untuk menyelesaikannya kita perlu menggunakan sifat-sifat pecahan:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2 & = \left(\frac{5}{2}x^2\right)^2-2\cdot \frac{5}{2}x^2\cdot \frac{4}{5}x +\left(\frac{4}{5}x\right)^2\\[2ex] & = \frac{5^2}{2^2}x^4-2\cdot \frac{20}{10}x^3 +\frac{4^2}{5^2}x^2 \\[2ex] &= \frac{25}{4}x^4 -2\cdot 2x^3+\frac{16}{25}x^2 \\[2ex] & = \mathbf{\frac{25}{4}} \bm{x^4-4x^3+}\mathbf{\frac{16}{25}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-46106420913cc7a370e2f5215af0f2a2_l3.png)