Di halaman ini Anda akan menemukan apa itu matriks Jacobian dan cara menghitungnya menggunakan contoh. Selain itu, Anda memiliki beberapa latihan matriks Jacobian yang telah diselesaikan sehingga Anda dapat berlatih. Anda juga akan melihat mengapa determinan matriks Jacobian, Jacobian, sangat penting. Terakhir, kami menjelaskan hubungan yang dipertahankan matriks ini dengan operasi lain dan aplikasi yang dimilikinya.
Apa yang dimaksud dengan matriks Jacobian?
Pengertian matriks Jacobian adalah sebagai berikut:
Matriks Jacobian adalah matriks yang dibentuk oleh turunan parsial suatu fungsi orde pertama.
Oleh karena itu, rumus matriks Jacobian adalah sebagai berikut:

Oleh karena itu, matriks Jacobian akan selalu memiliki baris sebanyak fungsi skalar
![]()
memiliki fungsi, dan jumlah kolom akan sesuai dengan jumlah variabel
![]()
Di sisi lain, matriks ini juga dikenal sebagai peta diferensial Jacobian atau peta linier Jacobian . Bahkan terkadang juga ditulis dengan huruf D bukan huruf J:
![]()
Sebagai rasa ingin tahu, matriks Jacobian dinamai Carl Gustav Jacobi, seorang matematikawan dan profesor penting abad ke-19 yang memberikan kontribusi penting bagi dunia matematika, khususnya di bidang aljabar linier.
Contoh penghitungan matriks Jacobian
Setelah kita melihat konsep matriks Jacobian, kita akan melihat langkah demi langkah cara menghitungnya menggunakan contoh:
- Tentukan matriks Jacobian pada titik (1,2) dari fungsi berikut:
![]()
Hal pertama yang perlu kita lakukan adalah menghitung semua turunan parsial orde pertama dari fungsi tersebut:
![]()
![]()
![]()
![]()
Sekarang kita terapkan rumus matriks Jacobian. Dalam hal ini fungsi tersebut memiliki dua variabel dan dua fungsi skalar, sehingga matriks Jacobian akan menjadi matriks persegi berdimensi 2×2:
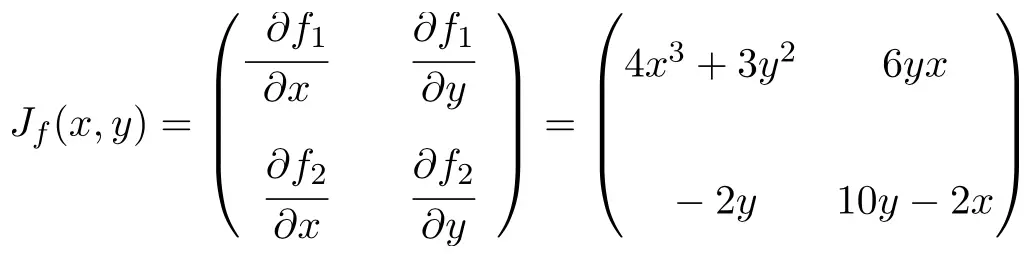
Setelah kita mendapatkan ekspresi untuk matriks Jacobian, kita mengevaluasinya pada titik (1,2):
![Rendered by QuickLaTeX.com \displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fa6ed35890b94e3abe43b9a3f9674e36_l3.png)
Dan akhirnya, kami melakukan operasi dan mendapatkan solusinya:
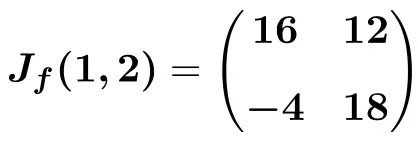
Setelah Anda melihat cara mencari matriks Jacobian suatu fungsi, kami memberikan beberapa latihan yang diselesaikan selangkah demi selangkah sehingga Anda dapat berlatih.
Memecahkan masalah matriks Jacobian
Latihan 1
Carilah matriks Jacobian di titik (0,-2) fungsi vektor berikut pada 2 variabel:
![]()
Fungsi tersebut memiliki dua variabel dan dua fungsi skalar, sehingga matriks Jacobian akan menjadi matriks persegi berukuran 2×2:
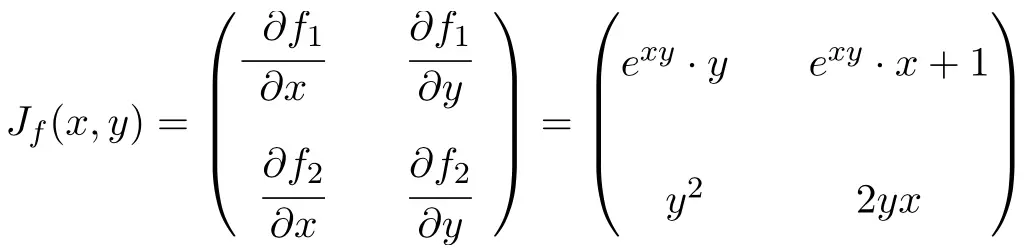
Setelah kita menghitung ekspresi matriks Jacobian, kita mengevaluasinya pada titik (0,-2):
^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4f6008d8799a0a1c3a667e958d6c8818_l3.png)
Dan akhirnya, kami melakukan operasi dan mendapatkan hasilnya:
![Rendered by QuickLaTeX.com \displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5eb37dc494497a424b489235b1a55a5f_l3.png)
Latihan 2
Hitung matriks Jacobian di titik (2,-1) fungsi berikut dengan 2 variabel:
![]()
Dalam hal ini fungsi tersebut memiliki dua variabel dan dua fungsi skalar, sehingga matriks Jacobian akan menjadi matriks persegi berorde 2:
![Rendered by QuickLaTeX.com \displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-48baf447fc5a448f30f13295f96cb874_l3.png)
Setelah kita menemukan ekspresi matriks Jacobian, kita evaluasinya pada titik (2,-1):
![Rendered by QuickLaTeX.com \displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4f2ee2de8e72eed6956f784628353547_l3.png)
Dan akhirnya, kami melakukan operasi dan mendapatkan hasilnya:
![Rendered by QuickLaTeX.com \displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7935318698eadf3d3af4f87e6e8f2629_l3.png)
Latihan 3
Tentukan matriks Jacobian di titik (2,-2,2) fungsi berikut dengan 3 variabel:
![]()
Dalam hal ini fungsi tersebut memiliki tiga variabel dan dua fungsi skalar, sehingga matriks Jacobian akan menjadi matriks persegi panjang berdimensi 2×3:
![Rendered by QuickLaTeX.com \displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5b327537a2e4c80c7eb38d56d94bb141_l3.png)
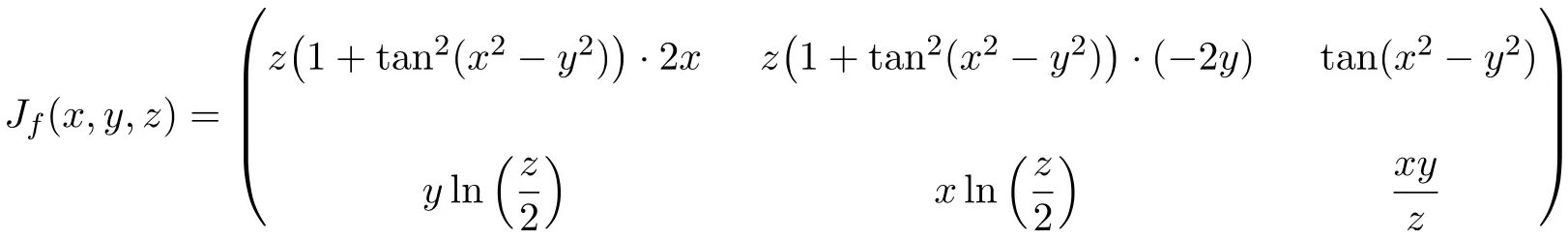
Setelah kita mendapatkan ekspresi matriks Jacobian, kita evaluasinya pada titik (2,-2,2):
![Rendered by QuickLaTeX.com \displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a62dd1b4655e9d089404028ec48fbe11_l3.png)
Kami melakukan perhitungan:
![Rendered by QuickLaTeX.com \displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-05c8aaa8cca0f4cb652c95b11d2e9db1_l3.png)
Dan kami terus beroperasi hingga tidak dapat disederhanakan lagi:
![Rendered by QuickLaTeX.com \displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2b4fda9837a6287456ca469d46a2382_l3.png)
Latihan 4
Tentukan matriks Jacobian pada titik tersebut
![]()
dari fungsi multivariabel berikut:
![]()
Dalam hal ini fungsi tersebut memiliki dua variabel dan tiga fungsi skalar, sehingga matriks Jacobian akan menjadi matriks persegi panjang berdimensi 3×2:
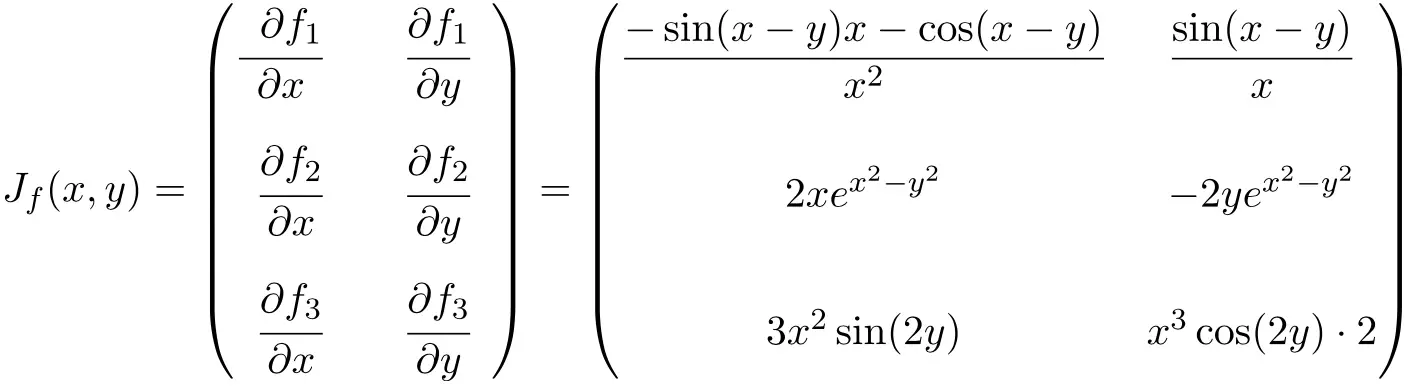
Setelah kita mendapatkan ekspresi untuk matriks Jacobian, kita mengevaluasinya secara langsung
![]()
![Rendered by QuickLaTeX.com \displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-167caa7a7d1cb34db33f7b92e21b5f78_l3.png)
Kami melakukan operasi:
![Rendered by QuickLaTeX.com \displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b05c5bfee3f874f3adec324a6bc9b43e_l3.png)
Dengan demikian matriks Jacobian dari fungsi vektor pada titik yang dipertimbangkan bernilai:
![Rendered by QuickLaTeX.com \displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4addee61e4664b95dbb049be217af34_l3.png)
Latihan 5
Hitung matriks Jacobian pada titik tersebut
![]()
dari fungsi berikut dengan 3 variabel:
![]()
Dalam hal ini fungsinya terdiri dari tiga variabel dan tiga fungsi skalar, sehingga matriks Jacobian akan berupa matriks persegi berdimensi 3×3:
![Rendered by QuickLaTeX.com \displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd9dcbb1d4961906d5b8581f70f5392_l3.png)
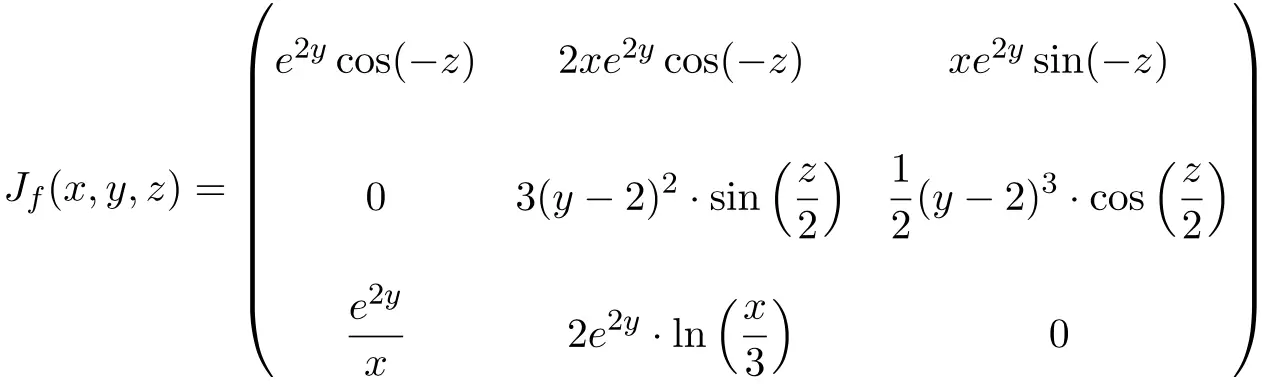
Setelah kami menemukan matriks Jacobian, kami mengevaluasinya pada saat itu juga
![]()
![Rendered by QuickLaTeX.com \displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4f56df32b7632d1e74f014f0aab2b52a_l3.png)
Kami menghitung operasi:
![Rendered by QuickLaTeX.com \displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5771c5e1c54eabf6df6633abd5f3e194_l3.png)
Dan hasil matriks Jacobian pada titik tersebut adalah:
![Rendered by QuickLaTeX.com \displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6dc1884b96ce985e1475c5cfcba2fff8_l3.png)
Penentu matriks Jacobian: Jacobian
Penentu matriks Jacobian disebut determinan Jacobian atau Jacobian. Harus diingat bahwa Jacobian hanya dapat dihitung jika fungsi tersebut memiliki jumlah variabel yang sama dengan fungsi skalar, karena matriks Jacobian akan memiliki jumlah baris yang sama dengan kolom dan oleh karena itu akan berbentuk persegi. matriks. .
Contoh Jacobian
Mari kita lihat contoh penghitungan determinan Jacobian suatu fungsi dengan dua variabel:
![]()
Pertama-tama kita menghitung matriks Jacobian dari fungsi tersebut:
![Rendered by QuickLaTeX.com \displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5870e75f368ea3e554b2fa32cfa554dc_l3.png)
Dan sekarang kita selesaikan determinan matriks 2×2:
![Rendered by QuickLaTeX.com \displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d1ef9df1d4735e3cea235c653714439_l3.png)
Jacobian dan invertibilitas suatu fungsi
Sekarang setelah Anda melihat konsep Jacobian, Anda mungkin berpikir… apa gunanya?
Nah, kegunaan utama dari Jacobian adalah untuk menentukan apakah suatu fungsi dapat dibalik. Teorema fungsi invers menyatakan bahwa jika determinan matriks Jacobian (Jacobian) berbeda dengan 0, berarti fungsi tersebut dapat dibalik.
![]()
Perlu diperhatikan bahwa kondisi ini perlu tetapi tidak cukup, yaitu jika determinannya bukan nol maka kita dapat menyatakan bahwa matriksnya dapat dibalik, namun jika determinannya 0 maka kita tidak dapat mengetahui apakah matriks tersebut. fungsi memiliki invers atau No.
Misalnya, dalam contoh yang terlihat sebelumnya tentang cara mencari Jacobian suatu fungsi, determinannya diberikan
![]()
. Dalam hal ini kita dapat menyatakan bahwa fungsi tersebut selalu dapat dibalik kecuali pada titik (0,0), karena titik ini adalah satu-satunya titik yang determinan Jacobiannya sama dengan nol dan, oleh karena itu, kita tidak mengetahui apakah invers fungsinya ada pada titik ini.
Hubungan matriks Jacobian dengan operasi lain
Matriks Jacobian berhubungan dengan gradien dan matriks Hessian suatu fungsi:
Lereng
Jika fungsinya merupakan fungsi skalar, maka matriks Jacobian akan berupa matriks baris yang ekuivalen dengan gradien :
![]()
![]()
Matriks Goni
Matriks Jacobian dari gradien suatu fungsi sama dengan matriks Hessian :
![]()
Matriks Hessian merupakan matriks yang sangat penting untuk menurunkan fungsi dengan lebih dari satu variabel, karena matriks tersebut dibentuk oleh turunan kedua dari fungsi tersebut. Bahkan, bisa dikatakan matriks Hessian merupakan kesinambungan dari matriks Jacobian. Namun sangat penting bagi kita untuk memiliki satu halaman penuh yang menjelaskannya secara detail. Jadi jika Anda ingin mengetahui secara pasti apa itu matriks dan mengapa begitu istimewa, Anda bisa mengklik link tersebut.
Penerapan matriks Jacobian
Selain kegunaan Jacobian yang telah kita lihat, yang menentukan apakah suatu fungsi dapat dibalik, matriks Jacobian memiliki penerapan lain.
Matriks Jacobian digunakan untuk menghitung titik kritis suatu fungsi multivariat, yang kemudian diklasifikasikan menjadi titik maxima, minima atau saddle melalui matriks Hessian. Untuk menemukan titik kritis, Anda perlu menghitung matriks Jacobian dari fungsi tersebut, menetapkannya sama dengan 0, dan menyelesaikan persamaan yang dihasilkan.
![]()
Selain itu, penerapan lain dari matriks Jacobian terdapat pada integrasi fungsi dengan lebih dari satu variabel, yaitu pada integral rangkap, integral rangkap tiga, dan sebagainya. Karena determinan matriks Jacobian memungkinkan perubahan variabel dalam integral berganda sesuai dengan rumus berikut:
![]()
![]()
Dimana T adalah fungsi perubahan variabel yang menghubungkan variabel awal dengan variabel baru.
Terakhir, matriks Jacobian juga digunakan untuk membuat pendekatan linier terhadap fungsi apa pun
![]()
sekitar suatu titik
![]()
:
![]()