Di halaman ini Anda akan menemukan rumus kuadrat suatu jumlah, yaitu identitas penting (a+b) 2 . Anda juga akan dapat melihat contoh dan latihan soal jumlah kuadrat. Dan terlebih lagi, Anda akan menemukan sifat geometris yang tersembunyi dalam produk luar biasa ini.
Berapa kuadrat suatu jumlah?
Kuadrat suatu jumlah adalah salah satu identitas penting (atau hasil kali penting), jadi ini adalah aturan matematika yang memungkinkan Anda dengan cepat menghitung pangkat binomial dengan dua suku positif kuadrat.
Jadi, kuadrat suatu jumlah terdiri dari dua suku berbeda yang dijumlahkan dan dikuadratkan, sehingga ekspresi aljabar kuadrat suatu jumlah adalah (a+b) 2 .
Rumus kuadrat suatu jumlah
Mengingat definisi matematis dari jenis identitas yang luar biasa ini, sekarang kita akan melihat apa rumus kuadrat suatu jumlah :

Sehingga kuadrat suatu jumlah sama dengan kuadrat suku pertama, ditambah dua kali hasil kali suku pertama dan suku kedua, ditambah kuadrat suku kedua.
Jadi, untuk menyelesaikan penjumlahan kuadrat, tidak cukup dengan menaikkan setiap penjumlahan menjadi dua, tetapi, selain itu, kedua penjumlahan tersebut harus dikalikan dengan 2.
Hal ini penting untuk diingat, karena kesalahan yang sangat umum saat menjumlahkan kuadrat adalah melupakan hasil kali antara kedua suku dan hanya menghitung kuadratnya:

Ingatlah untuk tidak menghilangkan suku apa pun dari rumus!
Di sisi lain, ingatlah bahwa rumus pengurangan kuadrat (atau kuadrat pengurangan) sangat mirip dengan yang baru saja kita lihat, namun memiliki perbedaan yang mengubah hasilnya sepenuhnya. Jika Anda tidak yakin seperti apa rumusnya, Anda dapat memeriksa di sini apa itu rumus pengurangan kuadrat dan cara penerapannya.
Contoh jumlah kuadrat
Berikut adalah beberapa contoh praktis sehingga Anda dapat mengetahui cara mengkuadratkan suatu jumlah:
Contoh 1
- Hitung jumlah kuadrat berikut dengan menerapkan rumus:
![]()
Rumus jumlah kuadrat adalah:
![]()
Pertama-tama kita harus mengidentifikasi parameternya
![]()
Dan
![]()
dari rumus tersebut. Pada kasus ini,
![]()
mewakili
![]()
dari pasangan dan
![]()
sesuai dengan nomor 5:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
Nah, karena sekarang kita sudah mengetahui nilai-nilainya
![]()
dan dari
![]()
Kita dapat menerapkan rumus untuk mencari hasil kuadrat dari jumlah tersebut:

Contoh 2
- Selesaikan persamaan berikut untuk kuadrat suatu jumlah:
![]()
Rumus kuadrat suatu jumlah adalah:
![]()
Jadi dalam masalah ini
![]()
adalah monomial
![]()
Dan di sisi lain,
![]()
adalah istilah independen 4:
![Rendered by QuickLaTeX.com \begin{array}{c} a=3x \\[2ex] b=4 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-89bb3514fbd79ba368588655e152e9cc_l3.png)
Akhirnya, setelah kita mengidentifikasi nilai-nilai
![]()
dan dari
![]()
, kami menerapkan rumus jumlah kuadrat untuk menyelesaikan produk penting:
![Rendered by QuickLaTeX.com \begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ed0d9fcdbeeac2247b68789dd0268f37_l3.png)
Bukti rumus kuadrat suatu jumlah
Kemudian kita akan menyimpulkan rumus yang baru saja kita lihat dari kuadrat suatu jumlah, sehingga Anda mengerti dari mana asalnya.
Mulai dari binomial positif dipangkatkan menjadi 2:
![]()
Kekuatan di atas jelas setara dengan faktornya
![]()
dikalikan dengan dirinya sendiri:
![]()
Jadi, kita mengalikan kedua tanda kurung menggunakan sifat distributif:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
Terakhir, dari suku-suku yang dihasilkan, kami mengelompokkan suku-suku yang serupa:
![]()
Dan kita sudah sampai pada ekspresi polinomial rumusnya, sehingga terbukti:
![]()
Meskipun sulit dipercaya, rumus jumlah kuadrat juga dapat digunakan untuk memfaktorkan polinomial kuadrat . Jika Anda belum tahu apa itu, pemfaktoran polinomial adalah prosedur yang sering digunakan dalam matematika untuk menyederhanakan ekspresi polinomial. Cari tahu cara melakukannya dengan mengeklik tautan di atas.
Interpretasi geometris dari kuadrat suatu jumlah
Sejauh ini kita telah melihat bagaimana kuadrat suatu jumlah dihitung secara matematis, namun hasil kali yang luar biasa ini juga dapat diinterpretasikan secara geometris.
Perhatikan persegi berikut yang sisi-sisinya diukur
![]()
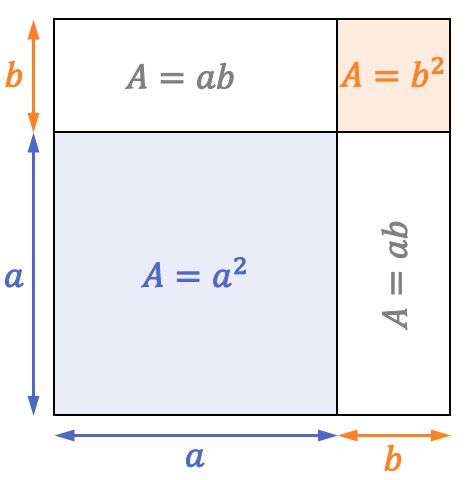
Luas persegi sama dengan kuadrat panjang salah satu sisinya. Oleh karena itu, seperti sisi persegi sebelumnya
![]()
luasnya (atau permukaannya) sama dengan
![]()
Seperti yang Anda lihat pada representasi persegi, persegi dengan luas
![]()
persegi panjang dengan dua luas
![]()
dan permukaan persegi lainnya
![]()
Oleh karena itu, rumus jumlah persegi juga terpenuhi dari sudut pandang geometri:
![]()
Memecahkan masalah kuadrat suatu jumlah
Kemudian kami meninggalkan Anda dengan beberapa latihan jumlah kuadrat yang diselesaikan langkah demi langkah sehingga Anda dapat berlatih dan menyelesaikan pemahaman konsepnya. Anda dapat menulis semua pertanyaan Anda kepada kami di komentar, dan kami akan dengan senang hati menjawabnya. 💭💭💭
Latihan 1
Tentukan jumlah kuadrat berikut:
![]()
![]()
![]()
![]()
Untuk menyelesaikan semua identitas penting dari masalah tersebut, cukup menerapkan rumus kuadrat suatu jumlah:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d696f9e8ea8a9246922a0aa132d7e24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
Latihan 2
Selesaikan jumlah kuadrat dua suku berikut dengan menerapkan rumus:
![]()
![]()
![]()
Untuk menghitung semua produk penting dari soal tersebut, Anda harus menggunakan rumus jumlah kuadrat:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8eaa03c68adc376819c5e12081f6d39_l3.png)
Di bagian B) Anda perlu mengingat bahwa jika suatu akar dikuadratkan, maka disederhanakan:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a38b1df7ca331cb002253d52eb008608_l3.png)
Monomial dari jumlah kuadrat terakhir mempunyai koefisien pecahan, jadi untuk menyelesaikannya kita juga perlu menggunakan sifat-sifat pecahan:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
Latihan 3
Temukan pangkat berikut dengan menerapkan rumus kuadrat suatu jumlah dan tanpa menggunakan kalkulator:
![]()
Pertama-tama, angka tujuh belas dapat dipecah menjadi jumlah 10 ditambah 7:
![]()
Jadi kami mengubah pangkatnya menjadi jumlah kuadrat. Oleh karena itu, sekarang kita dapat menerapkan rumus yang sesuai:
![Rendered by QuickLaTeX.com \begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e35048f0ae6ae12bc2b5b3d761fb99_l3.png)
Singkatnya, hasil potensiasi adalah:
![]()
Seperti yang Anda lihat di latihan ini, rumus jumlah kuadrat juga berguna untuk menghitung pangkat bilangan besar tanpa menggunakan kalkulator.
Kuadrat dari jumlah 3 suku
Terkadang kita mungkin perlu menyelesaikan kuadrat tiga suku yang dijumlahkan, yaitu (a+b+c) 2 . Logikanya, dalam kasus ini kita tidak bisa menggunakan rumus yang telah kita jelaskan, karena di dalam tanda kurung kita mempunyai trinomial, bukan binomial. Oleh karena itu perlu menggunakan formula yang berbeda.
Rumus kuadrat jumlah 3 suku adalah sebagai berikut:
![]()
Mari kita lihat bagaimana rumus ini diterapkan melalui sebuah contoh:
![Rendered by QuickLaTeX.com \begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0816bbe156553fc1ef5920ac2b2e09f_l3.png)
Seperti yang Anda lihat, menambahkan satu elemen ke rumus akan membuat hasilnya jauh lebih rumit.