Pada artikel ini, Anda akan mempelajari cara menurunkan arctangen suatu fungsi. Selain itu, Anda akan dapat melihat contoh turunan jenis ini dan bahkan berlatih dengan latihan yang diselesaikan pada turunan tangen busur. Terakhir, kami juga tunjukkan bukti rumus turunan tangen busur.
Apa turunan dari garis singgung busur?
Turunan dari garis singgung busur x adalah satu per satu ditambah x kuadrat.
![]()
Oleh karena itu, turunan tangen suatu fungsi sama dengan hasil bagi turunan fungsi tersebut dibagi satu ditambah kuadrat fungsi tersebut.
![]()
Dalam hal ini, fungsi tersebut diwakili oleh au, jadi ini akan menjadi rumus turunan dari tangen busur fungsi u.
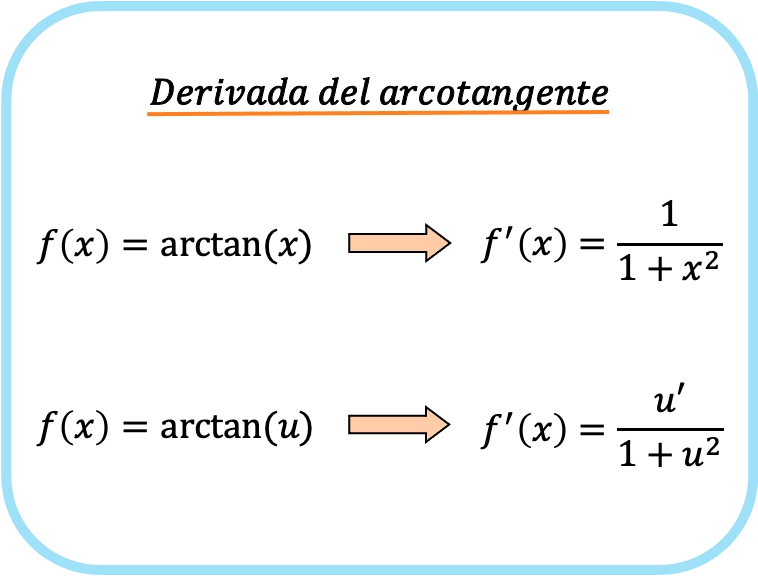
Seperti yang Anda lihat, rumus turunan invers tangen sangat mirip dengan rumus turunan arcsinus dan arccosine.
Contoh turunan dari arctangent
Setelah kita mengetahui rumus turunan tangen busur, kami akan menjelaskan turunan dari beberapa contoh turunan trigonometri jenis ini. Dengan cara ini, Anda akan lebih mudah memahami cara menurunkan arctangen suatu fungsi.
Contoh 1: Turunan dari arctangen 2x
![]()
Kami menerapkan rumus untuk menyelesaikan turunannya:
![]()
Turunan dari 2x adalah 2, jadi turunan arctangen dari 2x adalah 2 per satu ditambah 2x kuadrat:
![]()
Contoh 2: Turunan dari arctangen x kuadrat
![]()
Untuk mencari hasil turunan dari contoh ini, kita perlu menggunakan rumus turunan tangen busur, yaitu:
![]()
Jadi, turunan fungsi x 2 adalah 2x, maka turunan tangen busur x yang dipangkatkan 2 adalah:
![]()
Contoh 3: Turunan dari arctangen sinus x
![]()
Logikanya, untuk menghitung turunannya Anda harus menerapkan rumus yang sesuai:
![]()
Dalam hal ini kita mempunyai fungsi komposit, jadi kita harus menerapkan aturan rantai untuk menghitung turunan dari tangen busur:
![]()
Latihan soal turunan dari garis singgung busur
Turunkan fungsi arctangen berikut:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Demonstrasi rumus turunan garis singgung busur
Selanjutnya kita akan membuktikan rumus turunan tangen busur.
![]()
Pertama-tama kita ubah garis singgung busur menjadi garis singgung dengan memanfaatkan fakta bahwa garis singgung busur adalah fungsi kebalikan dari garis singgung:
![]()
Kami membedakan kedua sisi persamaan:
![]()
Kami menghapus dan’:
![]()
Di sisi lain, berkat identitas trigonometri dasar kita mengetahui bahwa jumlah kuadrat sinus dan kosinus sama dengan 1. Oleh karena itu, kita dapat mengubah ekspresi sebelumnya menjadi pecahan:
![]()
![]()
Kami membagi semua suku dengan kuadrat kosinus:
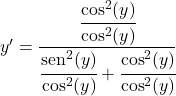
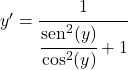
Sinus dibagi cosinus sama dengan garis singgung, jadi:
![]()
![]()
Seperti yang kita lihat di atas, garis singgung setara dengan variabel x, oleh karena itu kita dapat mensubstitusikan persamaan tersebut untuk mendapatkan rumus turunan dari garis singgung busur:
![]()