Matriks kesatuan

Pada halaman ini kami menjelaskan apa itu matriks kesatuan dan juga kami ilustrasikan dengan beberapa latihan agar dapat dipahami dengan baik. Anda juga akan menemukan sifat-sifat matriks jenis ini yang sangat penting untuk aljabar linier.

Apa itu matriks kesatuan?

Pengertian matriks kesatuan adalah sebagai berikut:

Matriks kesatuan adalah matriks kompleks yang dikalikan matriks transpos konjugasinya sama dengan matriks identitas. Artinya, kondisi berikut terpenuhi:

U\cdot U^* = U^* \cdot U =I

Emas

U

adalah matriks kesatuan dan

U^*

transpos terkonjugasinya.

Oleh karena itu, kondisi ini menyiratkan bahwa invers suatu matriks satuan adalah transpos konjugasinya , karena menurut definisi invers matriks, suatu matriks adalah invers dari matriks lain jika hasil kali matriks tersebut ekuivalen dengan matriks d’identifikasi .

\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}

Oleh karena itu, matriks kesatuan akan selalu merupakan matriks beraturan atau matriks tak berdegenerasi , karena matriks tersebut selalu mempunyai invers.

Sebaliknya, analogi matriks kesatuan dalam lingkungan bilangan real adalah matriks ortogonal , dan dalam hal ini benar bahwa matriks kesatuan dikalikan transposnya sama dengan matriks identitas.

U\cdot U^t = U^t \cdot U =I

Jadi dalam hal ini matriks invers dari U akan langsung menjadi matriks yang ditransposisikan (atau ditransposisikan).

Contoh matriks satuan

Contoh matriks satuan berdimensi 2×2

Setelah kita melihat konsep matriks satuan, kita akan melihat contoh matriks satuan 2×2 agar dapat memahaminya dengan baik:

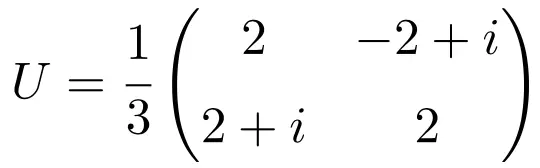
contoh matriks satuan berdimensi 2x2

Matriks ini bersifat kesatuan karena perkalian dirinya dengan matriks konjugasinya menghasilkan matriks Identitas (atau Satuan):

\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

Dan, seperti yang kita lihat sebelumnya, setiap matriks kesatuan dapat diubah dengan transpos konjugasinya:

\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

Contoh Matriks Diagonal Satuan

Matriks diagonal yang hanya terdiri dari bilangan kompleks i juga merupakan contoh matriks kesatuan, berapapun dimensi matriksnya. Di bawah ini Anda memiliki latihan terselesaikan yang mengilustrasikannya dengan matriks satuan berdimensi 3 × 3:

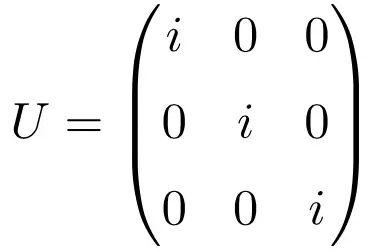
contoh matriks satuan berdimensi 3x3

Perhatikan bahwa jika kita menyelesaikan hasil kali matriks dengan transpos konjugasinya, maka matriks Identitas akan dihasilkan sebagai solusinya:

\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

Hal yang sama terjadi jika kita mengalikan matriks secara terbalik:

\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

Ciri-ciri matriks ini adalah sebagai contoh matriks kesatuan berdimensi sembarang, karena setiap kali matriks tersebut dibentuk oleh bilangan imajiner i pada diagonal utama dan elemen-elemen lainnya adalah nol (0 ) itu akan menjadi matriks kesatuan.

Sifat-sifat matriks kesatuan

Sifat-sifat matriks satuan adalah sebagai berikut:

  • Jelasnya, setiap matriks kesatuan adalah matriks normal . Meskipun tidak semua matriks normal merupakan matriks kesatuan.
  • Semua matriks satuan dapat didiagonalisasi, yaitu dapat diubah menjadi matriks diagonal.
  • Nilai absolut determinan suatu matriks satuan selalu sama dengan 1.

\begin{vmatrix} det(U) \end{vmatrix} = 1

  • untuk semua

    n

    , himpunan semua matriks satuan

    n\times n

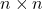
    dengan operasi perkalian matriks, mereka membentuk suatu kelompok yang disebut kelompok satuan.

  • Sehingga perkalian dua matriks satuan yang berordo sama menghasilkan matriks satuan yang lain.
  • Modulus semua nilai eigen (atau nilai eigen) suatu matriks satuan selalu sama dengan 1.

\begin{vmatrix} \lambda \end{vmatrix} = 1

  • Ruang eigen matriks jenis ini bersifat ortogonal.

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top