Pada halaman ini kami menjelaskan apa itu segitiga Tartaglia atau disebut juga segitiga Pascal. Kita belajar bagaimana membangun segitiga Tartaglia (atau Pascal) secara matematis, serta kegunaannya dan semua propertinya. Terakhir, kami menunjukkan bagaimana dan kapan segitiga yang sangat penting ini terbentuk.
Apa segitiga Tartaglia (atau Pascal)?
Segitiga Tartaglia , disebut juga segitiga Pascal , adalah representasi matematis dari bilangan bulat terurut dalam bentuk segitiga. Segitiga Tartaglia (atau Pascal) digunakan untuk melakukan perhitungan matematis.
Inilah pengertian segitiga Tartaglia atau Pascal, namun Anda pasti lebih memahami konsepnya dengan gambar segitiga:
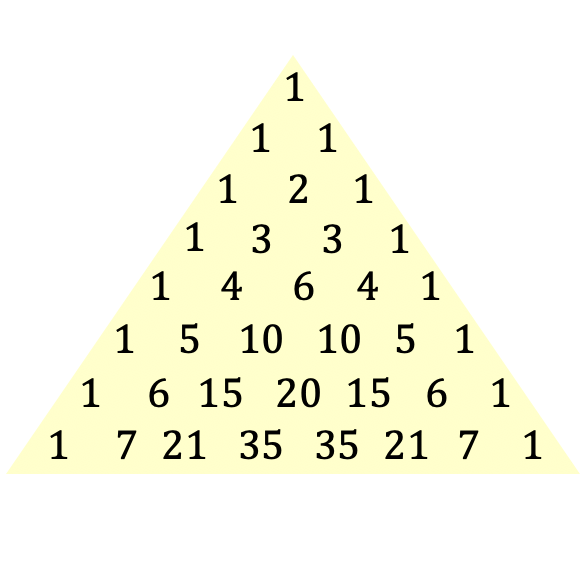
Segitiga Tartaglia disebut juga segitiga Pascal setelah filsuf dan matematikawan Perancis Blaise Pascal, yang memperkenalkan ungkapan segitiga ini pada tahun 1654, meskipun segitiga ini sudah dikenal sejak zaman dahulu. Di bawah ini kita akan mempelajari sejarah segitiga khusus ini.
Bagaimana segitiga Tartaglia atau Pascal dibangun?
Seperti yang Anda lihat pada segitiga Pascal (atau Tartaglia), angkanya banyak sekali, tapi bukan berarti kita harus hafal (syukurlah). Ada rumus yang memudahkan Anda mencari semua bilangan pada segitiga Pascal atau Tartaglia, Anda hanya perlu menyelesaikan penjumlahan sederhana.
Untuk membuat segitiga Tartaglia atau Pascal, Anda mulai dari puncak segitiga, yang selalu bernilai 1, lalu garis-garis di bawahnya dihitung. Setiap bilangan pada baris berikut merupakan penjumlahan dua bilangan yang berada tepat di atasnya, kecuali ujung-ujung garis selalu 1.

Oleh karena itu, Anda dapat menghitung garis segitiga Tartaglia sebanyak yang Anda inginkan, karena Anda dapat menjumlahkan garis secara berurutan dengan menjumlahkan angka-angkanya.
Segitiga Tartaglia atau Pascal digunakan untuk apa?
Mengetahui cara membuat segitiga Tartaglia memang sangat bagus, tapi… untuk apa segitiga aritmatika ini digunakan? Nah, segitiga Tartaglia (atau Pascal) memiliki banyak penerapan dalam matematika, khususnya dalam bidang aljabar.
bilangan kombinatorial
Pertama-tama, segitiga Tartaglia digunakan untuk menghitung bilangan kombinatorial secara langsung, disebut juga koefisien binomial. Jika Anda tidak tahu apa jenis operasi ini, Anda dapat mencarinya di situs web kami (kami memiliki mesin pencari di kanan atas) karena kami telah menulis artikel terperinci di mana kami menjelaskan cara penyelesaiannya dan Anda di sana. juga akan menemukan contoh dan latihan yang diselesaikan langkah demi langkah. Namun secara ringkas, ekspresi aljabar suatu bilangan kombinatorial adalah sebagai berikut:
![]()
Nah, semua bilangan kombinatorial dapat dengan mudah ditentukan dengan segitiga Tartaglia, karena solusi setiap koefisien binomial setara dengan bilangan ekspresi segitiga ini seperti yang ditunjukkan pada gambar berikut:

Misalnya bilangan kombinatorial
![]()
mengembalikan 6, karena di segitiga Tartaglia ada 6 sebagai gantinya.
Jadi, jika Anda mengetahui cara membuat segitiga Tartaglia atau Pascal, Anda dapat menghitung bilangan kombinatorial apa pun dengan cepat dan tanpa menggunakan rumusnya.
binomial Newton
Kegunaan lain dari segitiga Tartaglia (atau Pascal) adalah untuk menghitung pangkat binomial (klik tautan ini untuk mengetahui apa itu binomial).
Contoh potensiasi binomial adalah identitas penting, seperti:
![]()
Identitas yang luar biasa sangat penting bagi matematika, karena identitas memungkinkan kita menyimpan banyak perhitungan dan menyelesaikan operasi rumit secara langsung dan cepat. Itu sebabnya kami menyarankan untuk memeriksa tautan berikut jika Anda masih belum tahu apa itu Identitas Terkemuka .
Seperti yang Anda lihat di tautan sebelumnya, produk terkenal dapat diselesaikan langsung dengan rumusnya. Tapi… apa yang terjadi jika pasangan dinaikkan ke kubus atau ke derajat yang lebih tinggi?
![Rendered by QuickLaTeX.com \begin{array}{c} (a+b)^3 = \ ? \\[3ex] (a+b)^4 = \ ? \\[3ex] (a+b)^5 = \ ? \\[3ex] \bm{\vdots} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5b0a3cca7974eff9ac7a93f3178897c5_l3.png)
Nah, binomial ini dapat dihitung dengan cara yang sangat sederhana menggunakan segitiga Tartaglia berkat teorema binomial (atau binomial Newton). Sekali Meskipun menguasai metode ini, penerapannya cepat, untuk menjelaskannya dengan baik Anda memerlukan satu halaman penuh. Jadi jika Anda lebih tertarik dengan cara menyelesaikan binomial jenis ini, klik halaman tertaut dan Anda dapat melihat cara melakukannya.
Kombinatorik
Segitiga Tartaglia, atau segitiga Pascal, juga dapat digunakan untuk menentukan kombinasi dan probabilitas.
Jika kita pernah menghadapi masalah di mana kita perlu menentukan berapa banyak kelompok berbeda yang dapat dibuat dari suatu kelompok tanpa menghiraukan urutannya, kita dapat menggunakan segitiga Tartaglia.
Misal kita punya 5 kartu, untuk mengetahui berapa banyak cara kita bisa memilih 3, langsung saja ke kolom ketiga (kolom pertama nol) baris kelima (baris pertama juga baris 0) segitiga Tartaglia. Angka pada posisi ini (10) sesuai dengan banyaknya kemungkinan untuk memilih 3 kartu.
![]()
Jadi, dari 5 kartu dapat dibentuk 10 kelompok berbeda yang terdiri dari tiga kartu.
Sifat-sifat segitiga Tartaglia atau Pascal
Segitiga Tartaglia disebut juga segitiga Pascal memiliki ciri-ciri sebagai berikut:
- Segitiga Tartaglia (atau Pascal) adalah simetris, yaitu garis vertikal yang membagi seluruh segitiga menjadi dua segitiga sama sisi yang sama merupakan sumbu simetri.
- Jumlah horizontal semua bilangan pada setiap garis segitiga Pascal sama dengan pangkat 2.

- Diagonal segitiga Tartaglia juga penting: bilangan pada diagonal pertama (diagonal luar) adalah satu, diagonal kedua dibentuk oleh barisan semua bilangan asli, diagonal ketiga sesuai dengan bilangan segitiga, dan diagonal keempat terdiri dari bilangan tetragonal (atau tetrahedral).
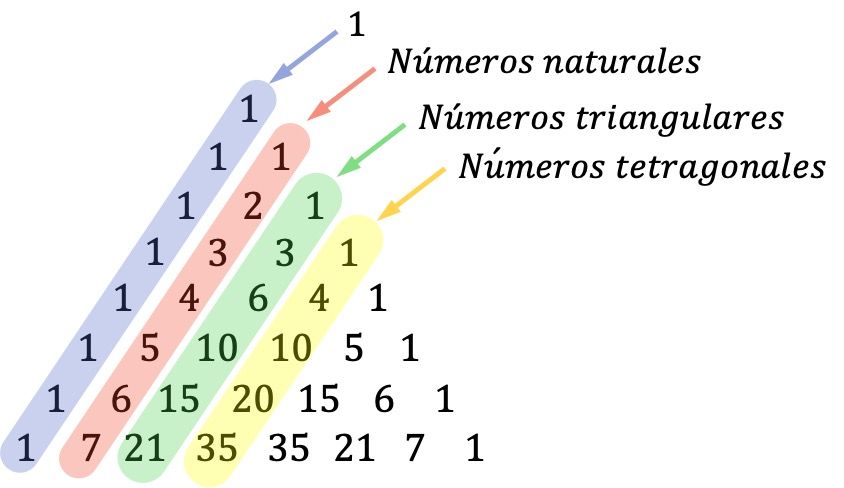
Bilangan segitiga adalah bilangan yang dapat direpresentasikan dalam bentuk segitiga. Dan bilangan tetragonal adalah bilangan yang membentuk limas segitiga.
Kalau belum tahu apa itu bilangan segitiga atau tetragonal, tidak terjadi apa-apa, yang ada hanya rasa penasaran tentang segitiga Tartaglia. Namun, Anda perlu mengetahui pengertian bilangan asli (bilangan yang digunakan untuk menghitung unsur).
- Kecuali bilangan 1, jika bilangan pertama pada suatu garis adalah bilangan prima, maka semua bilangan pada garis yang sama habis dibagi bilangan tersebut. Misalnya pada baris kedelapan (1-7-21-35-35-21-7-1), angka 7, 21 dan 35 dapat dibagi 7 (tujuh adalah bilangan prima).
- Keunikan lain dari segitiga Tartaglia adalah deret Fibonacci dapat dicari dengan menjumlahkan diagonal-diagonalnya dengan cara tertentu:
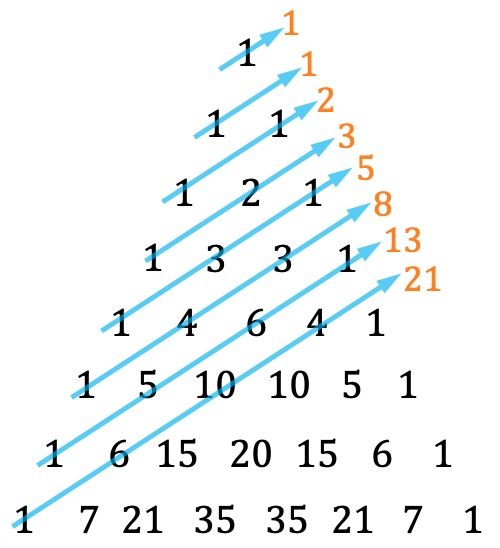
Ingatlah bahwa setiap suku deret Fibonacci sama dengan jumlah dua suku sebelumnya, dua suku pertama adalah 1 dan 1. Jadi bilangan-bilangan yang termasuk dalam deret Fibonacci adalah: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144, 233,…
- Jika kita menjumlahkan dua bilangan berurutan dari diagonal ketiga segitiga Pascal (1-3-6-10-15-…) kita memperoleh kuadrat sempurna (1, 4, 9, 16, 25,…).
- Jika kita melukis bilangan genap segitiga Pascal dengan satu warna dan bilangan ganjil dengan warna lain, kita memperoleh bangun segitiga Sierpinski, suatu himpunan geometri yang terkenal. Di bawah ini Anda dapat melihat segitiga Pascal dengan tinggi 512 yang diwakili dengan bilangan ganjil berwarna hitam dan bilangan genap berwarna putih:

- Dugaan Singmaster mengatakan bahwa berapa kali setiap angka yang lebih besar dari 1 muncul adalah berhingga. Atau dengan kata lain, walaupun jumlah baris pada segitiga Tartaglia tidak terhingga, namun banyaknya kemunculan setiap bilangan kecuali 1 adalah berhingga. Yang membuat penasaran, angka 3003 adalah satu-satunya angka yang diketahui hingga saat ini muncul hingga delapan kali dalam segitiga.
Sejarah segitiga Tartaglia atau Pascal
Sekarang setelah kita mengetahui seperti apa bentuk segitiga Tartaglia, mari kita lihat kapan segitiga matematika yang sangat istimewa ini ditemukan.
Meskipun nama segitiga aritmatika terutama diberikan kepada ilmuwan terkenal Tartaglia dan Pascal, segitiga aljabar ini sudah digunakan sebelumnya.
Catatan pertama tentang segitiga yang dibentuk oleh koefisien binomial berasal dari abad ke-10 di India. Namun bangsa Persia mulai mempelajari sifat-sifatnya, terutama ahli matematika Al-Karaji (953-1029) dan Omar Khayyam (1048-1131). Inilah sebabnya di Iran dipopulerkan sebagai segitiga Khayyam-Pascal atau bahkan sekadar segitiga Khayyam .
Segitiga ini mulai diperkenalkan ke Tiongkok pada abad ke-11 oleh ahli matematika Jia Xian, namun kemudian pada abad ke-13 Yang Hui memperkenalkannya sebagai segitiga aritmatika . Dan karena itulah, di negara Asia mereka menyebutnya segitiga Yang Hui .
Segitiga matematika mencapai benua Eropa kemudian melalui Petrus Apianus dari Jerman, yang secara khusus diterbitkan pada tahun 1527 dalam bukunya Rechnung . Dari sana, ahli aljabar Italia terkenal Niccolò Fontana Tartaglia mempelajari segitiga secara mendalam selama paruh pertama abad ke-16, dan untuk menghormatinya di negara-negara seperti Italia dikenal sebagai segitiga Tartaglia.
Akhirnya, orang Prancis Blaise Pascal mendemonstrasikan banyak sifat-sifat segitiga yang dipelajari dalam publikasinya Risalah tentang Segitiga Aritmatika pada tahun 1654, oleh karena itu dinamakan segitiga Pascal. Perlu dicatat bahwa beberapa sifat ini telah diketahui, tetapi Pascal-lah yang mendemonstrasikannya dengan induksi matematika.